La desigualdad triangular o desigualdad de Minkowski es un teorema de geometría euclidiana que establece:
Este resultado ha sido generalizado a otros contextos más sofisticados como espacios vectoriales. Definido matemáticamente, cualquier triángulo cumple la siguiente propiedad:
donde a, b y c son los lados.
Desigualdad del triángulo.
Espacios vectoriales normados
El teorema puede generalizarse a espacios vectoriales normados, obteniéndose la siguiente versión de la desigualdad triangular:
|
Es decir, que La norma de la suma de dos vectores es siempre menor o igual a la suma de las normas de los dos vectores.
En el caso particular de considerar la recta real como espacio vectorial normado con el valor absoluto como norma obtenemos la siguiente versión del teorema:
|
cuya demostración es:
Demostración
(Ámbito → ℝ). Haciendo uso de las propiedades del valor absoluto, es posible escribir:
Sumando ambas inecuaciones:
A su vez, usando la propiedad de valor absoluto 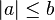 si y solo si
si y solo si  en la línea de arriba queda:
en la línea de arriba queda:
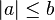 si y solo si
si y solo si  en la línea de arriba queda:
en la línea de arriba queda:Generalización de la desigualdad triangular
La desigualdad triangular puede generalizarse a un número arbitrario de sumandos:
,
es decir:
donde n es un número natural, y los  son números reales.
son números reales.
 son números reales.
son números reales.| Demostración |
Esta desigualdad puede generalizarse aún más para integrales (Riemann, Riemann-Stieltjes, Lebesgue-Stieltjes, etc):
así como también para espacios Lp. Sea S un espacio medible, sea 1 ≤ p ≤ ∞ y sea f y g elementos de Lp(S). Entonces f + g es de Lp(S), y se tiene
con la igualdad para el caso1 < p < ∞ si y sólo si f y g son positivamente linealmente dependientes (que significa que f = λg o g = λf para algún λ ≥ 0).
Igual que la desigualdad de Hölder, la desigualdad de Minkowski se puede especificar para sucesiones y vectores haciendo:
para todos los números reales (o complejos) x1, ..., xn, y1, ..., yn y donde n es el cardinal de S (el número de elementos de S).
Es fácil comprobar por qué sucede eso. Imagina que quieres ir del punto amarillo al azul. Si vas siguiendo la línea recta recorrerás una longitud "a", mientras que si vas pasando por el punto rojo recorrerás una longitud "b+c". Pero sabemos que el camino más corto entre dos puntos es la línea recta, así que "b+c" tiene que ser mayor que "a":
b + c > a
Lo mismo pasará si queremos ir del punto amarillo al rojo (a+b>c) o del azul al rojo (a+c>b).
Desigualdad triangular
En todo triángulo la suma de las longitudes de dos lados cualquiera es siempre mayor a la longitud del lado restante.
Este hecho es una consecuencia de otro teorema de la geometría plana clásica que afirma que la distancia más corta entre dos puntos es la línea recta.
Esto quiere decir que las medidas de los lados de un triángulo no pueden ser cualesquiera. Practica con la siguiente animación interactiva para comprobar esto.
Desigualdad triangular
Para cualesquiera x,y números reales tenemos que
| x + y | ≤ | x | + | y |
Para cualesquiera x,y números reales tenemos que
| x + y | ≤ | x | + | y |
Es llamada de tal manera debido a que la suma de las longitudes de dos lados cualesquiera de un triángulo siempre es menor que la longitud del otro lado.
Observa que la desigualdad es estricta en el caso que se tengan números de signos contrarios
Signos contrarios
|(–3) + 4 | = | 1 | < |–3 | + | 4 | = 7
Desigualdad estricta
Del mismo signo
| (–3) + (–6) | = | –9 | = 9 = |–3 | + | -6 | = 9
Se alcanza la igualdad
| 6 + 5 | = | 11 | = 11 = | 6 | + | 5 |
Se alcanza la igualdad
Un número igual a 0
| –6 + 0 |=|–6 | = 6 = | –6 | + | 0 |
Se alcanza la igualdad


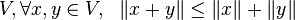

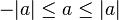





No hay comentarios:
Publicar un comentario