polinomios de Bernoulli 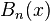 se definen mediante la función generatriz:
se definen mediante la función generatriz:
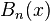 se definen mediante la función generatriz:
se definen mediante la función generatriz:
Aparecen en el estudio de numerosas funciones especiales, en particular de la función zeta de Riemann y de la función zeta de Hurwitz. Los números de Bernoulli  son los términos independientes de los polinomios correspondientes, i.e.,
son los términos independientes de los polinomios correspondientes, i.e.,  .
.
 son los términos independientes de los polinomios correspondientes, i.e.,
son los términos independientes de los polinomios correspondientes, i.e.,  .
.
La identidad  nos permite dar una forma cerrada de la suma
nos permite dar una forma cerrada de la suma
 nos permite dar una forma cerrada de la suma
nos permite dar una forma cerrada de la suma
Expresión explícita de polinomios de menor grado






 .
.- números y polinomios de Bernoulli.Enunciado1. Se considera una sucesión de números reales llamados números de Bernoullidefinidos de la formaCalcular para Demostrar que es racional para todo
Solución. 1. Usando la relación de recurrencia dada, obtenemos - Un binomio es un polinomio que consta de dos monomios.P(x) = 2x2 + 3x
Binomio al cuadrado
Un binomio al cuadrado es igual es igual al cuadrado del primer término más, o menos, el doble producto del primero por el segundo más el cuadrado segundo.(a + b)2 = a2 + 2 · a · b + b2(x + 3)2 = x 2 + 2 · x ·3 + 3 2 = x 2 + 6 x + 9(a − b)2 = a2 − 2 · a · b + b2(2x - 3)2 = (2x)2 + 2 · 2x · 3 + 3 2 = 4x2 + 12 x + 9Binomio al cubo
Un binomio al cubo es igual al cubo del primero más, o menos, el triple del cuadrado del primero por el segundo más el triple del primero por el cuadrado del segundo más, o menos, el cubo del segundo.(a + b)3 = a3 + 3 · a2 · b + 3 · a · b2 + b3(x + 3)3 = x 3 + 3 · x2 · 3 + 3 · x· 32 + 33 == x 3 + 9x2 + 27x + 27(a − b)3 = a3 − 3 · a2 · b + 3 · a · b2 − b3(2x - 3)3 = (2x)3 - 3 · (2x)2 ·3 + 3 · 2x· 32 - 33 == 8x 3 - 36 x2 + 54 x - 27Diferencia de cuadrados
Una diferencia de cuadrados es igual a una suma por diferencia.a2 − b2 = (a + b) · (a − b)4x2 − 25 = (2x)2 − 52 = (2x + 5) · (2x - 5)Suma de cubos
a3 + b3 = (a + b) · (a2 − ab + b2)8x3 + 27 = (2x + 3) (4x2 - 6x + 9)Diferencia de cubos
a3 − b3 = (a − b) · (a2 + ab + b2)8x3 − 27 = (2x − 3) (4x2 + 6x + 9)Producto de dos binomios que tienen un término común
(x + a) (x + b) = x2 + ( a + b) x + ab(x + 2) (x + 3) == x2 + (2 + 3)x + 2 · 3 == x2 + 5x + 6Binomio de Newton
La fórmula que nos permite hallar las potencias de un binomio se conoce como binomio de Newton.Podemos observar que:El número de términos es n+1.Los coeficientes son números combinatorios que corresponden a la fila enésima del triángulo de Tartaglia.En el desarrollo del binomio los exponentes de a van disminuyendo, de uno en uno, de n a cero; y los exponentes de b van aumentando, de uno en uno, de cero a n, de tal manera que la suma de los exponentes de a y de b en cada término es igual a n.En el caso que uno de los términos del binomio sea negativo, se alternan los signos positivos y negativos.

 .
. .
. es una diferencia de expresiones trigonométricas.
es una diferencia de expresiones trigonométricas.



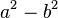 puede factorizarse como el producto de dos binomios:
puede factorizarse como el producto de dos binomios: .
.
 .
.
 es:
es: .
.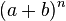 , y puede desarrollarse utilizando la fórmula de
, y puede desarrollarse utilizando la fórmula de 

 .
.
 , se conoce como
, se conoce como 


 , se desarrolla el binomio
, se desarrolla el binomio  . El
. El  que es
que es  es la derivada de
es la derivada de  . Obsérvese que si consideramos el trinomio del desarrollo como dependiente de
. Obsérvese que si consideramos el trinomio del desarrollo como dependiente de  .
.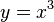 se desarrolla
se desarrolla  . En el cuatrinomio resultante, el coeficiente de
. En el cuatrinomio resultante, el coeficiente de 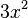 , que es la derivada de
, que es la derivada de  .
.
No hay comentarios:
Publicar un comentario