polinomio ciclotómico de orden n y se denota como Φn al polinomio unitario cuyas raíces son todas las raíces primitivas de orden n de la unidad, es decir, que verifican zn = 1 .
Se suele tomar las raíces en el cuerpo de los complejos, (otras extensiones del cuerpo de los reales serían posibles), pero carece de consecuencia sobre los polinomios ciclotómicos, cuyos coeficientes son siempre enteros. El grado de Φn es dado por la función φ de Euler, y es lógicamente inferior o igual a n.
Las raíces primitivas son de la forma ωr, con 0 ≤ r < n, r coprimo con n, y  . Entonces
. Entonces
 . Entonces
. EntoncesHistoria
Nacimiento de la noción
Carl Friedrich Gauss utiliza en sus Disquisitiones Arithmeticae, publicado en 1801, los polinomios ciclotómicos. Se hace una importante contribución a un problema abierto desde la antigüedad: la construcción con regla y compás de polígonos regulares. Estos trabajos sirven de referencia a lo largo del siglo. En este trabajo, Gauss determina con precisión la lista de polígonos construibles, y le da un método eficaz para su construcción hasta 256 lados del polígono. Este problema recibe una respuesta final por Pierre- Laurent Wantzel (1814 - 1848) en un artículo1 en adelante célebre.
Este enfoque es innovador y, en muchos aspectos, prefigura álgebra moderna: Un polinomio ya no aparece como un objeto en sí mismo, sino como parte de un conjunto estructurado. Si el concepto del anillo de polinomios no se formaliza, la estructura euclidiana se encuentra y es la herramienta básica para el análisis de Gauss.
La resolución efectiva de la ecuación de Gauss ciclotómico llevó a considerar una estructura finita: las permutaciones de las raíces. Ahora se llaman periodo de Gauss. Sus propiedades algebraicas se utilizan para encontrar la solución. Este enfoque prevé el uso de la teoría de grupos en el álgebra y la teoría de Galois.
Las nuevas estructuras se definen a continuación. La división euclidiana introduce la noción de residuo y su conjunto tiene propiedades algebraicas fuertes. Tal estructura ahora se considera un caso especial de la finita si el divisor es un número primo. Gauss resalta tales conjuntos y utiliza el transporte de estructura para morfismos entre dos anillos para mostrar la irreductibilidad de polinomios ciclotómicos. En el mismo libro, él utiliza estas estructuras para resolver otro problema abordado por Fermat (1601 - 1685) y formalizado por Euler (1707 - 1783): la ley de reciprocidad cuadrática.
Por este tiempo, se proponen muchas aplicaciones. La utilización de la geometría no se limita a la construcción con la regla y el compás. El polinomio ciclotómico de índice cuatro permite la construcción de un nuevo conjunto de números algebraicos el de los enteros de Gauss. Una rama de la matemática surge: la teoría de números algebraicos, que simplifica la resolución de ecuaciones diofánticas y permite resolver nuevos.
Ecuación polinómica y algebraica ciclotómicos
La búsqueda de soluciones a la ecuación polinómica es un problema que se remonta a los primeros desarrollos en polinomios por los matemáticos árabes. Aunque en general se cita a Al- Khwarizmi ( 783-850 ) como precursor con la resolución de seis ecuaciones canónicas, Girolamo Cardano ( 1501-1576 ) para la resolución del caso de grado tres y Ludovico Ferrari ( 1522-1565 ) para el cuarto. El caso general continuó siendo durante mucho tiempo misterioso. Joseph - Louis Lagrange (1736 - 1813) incluye la resolución de este problema general está íntimamente relacionado con las propiedades de las permutaciones de raíces. El caso especial de los polinomios ciclotómicos lo muestra. El grupo de permutaciones buenas, ahora llamado grupo de Galois, no solo es conmutativa sino además cíclica. Esta propiedad, que se utiliza en torno al concepto de períodos de Gauss, permite una eficaz solución para este caso particular. Un análisis más profundo Ruffini Paolo ( 1765-1822 ), Niels Henrik Abel ( 1802-1829 ) y sobre todo por Evariste Galois ( 1811-1832 ) muestra que el aspecto conmutativa del grupo es, de hecho, una condición suficiente. Para ser precisos, la situación indica que el grupo debe ser dividido en una serie de grupos conmutativos anidadas. La pregunta natural que surge es determinar las extensiones del cuerpo de los números racionales cuyo grupo de Galois es conmutativa. Estas extensiones se llaman extensiones abelianas. La estructura del cuerpo asociado con el polinomio ciclotómico extensión llamada ciclotómico, es un ejemplo. Que sea única significa que toda ecuación algebraica resoluble por radicales se reduce de una manera u otra a un polinomio ciclotómico. La respuesta es que toda extensión abeliana del cuerpo de los racionales es un subcuerpo de una extensión ciclotómico. La prueba de este resultado ha necesitado casi medio siglo esfuerzo para terminar de ser demostrado. Los principales científicos para dicha demostración fueron Leopold Kronecker (1823 - 1891) y Heinrich Weber ( 1842-1913 ). Si el análisis de las extensiones abelianas finitas termina con el siglo XIX, se deja abierta una amplia gama de cuestiones, por ejemplo en aritmética. Parece necesario generalizar la noción de campo ciclotómico sobre extensiones infinitas. La cuestión la plantea David Hilbert ( 1862-1943 ).2 Esta investigación se llama la teoría de las clases de cuerpo. Esta teoría es uno de los más exitosos en el siglo XX. Se puede citar por ejemplo el teorema de reciprocidad3 de Emil Artin ( 1998-62 ) que resuelve el noveno de los problemas de Hilbert, o más recientemente, dos laureados de la medalla Fields para sus trabajos sobre generalizaciones de la teoría: Vladimir Drinfeld1990 o Laurent Lafforgue en 2002.
Propiedades
- El grado del n-ésimo polinomio ciclotómico viene dado por la función φ de Euler:
 .
.
En particular, siempre será menor o igual a n.
 , el polinomio ciclotómico
, el polinomio ciclotómico  es de coeficientes enteros, es decir,
es de coeficientes enteros, es decir, ![\Phi_n(X) \in \mathbb{Z}[X]](https://upload.wikimedia.org/math/1/5/e/15e37354f6ebe225ee09f30601e8276d.png) .
.
 , el polinomio ciclotómico
, el polinomio ciclotómico ![\Phi_n(X) \in \mathbb{Z}[X]](https://upload.wikimedia.org/math/1/5/e/15e37354f6ebe225ee09f30601e8276d.png) , es irreducible en
, es irreducible en ![\mathbb{Z}[X]](https://upload.wikimedia.org/math/8/9/4/8948f9796109cbb4f99d4dd5ba0b3b82.png) y en
y en ![\mathbb{Q}[X]](https://upload.wikimedia.org/math/1/2/e/12e7b267ca89f819cb51e1e108ba6678.png) .
.
 p primo,
p primo,  tal que p no divide n, y
tal que p no divide n, y  , se tiene:
, se tiene: 
 n impar, se tiene:
n impar, se tiene: 
 primo y
primo y  tal que p no divide n, se tiene:
tal que p no divide n, se tiene: 
Cálculo de los polinomios ciclotómicos
El polinomio  tiene por raíces todas las raíces n-ésimas de la unidad y toda raíz n-ésima de la unidad es raíz d-ésima primitiva para algún divisor d de n; de la misma manera, las raíces de
tiene por raíces todas las raíces n-ésimas de la unidad y toda raíz n-ésima de la unidad es raíz d-ésima primitiva para algún divisor d de n; de la misma manera, las raíces de  , para d divisor de n también son raíces de
, para d divisor de n también son raíces de  . Se deduce pues la siguiente igualdad:
. Se deduce pues la siguiente igualdad:
 tiene por raíces todas las raíces n-ésimas de la unidad y toda raíz n-ésima de la unidad es raíz d-ésima primitiva para algún divisor d de n; de la misma manera, las raíces de
tiene por raíces todas las raíces n-ésimas de la unidad y toda raíz n-ésima de la unidad es raíz d-ésima primitiva para algún divisor d de n; de la misma manera, las raíces de  , para d divisor de n también son raíces de
, para d divisor de n también son raíces de  . Se deduce pues la siguiente igualdad:
. Se deduce pues la siguiente igualdad:
Mediante esta última, encontramos una primera manera recursiva de calcular los polinomios ciclotómicos:
Si queremos calcular el polinomio ciclotómico p-ésimo, donde p es un número primo, como p no es divisible por ningún número menor que él distinto de 1, todas las raíces de la unidad exceptuando el uno son raíces primitivas, por tanto:
Utilizando la función de Möbius, se obtiene otra manera no recursiva de calcular los polinomios ciclotómicos:
Ejemplos
Calculemos los polinomios ciclotómicos de orden 2 y 3, al ser ambos números primos su cálculo es inmediato:
Ahora mediante las fórmulas anteriores y teniendo en cuenta que  , calculamos los polinomios de orden mayor:
, calculamos los polinomios de orden mayor:
 , calculamos los polinomios de orden mayor:
, calculamos los polinomios de orden mayor:
Calculemos ahora algunos polinomios ciclotómicos usando la función de Möbius
Ejemplos gráficos
En la imagen tenemos por un lado las raíces duodécimas de la unidad de  y las raíces séptimas por otro. De esta manera:
y las raíces séptimas por otro. De esta manera:
 y las raíces séptimas por otro. De esta manera:
y las raíces séptimas por otro. De esta manera:- si n=12: las raíces primitivas són las
 , con k=1,5,7,11 ya que solo para estos valores de k tenemos: mcd(12,k)=1.
, con k=1,5,7,11 ya que solo para estos valores de k tenemos: mcd(12,k)=1.
- si n=7: las raíces primitivas són las
 , con k=1,2,3,4,5,6 ya que 7 és un número primo y por lo tanto todos los k cumplen: mcd(7,k)=1.
, con k=1,2,3,4,5,6 ya que 7 és un número primo y por lo tanto todos los k cumplen: mcd(7,k)=1.
Cuerpos ciclotómicos
Una de las aplicaciones de los polinomios ciclotómicos es en el contexto del álgebra, cuando se usa para construir cuerpos ciclotómicos. Sean K un cuerpo algebraicamente cerrado y k un subcuerpo de éste. Consideremos ![f(X) \in k[X]](https://upload.wikimedia.org/math/3/8/5/385ddec8c5df2b865050d939d8d81cc1.png) un polinomio irreducible y
un polinomio irreducible y  una raíz de
una raíz de  . Resulta que
. Resulta que ![k(\theta) \simeq k[X]/(f(X))](https://upload.wikimedia.org/math/7/6/d/76d0c209b9e1295e32fa17a30045b25b.png) de manera que
de manera que ![[k(\theta): k]= \operatorname{gr}(f(X))](https://upload.wikimedia.org/math/e/f/f/eff4dfc6d556c3eb048b559aca867f69.png) , es decir, el grado del polinomio
, es decir, el grado del polinomio  será el grado de extensión
será el grado de extensión  sobre k que es el mínimo cuerpo que contiene k y
sobre k que es el mínimo cuerpo que contiene k y  .
.
![f(X) \in k[X]](https://upload.wikimedia.org/math/3/8/5/385ddec8c5df2b865050d939d8d81cc1.png) un polinomio irreducible y
un polinomio irreducible y  una raíz de
una raíz de  . Resulta que
. Resulta que ![k(\theta) \simeq k[X]/(f(X))](https://upload.wikimedia.org/math/7/6/d/76d0c209b9e1295e32fa17a30045b25b.png) de manera que
de manera que ![[k(\theta): k]= \operatorname{gr}(f(X))](https://upload.wikimedia.org/math/e/f/f/eff4dfc6d556c3eb048b559aca867f69.png) , es decir, el grado del polinomio
, es decir, el grado del polinomio  será el grado de extensión
será el grado de extensión  sobre k que es el mínimo cuerpo que contiene k y
sobre k que es el mínimo cuerpo que contiene k y  .
.
Consideremos ahora, 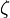 una raíz n-ésima primitiva de la unidad. Entonces tendremos que
una raíz n-ésima primitiva de la unidad. Entonces tendremos que ![[\mathbf{Q}(\zeta) : \mathbf{Q}] =\operatorname{gr}(\Phi_n(X)) = \varphi(n)](https://upload.wikimedia.org/math/2/d/b/2dbc02b72ad1c9ecfcff25bd839d9abf.png) , y, como en la generalización, tendremos que el grado de la extensión del cuerpo de los racionales junto a la raíz primitiva n-ésima será el grado del polinomio ciclotómico n-ésimo.
, y, como en la generalización, tendremos que el grado de la extensión del cuerpo de los racionales junto a la raíz primitiva n-ésima será el grado del polinomio ciclotómico n-ésimo.
Por otro lado, también es importante remarcar el resultado siguiente: Sean 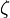 una raíz n-ésima primitiva de la unidad. Entonces tendremos que
una raíz n-ésima primitiva de la unidad. Entonces tendremos que ![[\mathbf{Q}(\zeta) : \mathbf{Q}] =\operatorname{gr}(\Phi_n(X)) = \varphi(n)](https://upload.wikimedia.org/math/2/d/b/2dbc02b72ad1c9ecfcff25bd839d9abf.png) , y, como en la generalización, tendremos que el grado de la extensión del cuerpo de los racionales junto a la raíz primitiva n-ésima será el grado del polinomio ciclotómico n-ésimo.
, y, como en la generalización, tendremos que el grado de la extensión del cuerpo de los racionales junto a la raíz primitiva n-ésima será el grado del polinomio ciclotómico n-ésimo. números naturales primos entre sí. Entonces, el producto de las dos raíces primitivas
números naturales primos entre sí. Entonces, el producto de las dos raíces primitivas  es una raíz mn-ésima primitiva de la unidad y se satisfacen las igualdades:
es una raíz mn-ésima primitiva de la unidad y se satisfacen las igualdades:  y
y  .
.CARACTERIZACIÓN DE LOS FACTORES PRIMOS DE LOS POLINOMIOS CICLOTÓMICOS
RESUMEN
El resultado principal de este trabajo está relacionado con otros recogidos en varios artículos escritos para analizar la estructura de los factores primos de ciertas expresiones numéricas, entre ellos el titulado “Caracterización de los factores de la suma de dos números elevados a la misma potencia” [1] ya que como demostraremos, los polinomios ciclotómicos pueden dedcirse como factores de la suma de dos números enteros elevados a una misma potencia.
DESARROLLO
Resulta fácil imaginar que algunas de las cuestiones que pueden plantearse en el estudio de tales números están directamente relacionadas con el teorema de Fermat – Wiles, cuyo celebérrimo enunciado no vamos a transcribir aquí por razones obvias, aunque si recordamos que tiene que ver con números de la forma:an ± bn
Para los que sabemos que, cuando n es un número impar, podemos escribir:
Y cuando el exponente es un número primo, p, tenemos:
Según se demuestra en [1], todos los factores de la anterior expresión son de la forma dada en (1) salvo en los casos en los que (a ± b) sea múltiplo de p, para los que hay que tener en cuenta que hemos de añadir un factor p a la descomposición.
Definición
Por otro lado, de acuerdo con los textos académicos sobre teoría algebraica y teoría de números, se denomina polinomio ciclotómico de orden n y se denota como Fn al polinomio unitario cuyas raíces son todas las raíces primitivas de orden n de la unidad, es decir, que verifican zn = 1.
El polinomio ciclotómico n-ésimo está definido, según eso, por el hecho de que sus ceros son precisamente las raíces primitivas n-ésimas de la unidad, cada una con multiplicidad 1:
donde z1,...,zΦ(n) son las raíces primitivas n-ésimas de la unidad, yΦ(n) es la función de Euler.
El polinomio Fn(z) tiene coeficientes enteros y es un polinomio irreducible sobre el cuerpo de los números racionales, lo que significa que no puede ser escrito como producto de dos polinomios de grado positivo con coeficientes racionales.
Podemos recordar que cada raíz n-ésima de la unidad es cualquiera de los n números complejos distintos que son raíces del polinomio:zn - 1
Y que dicha raíz n-ésima es una raíz primitiva d-ésima de la unidad para algún entero d tal que1 ≤ d ≤ n
Lo cual implica que:
Fórmula que representa la factorización del polinomio zn - 1 en factores irreducibles.
Los polinomios ciclotómicos pueden calcularse recursivamente a partir de la relación (2) y mediante la inversión de Möbius podemos obtener:
Donde μ es la función de Möbius definida por
Con lo que los primeros polinomios ciclotómicos son:
De la relación anterior puede verse que cuando el grado del polinomio ciclotómico es un número primo, tenemos que:
Y así mismo, resulta fácil ver que para todo n impar se verifica:
Veamos ahora cómo podemos obtener a partir de lo expuesto la factorización del polinomio zn + 1 . Sabemos que se cumple:
Y a partir de ahí:
Así, por ejemplo:
Para obtener la factorización de expresiones de la forma:an ± bn
A partir de lo visto, podemos hacer:
Para factorizar el término entre paréntesis como ya sabemos por los resultados anteriores.
EJEMPLO NUMERICO
Como ejemplo numérico vamos a obtener la descomposición en factores primos del número:1315 + 215
En primer lugar, vemos que 13 + 2 = 15 y, evidentemente dicho valor es múltiplo del exponente o, lo que es igual, de cada uno de los factores que lo componen; de ese modo, ya sabemos que en la descomposición factorial vamos a tener los factores 32 y 52.
Así:
Y de ese modo:
Con lo cual:
Y podemos comprobar, de acuerdo con los resultados teóricos, que los factores primos distintos de 3 y 5, deducibles de las partes exponenciales, son respectivamente de la forma:


























No hay comentarios:
Publicar un comentario