AMIGOS PARA SIEMPRE: Polinomios

función polinómica es una función asociada a un polinomio con coeficientes en un anillo conmutativo (a menudo un cuerpo).

Formalmente, es una función:

f:x \mapsto P(x)\,

donde

P(x)\,

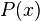es un polinomio definido para todo número real

x\,

; es decir, una suma finita de potencias de

x\,

multiplicados por coeficientes reales, de la forma:¹

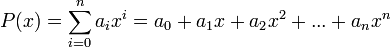
P(x) = \sum_{i=0}^n a_i x^i = a_0+a_1x+a_2x^2+...+a_nx^n

Otra definición

Si p(x) es un polinomio en la variable x entonces decimos que esta es una función polinomial p : R → R que asigna a cada punto x ∈ R el valor p(x) ∈ R.

Funciones polinómicas básicas

Algunas funciones polinómicas reciben un nombre especial según el grado del polinomio:

Grado	Nombre	Expresión
0	función constante	y = a
1	función lineal	y = ax + b es un binomio del primer grado
2	función cuadrática	y = ax² + bx + c es un trinomio del segundo grado
3	función cúbica	y = ax³ + bx² + cx + d es un cuatrinomio de tercer grado

Función polinómica

Enunciado

Las funciones polinómicas de primer grado se denominan funciones afines y son funciones del tipo f(x) =a x + b.
Su gráfica es una recta con pendiente "a" y que pasa por el punto (0,b). Al número "b" se le llama ordenada en el origen.
Las funciones polinómicas de segundo grado se denominan funciones cuadráticas, y son funciones del tipo f(x) = a x² + b x + c, con a≠0.
Su gráfica es una parábola.

Con la ayuda de la aplicación, intenta dibujar distintas funciones variando los valores de los parámetros de la función:

f(x)= a x⁴ + b x³ + c x² + d x + e

Qué hacer

Moviendo los deslizadores de color verde, podemos cambiar el valor de los coeficientes de la función polinómica:

f(x)= a x⁴ + b x³ + c x² + d x + e.

Para mover los deslizadores con facilidad y precisión, puedes hacer clic sobre ellos y pulsar las teclas de flecha o las teclas + y -

En la barra de herramientas puedes desplazar los ejes

, hacer zoom para acercar

o para alejar

la vista gráfica.

Para calcular f(x₀), la imagen del valor x₀, desplaza el punto azul A sobre el eje de abcisas.

Los puntos amarillos sobre la gráfica son los extremos relativos: máximos y mínimos de la función.

Para volver a la posición inicial haz clic en

Preguntas

1. La función f está definida como f(x)= x⁴ - 2 x³ - 3 x² + 3 x + 4.

a. Calcula la imagen para x₀=2

b. ¿Cuánto vale la ordenada en el origen?

c. Para qué valor de x₀, la imagen vale -2.

d. Si f(x₀)=1, ¿cuánto vale x₀?

2. El dominio de las funciones polinómicas es ¡, por lo que podemos calcular la imagen para cualquier valor real. El recorrido de la función es el conjunto de valores que toma la función. Determina el recorrido para las siguientes funciones:

a. f(x)= x⁴ - 2 x³ - 3 x² + 3 x + 4

b. f(x)= 2 x³ - 3 x² + 3 x + 4

c. f(x)= x² - 2 x + 3

d. f(x)= x-1

e. Investiga la relación del recorrido de la función polinómica con el grado del polinomio.

3. Las funciones afínes son funciones polinómicas de grado 1, del tipo: f(x) = m x +n.

Para este ejercicio establece los valores a=0, b=0 , c=0, d=3 y e=4.

a. ¿Cómo es la gráfica de la función?

b. ¿Cuánto vale la pendiente y la ordenada en el origen?

c. Describe lo que sucede a la grafica de f al variar el coeficiente de primer grado. Cómo debe ser la pendiente para que la función sea decreciente.

d. Describe lo que sucede a la gráfica de f al variar el coeficiente independiente. ¿Por qué punto pasa siempre si la ordenada en el origen es 0?

4. Las funciones cuadráticas son funciones polinómicas de grado 2, del tipo: f(x) = a x² + b x + c.

Para este ejercicio establece los valores a=0, b=0, c=1, d=-2 y e=-3.

a. ¿Cómo es la gráfica de la función?

b. Determina los intervalos de crecimiento y decrecimiento de la función f.

c. En qué valor tiene su vértice. ¿Es máximo o mínimo?

d. Establece los coeficientes de primer grado e independientes a 0. Describe que le sucede a la gráfica de la función f al variar el coeficiente de segundo grado.

e. Establece el coeficiente de segundo grado a 1 y el de primer grado a 0. Describe que le sucede a la gráfica de la función f al variar el coeficiente independiente. ¿Dónde se encuentra el vértice?

f. Investiga cuál es la expresión algebraica de la función cuadrática que corta el eje de abcisas en x₁=0 y x₂=2.

5. Para este ejercicio establece los valores iniciales, a=1, b=-2, c=-3, d=3 y e=4

a. Determina los intervalos de crecimiento y decrecimiento de la función f.

b. En qué puntos se encuentran los máximos y mínimos.

c. Describe que le sucede a la gráfica de la función f al variar el coeficiente independiente.

d. Investiga cuántos puntos máximos y mínimos puede tener la función polinómica.

6. Una función es cóncava en un punto si la recta tangente a la gráfica en ese punto está por debajo de la gráfica. Y es cónvexa en un punto si la recta tangente a la gráfica en ese punto está por encima de la gráfica. El punto donde se produce el cambio de concavidad a convexidad se llama punto de inflexión.

Para este ejercicio establece los valores iniciales, a=1, b=-2, c=-3, d=3 y e=4.

a. Determina los intervalos de concavidad y convexidad.

b. Investiga cuantos puntos de inflexión tiene la función polinómica.

7. La gráfica de una función cúbica, (función polinómica de grado 3) es una curva que presenta una simetría central respecto de un punto de la curva, el punto de inflexión.

Para este ejercicio establece el valor de a=0, así la función polinómica será de grado 3.

a. Investiga cuantos puntos de inflexión tiene la función cúbica.

funciones simétricas monomiales son una clase especial de funciones simétricas que forman la base más simple del espacio vectorial de funciones simétricas.

Definición

\lambda=(\lambda_1,\lambda_2,\ldots,\lambda_n)

es una partición, se construye el monomio

$x^\lambda = x_1^{\lambda_1}x_2^{\lambda_2}\cdots x_n^{\lambda_n}$ .

La suma de tales monomios sobre todas las permutaciones distintas de

\lambda

, da como resultado un polinomio simétrico denotado

m_\lambda\,

(Función simétrica monomial) La función simétrica monomial asociada a la partición $\lambda\vdash n$ es la suma

$m_\lambda=\sum_\sigma x^\sigma\,$ ,

donde $\sigma$ recorre todas las permutaciones distintas de $\lambda$ .

Ejemplos

Las funciones simétricas monomiales en cuatro variables para las particiones más pequeñas son:

$m_\emptyset = 1$ .
$m_1 = x_1 + x_2 + x_3 + x_4\,$ .
$m_2 = x_1^2 + x_2^2 + x_3^2 + x_4^2$ .
$m_{11} = x_1x_2 + x_1x_3 + x_1x_4+x_2x_3+x_2x_4 + x_3x_4\,$ .
$m_3 = x_1^3 + x_2^3 + x_3^3 +x_4^3$ .
$m_{21} = x_1^2x_2 + x_2^2x_1^1 + x_1^2x_3 + x_3^2x_1 + x_1^2x_4 +x_4^2x_1 + x_2^2x_3 + x_3^2x_2 + x_2^2x_4 + x_4^2x_2 + x_3^2x_4+x_4^2x_3$ .

Obsérvese que en

m_{11}

sólo aparece

x_1x_3

y no

x_3x_1

, porque ambas corresponden a la misma permutación

(1 0 1 0)

de la partición

(1 1 0 0)

. En particular, se consideran todas las particiones de un entero

n

como si tuvieran

n

partes, añadiendo entradas cero de ser necesario.

Propiedades

Cualquier función simétrica en n variables

$f(x_1,x_2,\ldots,x_n)=\sum_\sigma x^\sigma$

puede reescribirse en términos de funciones simétricas monomiales como

$f(x_1,x_2,\ldots,x_n)=\sum_{\lambda} m_\lambda$ ,

por lo que el conjunto de funciones simétricas monomiales indizadas por las particiones de n

$\{ m_\lambda : \lambda \vdash n \}$

forma una base del espacio vectorial

\Lambda_n

de funciones simétricas en n variables.

Una consecuencia de la relación anterior es el siguiente teorema.

La dimensión del espacio vectorial $\Lambda_n$ sobre $\mathbb{Q}$ de funciones simétricas en n variables es igual al número $p(n)$ de particiones del entero n, y el conjunto de funciones simétricas monomiales es una base de dicho espacio vectorial.