interpolación de Hermite, nombrada así en honor a Charles Hermite, es un método de interpolación de puntos de datos como una función polinómica. El polinomio de Hermite generado está estrechamente relacionado con el polinomio de Newton, en tanto que ambos se derivan del cálculo de diferencias divididas.
Consiste en buscar un polinomio por pedazos 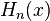 que sea cúbico en cada subintervalo
que sea cúbico en cada subintervalo ![[x_{(i-1)},x_i], 1 \leq i \le n](https://upload.wikimedia.org/math/4/f/2/4f20f811bafa2eec743b499bd8f4980e.png) y que cumpla
y que cumpla  en los puntos
en los puntos  , donde
, donde  es la función que se quiere interpolar.
es la función que se quiere interpolar.
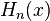 que sea cúbico en cada subintervalo
que sea cúbico en cada subintervalo ![[x_{(i-1)},x_i], 1 \leq i \le n](https://upload.wikimedia.org/math/4/f/2/4f20f811bafa2eec743b499bd8f4980e.png) y que cumpla
y que cumpla  en los puntos
en los puntos  , donde
, donde  es la función que se quiere interpolar.
es la función que se quiere interpolar.
La función 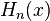 queda determinada en forma única por estas condiciones y su cálculo requiere de la solución de
queda determinada en forma única por estas condiciones y su cálculo requiere de la solución de  sistemas lineales de ecuaciones de tamaño
sistemas lineales de ecuaciones de tamaño  cada uno.
cada uno.
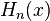 queda determinada en forma única por estas condiciones y su cálculo requiere de la solución de
queda determinada en forma única por estas condiciones y su cálculo requiere de la solución de  sistemas lineales de ecuaciones de tamaño
sistemas lineales de ecuaciones de tamaño  cada uno.
cada uno.
La desventaja de la interpolación de Hermite es que requiere de la disponibilidad de los  lo cual no es el caso en muchas aplicaciones.
lo cual no es el caso en muchas aplicaciones.
 lo cual no es el caso en muchas aplicaciones.
lo cual no es el caso en muchas aplicaciones.Uso
Ejemplo
Considerada la función  , evaluando la función y sus primeras dos derivadas en
, evaluando la función y sus primeras dos derivadas en  , se obtienen los siguientes datos:
, se obtienen los siguientes datos:
 , evaluando la función y sus primeras dos derivadas en
, evaluando la función y sus primeras dos derivadas en  , se obtienen los siguientes datos:
, se obtienen los siguientes datos:x ƒ(x) ƒ'(x) ƒ''(x) −1 2 −8 56 0 1 0 0 1 2 8 56
Puesto que tenemos dos derivadas para trabajar, construiremos el conjunto  . Nuestra tabla de diferencias divididas es entonces:
. Nuestra tabla de diferencias divididas es entonces:
 . Nuestra tabla de diferencias divididas es entonces:
. Nuestra tabla de diferencias divididas es entonces:
y el polinomio generado es
mediante la adopción de los coeficientes de la diagonal de la tabla de diferencia dividida, y multiplicando el k-ésimo coeficiente por  , como lo haríamos al generar un polinomio de Newton.
, como lo haríamos al generar un polinomio de Newton.
 , como lo haríamos al generar un polinomio de Newton.
, como lo haríamos al generar un polinomio de Newton.
El polinomio de Hermite es aquel que interpola una colección de puntos y el valor de sus derivadas en los puntos que deseamos. Es decir, supongamos que tenemos (xk,fk) y (xk,f′k) .
Entonces construimos la misma tabla que en el método de Newton, poniendo en la primera columna los xk , escribiendo dos veces el mismo punto si conocemos el valor de la derivada en ese punto, y en la segunda columna los valores de f correspondiente al x e la misma fila. Es decir, si conocemos el valor de f en x0 y el de su derivada también, escribiremos dos veces x0 y al lado de cada uno f0 . Por ejemplo,
A partir de aquí procedemos de la misma forma, pero con la diferencia que tenemos que definir f[xi,xi]=f′i , el valor de la derivada en xi .
Por lo tanto, si disponemos de n+1 valores de la función y n+1 valores de las derivadas, el polinomio de Hermite tendrá grado 2n+1 .
Consideremos un ejemplo:
Ejemplo
Supongamos que queremos calcular f(18) donde f(x)=tan(πx) a partir de interpolación de Hermite en 0,14 .
Para conseguirlo, escribimos una tabla como en interpolación de Newton pero repitiendo cada dato del que conozcamos su derivada. Es decir:
Procediendo de la misma forma que en interpolación de Newton, obtenemos:
Ahora,
![\begin{matrix}
z_0 = -1 & f[z_0] = 2 & & & & & & & & \\
& & \frac{f'(z_0)}{1} = -8 & & & & & & & \\
z_1 = -1 & f[z_1] = 2 & & \frac{f''(z_1)}{2} = 28 & & & & & & \\
& & \frac{f'(z_1)}{1} = -8 & & f[z_3,z_2,z_1,z_0] = -21 & & & & & \\
z_2 = -1 & f[z_2] = 2 & & f[z_3,z_2,z_1] = 7 & & 15 & & & & \\
& & f[z_3,z_2] = -1 & & f[z_4,z_3,z_2,z_1] = -6 & & -10 & & & \\
z_3 = 0 & f[z_3] = 1 & & f[z_4,z_3,z_2] = 1 & & 5 & & 4 & & \\
& & \frac{f'(z_3)}{1} = 0 & & f[z_5,z_4,z_3,z_2] = -1 & & -2 & & -1 & \\
z_4 = 0 & f[z_4] = 1 & & \frac{f''(z_4)}{2} = 0 & & 1 & & 2 & & 1 \\
& & \frac{f'(z_4)}{1} = 0 & & f[z_6,z_5,z_4,z_3] = 1 & & 2 & & 1 & \\
z_5 = 0 & f[z_5] = 1 & & f[z_6,z_5,z_4] = 1 & & 5 & & 4 & & \\
& & f[z_6,z_5] = 1 & & f[z_7,z_6,z_5,z_4] = 6 & & 10 & & & \\
z_6 = 1 & f[z_6] = 2 & & f[z_7,z_6,z_5] = 7 & & 15 & & & & \\
& & \frac{f'(z_7)}{1} = 8 & & f[z_8,z_7,z_6,z_5] = 21 & & & & & \\
z_7 = 1 & f[z_7] = 2 & & \frac{f''(z_7)}{2} = 28 & & & & & & \\
& & \frac{f'(z_8)}{1} = 8 & & & & & & & \\
z_8 = 1 & f[z_8] = 2 & & & & & & & & \\
\end{matrix}](https://upload.wikimedia.org/math/2/f/2/2f2e3f1ecd6d6ccbf9bd0ae7cac01576.png)
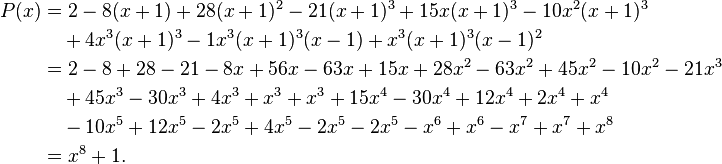
No hay comentarios:
Publicar un comentario