Polinomio irreducible
En teoría de Anillos, un polinomio  no constante (y por lo tanto no nulo) con coeficientes en un dominio íntegro
no constante (y por lo tanto no nulo) con coeficientes en un dominio íntegro  (es decir,
(es decir, ![p \in R[x]](https://upload.wikimedia.org/math/5/5/2/552a3eaa6c85a80febade32555d3e4f4.png) ) es irreducible si no puede factorizarse como producto de polinomios de manera que todos ellos tengan grados menor que
) es irreducible si no puede factorizarse como producto de polinomios de manera que todos ellos tengan grados menor que  . Es decir, si
. Es decir, si  entonces ha de ser
entonces ha de ser 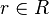 o
o  (es decir, alguno de ellos ha de ser un polinomio constante).
(es decir, alguno de ellos ha de ser un polinomio constante).
 no constante (y por lo tanto no nulo) con coeficientes en un dominio íntegro
no constante (y por lo tanto no nulo) con coeficientes en un dominio íntegro  (es decir,
(es decir, ![p \in R[x]](https://upload.wikimedia.org/math/5/5/2/552a3eaa6c85a80febade32555d3e4f4.png) ) es irreducible si no puede factorizarse como producto de polinomios de manera que todos ellos tengan grados menor que
) es irreducible si no puede factorizarse como producto de polinomios de manera que todos ellos tengan grados menor que  . Es decir, si
. Es decir, si  entonces ha de ser
entonces ha de ser 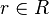 o
o  (es decir, alguno de ellos ha de ser un polinomio constante).
(es decir, alguno de ellos ha de ser un polinomio constante).
Esto es un caso particular de elemento irreducible en un dominio íntegro.
El dominio íntegro R puede, entre otros, ser el conjunto 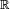 de los números reales (que es dominio íntegro por ser cuerpo), el conjunto
de los números reales (que es dominio íntegro por ser cuerpo), el conjunto 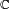 de los números complejos (también cuerpo), el conjunto
de los números complejos (también cuerpo), el conjunto  de los números racionales (cuerpo también) o el conjunto
de los números racionales (cuerpo también) o el conjunto  de los números enteros (que no es cuerpo pero sí dominio íntegro).
de los números enteros (que no es cuerpo pero sí dominio íntegro).
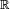 de los números reales (que es dominio íntegro por ser cuerpo), el conjunto
de los números reales (que es dominio íntegro por ser cuerpo), el conjunto 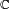 de los números complejos (también cuerpo), el conjunto
de los números complejos (también cuerpo), el conjunto  de los números racionales (cuerpo también) o el conjunto
de los números racionales (cuerpo también) o el conjunto  de los números enteros (que no es cuerpo pero sí dominio íntegro).
de los números enteros (que no es cuerpo pero sí dominio íntegro).Ejemplos
Los cinco polinomios siguientes demuestran algunas características elementales de los polinomios reducibles e irreducibles, dependiendo del dominio de integridaddonde estén definidos:
 ,
, ,
, ,
, ,
, .
.
- Sobre el anillo
 de números enteros, los primeros dos polinomios son reducibles, pero los tres últimos son irreducibles (el tercero no tiene coeficientes del número entero).
de números enteros, los primeros dos polinomios son reducibles, pero los tres últimos son irreducibles (el tercero no tiene coeficientes del número entero). - Sobre el cuerpo
 de números racionales, los primeros tres polinomios son reducibles, pero los otros dos son irreducibles.
de números racionales, los primeros tres polinomios son reducibles, pero los otros dos son irreducibles. - Sobre el cuerpo
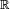 de números reales, los primeros cuatro polinomios son reducibles, pero el quinto sigue siendo irreducible.
de números reales, los primeros cuatro polinomios son reducibles, pero el quinto sigue siendo irreducible. - Sobre el cuerpo
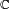 de números complejos, los cinco polinomios son reducibles. De hecho en
de números complejos, los cinco polinomios son reducibles. De hecho en 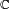 , cada polinomio no-constante se puede descomponer en factores lineales
, cada polinomio no-constante se puede descomponer en factores lineales

- donde
 es el coeficiente principal del polinomio y
es el coeficiente principal del polinomio y 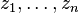 son los ceros de
son los ceros de 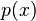 . Por lo tanto, todos los polinomios irreducibles son de grado 1.
. Por lo tanto, todos los polinomios irreducibles son de grado 1.
En el caso del cuerpo 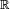 , tampoco pueden ser reducibles aquellos polinomios de grado 2 con discriminante negativo, ya que a pesar de ser factorizado por polinomios de menor grado que éste, y mayor o igual a 0, no tienen sus coeficientes dentro del cuerpo de los reales. Éste es el teorema fundamental del álgebra.
, tampoco pueden ser reducibles aquellos polinomios de grado 2 con discriminante negativo, ya que a pesar de ser factorizado por polinomios de menor grado que éste, y mayor o igual a 0, no tienen sus coeficientes dentro del cuerpo de los reales. Éste es el teorema fundamental del álgebra.
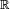 , tampoco pueden ser reducibles aquellos polinomios de grado 2 con discriminante negativo, ya que a pesar de ser factorizado por polinomios de menor grado que éste, y mayor o igual a 0, no tienen sus coeficientes dentro del cuerpo de los reales. Éste es el teorema fundamental del álgebra.
, tampoco pueden ser reducibles aquellos polinomios de grado 2 con discriminante negativo, ya que a pesar de ser factorizado por polinomios de menor grado que éste, y mayor o igual a 0, no tienen sus coeficientes dentro del cuerpo de los reales. Éste es el teorema fundamental del álgebra.Criterios de irreducibilidad
Para demostrar si un polinomio es irreducible se pueden aplicar varios criterios, entre los que se encuentran el criterio de Eisenstein, el criterio de reducción o el Lema de Gauss. Aparte, todos los polinomios primitivos son irreducibles, aunque el recíproco no es cierto. Un polinomio irreducible es polinomio primitivo si y solo si  cuando p es primo y x es un elemento de orden
cuando p es primo y x es un elemento de orden ![p^m \in \mathbb{Z}_p[x]/f(x)](https://upload.wikimedia.org/math/6/d/a/6da5fbe6727f6d494fe2f7bd2400612c.png) .
.
 cuando p es primo y x es un elemento de orden
cuando p es primo y x es un elemento de orden ![p^m \in \mathbb{Z}_p[x]/f(x)](https://upload.wikimedia.org/math/6/d/a/6da5fbe6727f6d494fe2f7bd2400612c.png) .
.Polinomios irreducibles de Z[x]
- Un polinomio
 es irreducible sobre
es irreducible sobre ![\scriptstyle \mathbb{Z}[X]](https://upload.wikimedia.org/math/3/6/a/36a0288d875d693cbd5dd2047e656ac2.png) , si y sólo si
, si y sólo si  también es irreducible.
también es irreducible. - Trivialmente un polinomio de segundo grado, que no tenga a 1 o -1 como raíz, sólo puede ser reducible si su término independiente no es un número primo:
 , si
, si  , entonces la reducibilidad implica que el término independiente tiene dos divisores no triviales y por tanto no puede ser primo.
, entonces la reducibilidad implica que el término independiente tiene dos divisores no triviales y por tanto no puede ser primo.
Polinomios irreducibles de Q[x]
Lema de Gauss: Si un polinomio  es irreducible sobre
es irreducible sobre ![\scriptstyle \mathbb{Z}[X]](https://upload.wikimedia.org/math/3/6/a/36a0288d875d693cbd5dd2047e656ac2.png) , entonces también es irreducible considerado sobre
, entonces también es irreducible considerado sobre ![\scriptstyle \mathbb{Q}[X]](https://upload.wikimedia.org/math/4/7/1/471d9c949d23a992c278bf405ca8a616.png) .1
.1
 es irreducible sobre
es irreducible sobre ![\scriptstyle \mathbb{Z}[X]](https://upload.wikimedia.org/math/3/6/a/36a0288d875d693cbd5dd2047e656ac2.png) , entonces también es irreducible considerado sobre
, entonces también es irreducible considerado sobre ![\scriptstyle \mathbb{Q}[X]](https://upload.wikimedia.org/math/4/7/1/471d9c949d23a992c278bf405ca8a616.png) .1
.1Polinomios irreducibles de R[x]
Los polinomios irreducibles sobre ![\scriptstyle \mathbb{R}[X]](https://upload.wikimedia.org/math/b/c/4/bc4df3d185fdccd20a09d5135b0916c2.png) son los monomios y los polinomios
son los monomios y los polinomios  de grado 2, tales que su discriminante sea negativo, es decir:
de grado 2, tales que su discriminante sea negativo, es decir:
![\scriptstyle \mathbb{R}[X]](https://upload.wikimedia.org/math/b/c/4/bc4df3d185fdccd20a09d5135b0916c2.png) son los monomios y los polinomios
son los monomios y los polinomios  de grado 2, tales que su discriminante sea negativo, es decir:
de grado 2, tales que su discriminante sea negativo, es decir:Polinomios irreducibles (primos)
Un polinomio con coeficientes enteros que no pueden ser factorizados en polinomios de grado menor, también con coeficientes enteros, es llamado un polinomio irreducible o primo.
Ejemplo 1:
x2 + x + 1
es un polinomio irreducible. No hay forma de encontrar dos enteros b y c tal que su producto sea 1 y su suma también sea 1, así que no podemos factorizarlo en términos lineales (x +b)(x + c).
Ejemplo 2:
El polinomio
x2 – 2
es irreducible con enteros. Sin embargo, podría factorizarlo como
Los polinomios de Bernstein o polinomios en la base de Bernstein son una clase particular de polinomios en el campo de los números reales, que son utilizados dentro del ámbito del análisis numérico. El nombre hace referencia al matemático ucraniano Sergei Natanovich Bernstein.
El algoritmo de evaluación más numéricamente estable es el de De Casteljau.Definición
Un polinomio de Bernstein  de orden n aproxima una función
de orden n aproxima una función 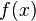 en un intervalo, mejor cuanto mayor sea n, a partir de esta fórmula:
en un intervalo, mejor cuanto mayor sea n, a partir de esta fórmula:
 de orden n aproxima una función
de orden n aproxima una función 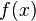 en un intervalo, mejor cuanto mayor sea n, a partir de esta fórmula:
en un intervalo, mejor cuanto mayor sea n, a partir de esta fórmula:
donde los  son elementos de la distribución binomial respecto de la variable
son elementos de la distribución binomial respecto de la variable  y los
y los  son valores de la función que queremos aproximar.
son valores de la función que queremos aproximar.
 son elementos de la distribución binomial respecto de la variable
son elementos de la distribución binomial respecto de la variable  y los
y los  son valores de la función que queremos aproximar.
son valores de la función que queremos aproximar.
Para aproximar la función en el intervalo ![[0,1] \,](https://upload.wikimedia.org/math/d/0/9/d09694b77d8a3a03f6879fa37f09d0b0.png) estos elementos toman los siguientes valores:
estos elementos toman los siguientes valores:
![[0,1] \,](https://upload.wikimedia.org/math/d/0/9/d09694b77d8a3a03f6879fa37f09d0b0.png) estos elementos toman los siguientes valores:
estos elementos toman los siguientes valores:
(aquí  es el coeficiente binomial).
es el coeficiente binomial).
 es el coeficiente binomial).
es el coeficiente binomial).
y más en general transformando las ecuaciones para un intervalo ![[a,b] \,](https://upload.wikimedia.org/math/7/f/3/7f3408c72246eece3d5542fc853ce417.png) , los
, los ![B^n_{i}(x)_{[a,b]}](https://upload.wikimedia.org/math/6/5/b/65b86b08120f1600ca679847678016b8.png) se convierten en polinomios de la base de Bernstein:
se convierten en polinomios de la base de Bernstein:
![[a,b] \,](https://upload.wikimedia.org/math/7/f/3/7f3408c72246eece3d5542fc853ce417.png) , los
, los ![B^n_{i}(x)_{[a,b]}](https://upload.wikimedia.org/math/6/5/b/65b86b08120f1600ca679847678016b8.png) se convierten en polinomios de la base de Bernstein:
se convierten en polinomios de la base de Bernstein:
Así, la fórmula general desarrollada es:
Propiedades
Para un grado n, existen n+1 polinomios de Bernstein  definidos sobre el intervalo
definidos sobre el intervalo ![[a,b] \,](https://upload.wikimedia.org/math/7/f/3/7f3408c72246eece3d5542fc853ce417.png) , por
, por
 definidos sobre el intervalo
definidos sobre el intervalo ![[a,b] \,](https://upload.wikimedia.org/math/7/f/3/7f3408c72246eece3d5542fc853ce417.png) , por
, por
Estos polinomios presentan estas propiedades importantes, que cumplen para cualquier valor de  en el intervalo
en el intervalo ![[a,b] \,](https://upload.wikimedia.org/math/7/f/3/7f3408c72246eece3d5542fc853ce417.png)
 en el intervalo
en el intervalo ![[a,b] \,](https://upload.wikimedia.org/math/7/f/3/7f3408c72246eece3d5542fc853ce417.png)
- Partición de la unidad :

- Positividad :

- Simetría :

Las dos primeras propiedades nos indican que forman una combinación convexa. La modificación por escala y traslación de intervalo no influye sobre los coeficientes del polinomio en cuestión. Se ha de notar la gran semejanza de estos polinomios con la distribución binomial.
Para el intervalo ![[0,1] \,](https://upload.wikimedia.org/math/d/0/9/d09694b77d8a3a03f6879fa37f09d0b0.png) existe esta fórmula de recurrencia:
existe esta fórmula de recurrencia:
![[0,1] \,](https://upload.wikimedia.org/math/d/0/9/d09694b77d8a3a03f6879fa37f09d0b0.png) existe esta fórmula de recurrencia:
existe esta fórmula de recurrencia: .
.
Ejemplo
En el caso de un polinomio de orden  la base en
la base en ![[0,1] \,](https://upload.wikimedia.org/math/d/0/9/d09694b77d8a3a03f6879fa37f09d0b0.png) está compuesta de:
está compuesta de:
 la base en
la base en ![[0,1] \,](https://upload.wikimedia.org/math/d/0/9/d09694b77d8a3a03f6879fa37f09d0b0.png) está compuesta de:
está compuesta de:
Un polinomio expresado en esta base tendría entonces la forma:
Si aproximamos  obtenemos el mismo polinomio:
obtenemos el mismo polinomio: 
 obtenemos el mismo polinomio:
obtenemos el mismo polinomio: 
si evaluamos  aproxima a:
aproxima a: 
 aproxima a:
aproxima a: 
y probando con  resulta:
resulta: 
 resulta:
resulta: 
Aplicaciones
Los polinomios de Bernstein son utilizados para demostrar el teorema de aproximación de Weierstrass y por esto son también utilizados para efectuar aproximaciones e interpolaciones de funciones como, por ejemplo, la curva de Beziér, así como para la estimación de las funciones de densidad de probabilidad:
Para n que tiende al infinito, el polinomio converge uniformamente hacia la función f (x), o sea
donde
 , llamado módulo de continuidad.
, llamado módulo de continuidad.Introducción
Como introducción del trabajo que desarrollaremos posteriormente, recordemos la definición de polinomios de Bernstein en su forma usual.Definición [Polinomios de Bernstein]Sea![f : [0, 1] --> ÷µ](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_1.gif) una función continua. El polinomio n-ésimo de Bernstein
una función continua. El polinomio n-ésimo de Bernstein  de la función
de la función  se define como:
se define como:![B(n, f, x) = B _ n(f, x) = Underoverscript[∑, k = 0, arg3] f(k/n) ( n ) x^k(1 - x)^(n - k), k](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_4.gif) donde
donde .Una construción de los polinomios de Bernstein para la función constante
.Una construción de los polinomios de Bernstein para la función constante sobre el intervalo
sobre el intervalo ![[0, 1]](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_7.gif) , la hacemos de la siguiente formaObservemos que
, la hacemos de la siguiente formaObservemos que ,
,  . Por lo tanto,
. Por lo tanto,  se cumple que:
se cumple que:![1 = (x + 1 - x)^n = Underoverscript[∑, k = 0, arg3] ( n ) x^k (1 - x)^(n - k) k](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_11.gif) lo cual nos dice que el n-ésimo polinomio de Berntein de la función constante
lo cual nos dice que el n-ésimo polinomio de Berntein de la función constante coincide con
coincide con  , o sea es 1.Con esto como preámbulo y asumiendo que
, o sea es 1.Con esto como preámbulo y asumiendo que![f : [0, 1] --> ÷µ](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_14.gif) es continua, definimos en Mathematica el n-ésimo polinomio de Bernstein evaluado en
es continua, definimos en Mathematica el n-ésimo polinomio de Bernstein evaluado en  de la siguiente forma:In[1]:=
de la siguiente forma:In[1]:=![B[n_, f_, x_] := Underoverscript[∑, k = 0, arg3] Binomial[n, k] x^k (1 - x)^(n - k) f[k/n] ;](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_16.gif) No deja de ser interesante que Mathematica acepta ese procedimento sin dificultad, logrando resultados como los siguiente:In[2]:=
No deja de ser interesante que Mathematica acepta ese procedimento sin dificultad, logrando resultados como los siguiente:In[2]:=![B[n, f, x] /. f -> (# &)](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_17.gif) Out[2]=
Out[2]= Observemos que Mathematica no simplifica el resultado. Para lograr una expresión más simple debemos definir la siguiente regla lógica:In[3]:=
Observemos que Mathematica no simplifica el resultado. Para lograr una expresión más simple debemos definir la siguiente regla lógica:In[3]:=![regla = {(1 - x)^n (-1/(-1 + x))^n -> 1, (1 - x)^n (1/(1 - x))^n -> 1} ; B[n, f, x] /. f -> (# &) /. regla](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_19.gif) Out[4]=
Out[4]= Es decir, el polinomio n-ésimo de Bernstein de la función
Es decir, el polinomio n-ésimo de Bernstein de la función coincide con
coincide con  , o sea es
, o sea es  .Veamos otros ejemplos en los cuales la función
.Veamos otros ejemplos en los cuales la función esta definida por
esta definida por  ,
,  ,
,  ,
,  , Sen(x) + 3
, Sen(x) + 3 , respectivamente.Para la función
, respectivamente.Para la función In[5]:=
In[5]:=![Apart[Simplify[Expand[B[n, f, x] /. f -> (#^2 &)]] /. regla, x]](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_31.gif) Out[5]=
Out[5]= obtenemos que el n-ésimo polinomio de Bernstein es:
obtenemos que el n-ésimo polinomio de Bernstein es: Para la función
Para la función In[6]:=
In[6]:=![Apart[ Simplify[Expand[B[n, f, x] /. f -> (#^3 &)]] /. regla]](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_35.gif) Out[6]=
Out[6]= obtenemos que el n-ésimo polinomio de Bernstein es:
obtenemos que el n-ésimo polinomio de Bernstein es: Para la función
Para la función In[7]:=
In[7]:=![Apart[Simplify[Expand[B[n, f, x] /. f -> (#^4 &)]] /. regla, x]](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_39.gif) Out[7]=
Out[7]=
 obtenemos que el n-ésimo polinomio de Bernstein es:
obtenemos que el n-ésimo polinomio de Bernstein es: Para la función
Para la función obtenemos queIn[8]:=
obtenemos queIn[8]:=![Apart[Simplify[Expand[B[n, f, x] /. f -> (3 * #^4 + #^2 &)]] /. regla, x]](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_44.gif) Out[8]=
Out[8]= y para la función
y para la función obtenemos queIn[9]:=
obtenemos queIn[9]:=![Apart[Simplify[Expand[B[n, f, x] /. f -> (Sin[#] + 3 * #^4 + #^2 &)]] /. regla, x]](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_47.gif) Out[9]=
Out[9]= Observe el uso que se dió a la función pura (#&), si no se usan los paréntesis el procedimiento no funciona.Los polinomios de Bernstein tiene las siguientes propiedades:• Si
Observe el uso que se dió a la función pura (#&), si no se usan los paréntesis el procedimiento no funciona.Los polinomios de Bernstein tiene las siguientes propiedades:• Si![f : [0, 1] --> ÷µ](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_49.gif) es continua entonces
es continua entonces ![B[n, f, x] = B _ n[f, x]](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_50.gif) es una función continua.• Si
es una función continua.• Si entonces
entonces ![B[n, f, x] = B _ n[f, x] >= 0](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_52.gif) , para toda
, para toda  .Además, en
.Además, en![÷r ( [0, 1], {| {| _ 8)](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_54.gif) se cumple que para toda
se cumple que para toda ![f ∈ ÷r([0, 1])](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_55.gif) se tiene que
se tiene que ![B[n, f, x] --> f](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_56.gif) con la norma
con la norma  . Es decir, la convergencia es uniforme. La demostración se basa en los siguientes hechos:Primero, como
. Es decir, la convergencia es uniforme. La demostración se basa en los siguientes hechos:Primero, como es continua en
es continua en ![[0, 1]](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_59.gif) entonces
entonces  es acotada y podemos elegir
es acotada y podemos elegir ![M = Underscript[Sup, 0 <= x <= 1] {f(x)}](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_61.gif) , con lo cual
, con lo cual ,
, ![∀ x ∈ [0, 1]](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_63.gif) Por otro lado, al ser
Por otro lado, al ser continua en
continua en ![[0, 1]](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_65.gif) , para cualquier
, para cualquier  existe un
existe un  tal que para todo
tal que para todo  ,
, ![y ∈ [0, 1]](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_69.gif) , que cumplen
, que cumplen  se tine que
se tine que  Con las definiciones anteriores de
Con las definiciones anteriores de ,
,  ,
,  , podemos afirmar que:
, podemos afirmar que:![-ζ - 2 M/δ^2 (x - y)^2 <= f (x) - f (y) <= ζ + 2 M/δ^2 (x - y)^2, ∀ x, y ∈ [0, 1]](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_75.gif) Con esto, el resto de la demostración es sencilla. Esencialmente ésta es la demostración del teorema de Korovkin. (El Lic. Gerardo Araya escribió una excelente tesis de graduación sobre este tema, dirigida por el profesor Vernor Arguedas [1])Es importante recalcar que los polinomios de Bernstein aproximan a la función
Con esto, el resto de la demostración es sencilla. Esencialmente ésta es la demostración del teorema de Korovkin. (El Lic. Gerardo Araya escribió una excelente tesis de graduación sobre este tema, dirigida por el profesor Vernor Arguedas [1])Es importante recalcar que los polinomios de Bernstein aproximan a la función , no la interpolan necesariamente.
, no la interpolan necesariamente. Los términos intermedios en la construcción del n-ésimo polinomio de Bernstein de la función
Los términos intermedios en la construcción del n-ésimo polinomio de Bernstein de la función :
:
 son muy útiles.Usando Mathematica podemos graficar los términos intermedios del polinomio de Bernstein
son muy útiles.Usando Mathematica podemos graficar los términos intermedios del polinomio de Bernstein (observe que
(observe que  ):In[60]:=
):In[60]:=![Bernstein2[i_, n_] := Binomial[n, i] x^i (1 - x)^(n - i) ; Bernstein2[n_] := Table[Bernstein2 ... gt; {AbsolutePointSize[5], Table[Point[{i/n, Bernstein2[i, n] /. x -> i/n}], {i, 0, n} ] }]] ;](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_83.gif)
 Out[63]=
Out[63]=

![[Graphics:HTMLFiles/index_87.gif]](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_87.gif) Figura 1: Gráfica de los términos intermedios del 4-ésimo polinomio de Bernstein.In[67]:=
Figura 1: Gráfica de los términos intermedios del 4-ésimo polinomio de Bernstein.In[67]:=![Plot[Evaluate[Bernstein2 [n], {x, 0, 1}, PlotStyle -> { {RGBColor[0, 0, 1], Thickness[0.007 ... , 0, 1], Thickness[0.007], Line[Table[{i/n, Bernstein2[i, n] /. x -> i/n}, {i, 0, n} ] ]}}]] ;](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_88.gif)
![[Graphics:HTMLFiles/index_89.gif]](https://tecdigital.tec.ac.cr/revistamatematica/ContribucionesV5n1Jun2004/MataArguedas/imagenes/index_89.gif) Figura 2: Términos intermedios de 4-ésimo polinomio de Bernstein.
Figura 2: Términos intermedios de 4-ésimo polinomio de Bernstein.



![c_i = f \left( i \, \frac{b-a}{n}+a \right) \qquad \text{y} \qquad B^n_i (x)_{[a,b]} = {n \choose i} {(x-a)^i (b-x)^{n-i} \over (b-a)^n}](https://upload.wikimedia.org/math/e/b/3/eb38a889b79cb75ba75a3e069502aabb.png)


![B^n_i (x) _{[a,b]} = {n \choose i} {(x-a)^i (b-x)^{n-i} \over (b-a)^n}](https://upload.wikimedia.org/math/e/2/2/e22b11d00b1f0940a51a25ff3ef4108e.png)





No hay comentarios:
Publicar un comentario