AMIGOS PARA SIEMPRE: Polinomios

función cuadrática de una variable es una función polinómica definida por:

$y = ax^2 + bx + c \,$

con

a \ne 0

.¹ También se da el caso que se le llame Trinomio cuadrático² . También se denomina función cuadrática a funciones definidas por polinomios cuadráticos de más de una variable, como por ejemplo:

$f(x,y) = Ax^2+Bxy+Cy^2+Dx+Ey+F$

En este caso el conjunto de puntos que resultan al igualar el polinomio a cero representan lugares geométricos que siempre es posible reducir a una de las formas:

$\left( \frac{x}{a} \right)^2 \pm \left( \frac{y}{b} \right)^2 = c^2, \qquad \left( \frac{x}{a} \right)^2 \pm \frac{y}{b} = c$

Que corresponden a tres tipos de secciones cónicas (elipse, hipérbola y parábola).

Función cuadrática
Gráfica de Función cuadrática
Definición	$f(x) = ax^2 + bx + c \,$
Tipo	Curva parabólica
Dominio	$\mathbb{R}$
Imagen	$[\frac{4ac-b^2}{4a},+\infty) \text{o} (-\infty ,\frac{4ac-b^2}{4a} ]$
Cálculo infinitesimal
Derivada	$f'(x) = 2ax + b \,$
Límites	ninguno

Funciones cuadráticas de una variable

Las gráficas de estas funciones corresponden a parábolas verticales (eje de simetría paralelo al eje de las ordenadas), con la particularidad de que cuando a>0, el vérticede la parábola se encuentra en la parte inferior de la misma, siendo un mínimo (es decir, la parábola se abre "hacia arriba"), y cuando a<0 abajo="" abre="" bola="" decir="" el="" en="" encuentra="" es="" hacia="" la="" m="" p="" par="" parte="" rtice="" se="" siendo="" superior="" un="" v="" ximo="">

El estudio de las funciones cuadráticas tiene numerosas aplicaciones en campos muy diversos, como por ejemplo la caída libre o el tiro parabólico.

La función derivada de una función cuadrática es una función lineal y su integral indefinida es una familia de funciones cúbicas.

Raíces

Véase también: Ecuación de segundo grado

Las raíces (o ceros) de una función cuadrática, como en toda función, son los valores de x, para los cuales

a x^2 + bx + c = 0 \

. Son denotadas habitualmente como:

x_1

x_2

, dependiendo del valor del discriminante Δ definido como $\Delta = b^2 - 4 a c \$ .

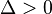Dos soluciones reales y diferentes si el discriminante es positivo, $\Delta > 0$ :

x_1 = \frac{-b + \sqrt {\Delta}}{2a}

x_2 = \frac{-b - \sqrt {\Delta}}{2a}

Corta la parábola al eje X en dos puntos diferentes.

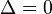Una solución real(o solución doble) si el discriminante es cero, $\Delta = 0$ :

x_1 = x_2 = -\frac{b}{2a}

La parábola es tangente al eje X.

La parábola no corta al eje X.

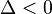El único caso restante es que el discriminante sea negativo, $\Delta < 0$ .

En tal caso, las raíces no son reales, sino que son dos números complejos conjugados:

x_1 = \frac{-b}{2a} + i \frac{\sqrt {-\Delta}}{2a}

x_2 = \frac{-b}{2a} - i \frac{\sqrt {-\Delta}}{2a}

Representación analítica

Hay tres formas de escribir una función cuadrática, aplicables según el uso que se le quiera dar a la función, un estudio analítico de la función o de la ecuación cuadrática, una interpretación o construcción geométrica de la parábola, etc.

Forma desarrollada o polinómica

La forma desarrollada de una función cuadrática (o forma estándar) corresponde a la del polinomio de segundo grado, escrito convencionalmente como:

f(x) = ax^2 + bx + c \,

con

a \neq 0

Forma factorizada

Toda función cuadrática se puede escribir en forma factorizada en función de sus raíces como:

f(x) = a(x - x_1)(x - x_2) \,

siendo a el coeficiente principal de la función, y

x_1

x_2

las raíces de

f(x)

. En el caso de que el discriminante Δ sea igual a 0 entonces

x_1 = x_2

por lo que la factorización adquiere la forma:

f(x) = a(x - x_1)^2 \,

En este caso a

x_1

se la denomina raíz doble, ya que su orden de multiplicidad es 2. Si el discriminante es negativo, las soluciones son complejas, no cabe la factorización.³

Forma canónica

Toda función cuadrática puede ser expresada mediante el cuadrado de un binomio de la siguiente manera:

$f(x) = a (x - h)^2 + k \,$

siendo a el coeficiente principal y el par ordenado (h, k) las coordenadas del vértice de la parábola.

Representación gráfica

Intersección con el eje y

La función corta el eje y en el punto y = f(0), es decir, la parábola corta el eje y cuando x vale cero (0):

$y = f(0) = a \cdot 0^2 + b \cdot 0 + c \,$

lo que resulta:

$y = f(0) = c \,$

la función corta el eje y en el punto (0, c), siendo c el término independiente de la función.

A este punto de la función también se lo conoce con Ordenada al Origen, ya que se da en los términos.

Intersección con el eje x

La función corta al eje x cuando y vale 0, dada la función

y = ax^2 + bx + c \,

es decir:

y = 0 \quad \longmapsto \quad ax^2 + bx + c = 0 \,

las distintas soluciones de esta ecuación de segundo grado, son los casos de corte con el eje x, que se obtienen, como es sabido, por la expresión:

x = \frac{-b \pm \sqrt{b^2 - 4 a c}}{2 a}

Si la función no corta al eje x, las raíces de la función cuadrática son dobles, es decir,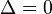

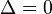\Delta = 0

. Gráficamente la curva de la función (parábola) es tangente al eje de las abscisas. Puede ocurrir que no tenga intersecciones con el eje x, un ejemplo de esto

y=x^2+2

Extremo

En principio, en matemáticas se nombra como extremo tanto al máximo como al mínimo, por ejemplo en el conjunto S = {1,5,9, 13, 17} el mínimo es 1 y el máximo17, y los extremos son 1 y 17. Para calcular el extremo de un trinomio cuadrático, se puede usar un teorema, abordable en álgebra elemental, apoyándose en el comportamiento de una suma de un cuadrado de una variable con un número real cualquiera.⁴

Teorema fundamental del trinomio cuadrático

El trinomio cuadrático real

$y = ax^2+bx+c$ ̝

tiene un valor extremo que lo consigue cuando

$x = \frac{-b}{2a}$

este valor resulta mínimo si a > 0, máximo si a < 0. Si existe y_máx, no existe y_mín , y recíprocamente.⁵ Se abreviará como TFTC.

Problema 1

Descomponer el número positivo s, en dos sumandos, de tal modo que el producto de ellos sea máximo. Sea uno de los sumando x , el otro sumando será s-x y su producto p = x(s-x)

p = -x² + sx.

Luego aplicando el TFTC resulta x = s/2; en tal caso s-x = s/2. En consecuencia el producto alcanza el valor máximo si ambos sumandos son iguales. Si la suma es 30 el producto se alcanza cuando los sumados son 15 y 15, cuyo producto es 225.⁶

Problema 2

Se tiene una alambrada de 120 metros para cerca un terreno rectangular, hallar la máxima área de terreno a cercar. Si los lados miden x, y se tiene que 2x + 2y = 100 de donde y = 50-x y el área es

A = x(50-x) = -x²+5ox y aplicando el TFTC y el resultado anterior, puesto que la suma x + (50-x) = 50 el producto A es máximo cuando x = 50-x, o bien x= 25.

Luego la máxima área es

25\times 25 = 625

Alternativa del cálculo diferencial

Toda función cuadrática posee un máximo o un mínimo, que es el vértice de la parábola. Si la parábola tiene concavidad hacia arriba, el vértice corresponde a un mínimo de la función; mientras que si la parábola tiene concavidad hacia abajo, el vértice será un máximo.

Dada la función en su forma desarrollada:

f(x) = ax^2+bx+c\,

, la coordenada x del vértice será simplemente:

x = \frac{-b}{2a}

. La coordenada y del vértice corresponde a la función f evaluada en ese punto.

Dada la forma canónica:

f(x)=a (x-h)^2+k \,

, las coordenadas explícitas del vértice son: (h,k)

la derivada de la función, y se iguala a cero, la solución a esta ecuación son los posibles máximos y mínimos de la función, en este caso, partiendo de la función cuadrática:

y = ax^2 + bx + c \,

calculamos su derivada respecto a x:

\frac{dy}{dx} ax^2 + bx + c = 2ax + b

que si la igualamos a cero, tenemos:

2ax + b = 0 \,

donde x valdrá:

Para saber si es un máximo o un mínimo es necesario ver la derivada segunda de la función, veamos:

\frac{d^2y}{dx^2} \; ax^2 + bx + c = \frac{dy}{dx} \; 2ax + b = 2a

esto es: 2a será positivo cuando a sea positivo y negativo si a es negativo, por tanto, si la derivada segunda 2a es positiva la parábola es cóncava y el punto será un mínimo de la función, si a es negativa la parábola será convexa y sea un máximo.

Ejemplo 1

Dada la función:

y = (x^2).3 - x - 23 \,

Observación : Es indiferente notar "y" o notar "f(x)". Ambas expresiones hacen referencia a la imagen de x obtenida a través de la función trabajada.

Calculamos su derivada primera:

\frac{dy}{dx} \; (x^2).3 - x - 23 = 6x - 1

Esta derivada valdrá cero:

\frac{dy}{dx} = 0

cuando:

6x - 1 = 0 \,

esto es:

6x = 1 \,

x = \cfrac{1}{6}

Esta función presenta un extremo relativo para

x = \frac{1}{6}

, veamos si es un máximo o un mínimo, calculando la derivada segunda:

\frac{d^2y}{dx^2} \; (x^2).3 - x - 23 = \frac{dy}{dx} \; 6x - 1 = 6

Que es 6, dado que 6 es un valor positivo, la función es cóncava, y el extremo relativo que presente para:

x = \cfrac{1}{6}

, es un mínimo.

Obs. Observando el signo de la constante "a" podemos saber de antemano si estamos ante un mínimo o un máximo. Entonces para a<0 a="" m="" para="" tendremos="" un="" ximo="" y="">0 un mínimo.

Ejemplo 2

Dada la función:

y = -x^2 + 4x + 5 \,

Para calcular sus extremos relativos calcularemos su derivada primera:

\frac{d}{dx} \;( -x^2 + 4x + 5 )= -2x + 4

Esta derivada valdrá cero cuando:

-2x + 4 = 0 \,

esto es:

2x = 4 \,

que resulta:

x = 2 \,

Para

x = 2

, la función presenta un extremo relativo, como sabemos que el coeficiente de

x^2

, es negativo es un máximo. Si realizamos el estudio de signo de la derivada primera, nos da que en

x = 2

pasa de ser positivo a negativo, o sea la función cambia de ser creciente a decreciente, por lo que confirmamos que es un máximo. De otra forma; se puede calcular la derivada segunda en este punto, comprobando si la función es cóncava o convexa.

Otros procedimientos

Si es posible factorizar en la forma $y = a(x - x_1)(x - x_2) \,$ , se halla el máximo del producto de los dos factores binómicos, teniendo en cuenta que

tal caso ocurre si los factores son iguales, luego haciendo

x -x_1 = x - x_ 2 \,

se obtiene

x = (x_1 + x_2)/ 2 \,

o bien

x = -b/2a \,

.⁷ El signo de a determina si es mínimo o máximo.

La forma canónica se puede escribir como $1/af(x) = (x - h)^2 + k/a \,$ , donde el segundo término conlleva un cuadrado, que es ≥ 0; pero en el segundo miembro si k/a es positivo, hay mínimo con x = h; si k/a es negativo, se obtiene un máximo si x = h.⁸ Todo ello para la función g(x)= 1/af(x).

Presencia

En cinemática

en la ecuación del espacio en caso del movimiento uniforme acelerado:

f(x) = a t^2 + v_0t + e_0 \,

, donde a aceleración,

v_0\,

, velocidad inicial,

e_0 \,

espacio inicial y t, variable del tiempo.,⁹

En geometría

En el área total de un cilindro, como función del radio de la base; de l modo en el área total del cono, en función del radio.

En el área total de un prisma cuadrado, función del lado de la base, altura constante, lo mismo para la pirámide cuadrada.¹⁰

Presencia histórica

Arquímedes calculó el área de un sector parabólico, limitado por un rectángulo, en términos modernos según la función

x= f(y) = y^2 \,

.¹¹

Determinar la ecuación conocidos tres puntos

Partiendo de la forma de la ecuación:

y = ax^2 +bx +c \,

y conocidos tres puntos del plano xy por los que pasa una función polinómica de segundo grado:

(x_1,y_1), \; (x_2,y_2), \; (x_3,y_3)

se cumplirá que:

\left \{ \begin{matrix} y_1 = ax_{1}^2 +bx_1 +c \\ y_2 = ax_{2}^2 +bx_2 +c \\ y_3 = ax_{3}^2 +bx_3 +c \end{matrix} \right .

con lo que tenemos un sistema de tres ecuaciones con tres incógnitas, donde las incógnitas son: a, b y c, este sistema tendrá solución si el determinante de los coeficientes de las incógnitas es distinto de cero.

Representando el sistema ordenado de forma convencional:

\left \{ \begin{matrix} ax_{1}^2 +bx_1 +c = y_1 \\ ax_{2}^2 +bx_2 +c = y_2 \\ ax_{3}^2 +bx_3 +c = y_3 \end{matrix} \right .

Con lo que podemos calcular los valores de los coeficientes:

a = \cfrac{ \left | \begin{matrix} y_1 & x_1 & 1 \\ y_2 & x_2 & 1 \\ y_3 & x_3 & 1 \end{matrix} \right | }{ \left | \begin{matrix} x_{1}^2 & x_1 & 1 \\ x_{2}^2 & x_2 & 1 \\ x_{3}^2 & x_3 & 1 \end{matrix} \right | }

, \quad b = \cfrac{ \left | \begin{matrix} x_{1}^2 & y_1 & 1 \\ x_{2}^2 & y_2 & 1 \\ x_{3}^2 & y_3 & 1 \end{matrix} \right | }{ \left | \begin{matrix} x_{1}^2 & x_1 & 1 \\ x_{2}^2 & x_2 & 1 \\ x_{3}^2 & x_3 & 1 \end{matrix} \right | }

, \quad c = \cfrac{ \left | \begin{matrix} x_{1}^2 & x_1 & y_1 \\ x_{2}^2 & x_2 & y_2 \\ x_{3}^2 & x_3 & y_3 \end{matrix} \right | }{ \left | \begin{matrix} x_{1}^2 & x_1 & 1 \\ x_{2}^2 & x_2 & 1 \\ x_{3}^2 & x_3 & 1 \end{matrix} \right | }

Función cuadrática

Son funciones polinómicas es de segundo grado, siendo su gráfica una parábola.

f(x) = ax² + bx + c

Representación gráfica de la parábola

Podemos construir una parábola a partir de estos puntos:

1. Vértice

Por el vértice pasa el eje de simetría de la parábola.

La ecuación del eje de simetría es:

2. Puntos de corte con el eje OX

En el eje de abscisas la segunda coordenada es cero, por lo que tendremos:

ax² + bx + c = 0

Resolviendo la ecuación podemos obtener:

Dos puntos de corte: (x₁, 0) y (x₂, 0) si b² − 4ac > 0

Un punto de corte: (x₁, 0) si b² − 4ac = 0

Ningún punto de corte si b² − 4ac < 0

3. Punto de corte con el eje OY

En el eje de ordenadas la primera coordenada es cero, por lo que tendremos:

f(0) = a · 0² + b · 0 + c = c (0,c)

Ejemplo

Representar la función f(x) = x² − 4x + 3.

1. Vértice

x_v = − (−4) / 2 = 2 y_v= 2² − 4· 2 + 3 = −1

V(2, −1)

2. Puntos de corte con el eje OX

x² − 4x + 3 = 0

(3, 0) (1, 0)

3. Punto de corte con el eje OY

(0, 3)

AMIGOS PARA SIEMPRE

Páginas

lunes, 22 de febrero de 2016

Polinomios

Funciones cuadráticas de una variable

Raíces

Representación analítica

Representación gráfica

Extremo

Teorema fundamental del trinomio cuadrático

Alternativa del cálculo diferencial

Ejemplo 1

Ejemplo 2

Otros procedimientos

Presencia

Presencia histórica

Determinar la ecuación conocidos tres puntos

Función cuadrática

Representación gráfica de la parábola

1. Vértice

2. Puntos de corte con el eje OX

3. Punto de corte con el eje OY

1. Vértice

2. Puntos de corte con el eje OX

3. Punto de corte con el eje OY

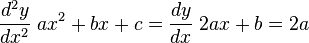
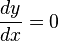
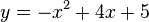
No hay comentarios:

Publicar un comentario

Datos personales

Archivo del blog