AMIGOS PARA SIEMPRE: Matemáticas

martes, 1 de marzo de 2016

Matemáticas - Matrices

matriz bidiagonal es una matriz con elementos distintos de cero tan solo a lo largo de su diagonal principal y de la primera superdiagonal o de la primera subdiagonal. Solo una de estas dos últimas puede estar ocupada.

Por ejemplo, la siguiente matriz es bidiagonal:

\begin{pmatrix} 1 & 4 & 0 & 0 \\ 0 & 4 & 1 & 0 \\ 0 & 0 & 3 & 4 \\ 0 & 0 & 0 & 3 \\ \end{pmatrix}

Cuando la primera superdiagonal está ocupada, la matriz se denomina bidiagonal superior. Cuando la primera subdiagonal está ocupada, la matriz se denomina bidiagonal inferior

\begin{pmatrix} 1 & 0 & 0 & 0 \\ 2 & 4 & 0 & 0 \\ 0 & 3 & 3 & 0 \\ 0 & 0 & 4 & 3 \\ \end{pmatrix}.

La forma general:

T = \begin{pmatrix} a_{1,1} & a_{1,2} & 0 & \dots & 0\\ 0 & a_{2,2} & a_{2,3} & \ddots & \vdots \\ 0 & \ddots & \ddots & \ddots & 0\\ \vdots & \ddots & \ddots & \ddots & a_{n-1,n}\\ 0 & \dots & 0 & 0 & a_{n,n} \end{pmatrix}

Tridiagonales y bidiagonal Matrices

un asimétrico matriz tridiagonal de orden n se almacena en tres matrices unidimensionales, uno de longitud n que contiene los elementos de la diagonal, y dos de longitud n -1 que contiene los elementos subdiagonal y superdiagonal en elementos 1: n -1 .

Un simétrica tridiagonal o bidiagonal matriz se almacena en dos matrices unidimensionales, uno de longitud n que contienen los elementos de la diagonal, y uno de longitud n -1 que contiene los elementos fuera de la diagonal. (Rutinas EISPACK almacenan los elementos fuera de la diagonal de elementos 2: n de un vector de longitud n .)

matriz booleana es una matriz de números cuyas componentes o entradas son exclusivamente ceros o unos. Las matrices booleanas son útiles porque pueden representar objetos abstractos como relaciones binarias o grafos.

Una matriz booleana general de nxm elementos tiene la forma:

$A = \begin{pmatrix} a_{11} & a_{12} & a_{13} & . & . & .& a_{1m}\\ a_{21} & a_{22} & a_{23} & . & . & .& a_{2m}\\ a_{31} & a_{32} & a_{33} & . & . & .& a_{3m}\\ . & . & . & . & . & .& .\\ . & . & . & . & . & .& .\\ . & . & . & . & . & .& .\\ a_{n1} & a_{n2} & a_{n3} & . & . & .& a_{nm}\\ \end{pmatrix}$

Donde a_ij = 0 o a_ij = 1.

Ejemplos

Ejemplos de matrices booleanas son las siguientes:

\begin{bmatrix} 1 & 0 \\ 1 & 0 \\ 0 & 0 \end{bmatrix} \quad \begin{bmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix}

Operaciones con matrices booleanas

Las operaciones que se pueden realizar entre matrices booleanas son tres: unión, conjunción y producto booleano. Sin embargo, estas operaciones no pueden realizarse sobre dos matrices cualesquiera, sino que deben cumplir ciertos criterios para poder llevarse a cabo. En particular, en el caso de la unión y la conjunción, las matrices que intervienen en la operación deben tener el mismo tamaño, y en el caso del producto booleano, las matrices deben cumplir con las mismas condiciones que para formar el producto de matrices.

Unión / Disyunción

Sean A, B y C matrices booleanas de nxm elementos. Se define

A \vee B = C

la unión de A y B, por:

$C[i,j] =\begin{cases} 1, & \mbox{si } A[i,j]= 1\ { o\ } B[i,j]= 1 \\ 0, & \mbox{si }A[i,j]=B[i,j]=0 \end{cases}$

Intersección / Conjunción

Sean A, B y C matrices booleanas de nxm elementos. Se define

A \and B = C

la intersección de A y B, por:

$C[i,j] =\begin{cases} 1, & \mbox{si }A[i,j]=B[i,j]=1 \\ 0, & \mbox{si } A[i,j]= 0\ { o\ } B[i,j]= 0 \end{cases}$

Otras operaciones matriciales

La traspuesta de una matriz booleana es también otra matriz booleana; pero las operaciones con matrices booleanas no siempre producen matrices booleanas. Un ejemplo de operación que no es interna para las matrices booleanas es la suma:

$\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} + \begin{bmatrix} 0 & 1 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 0 & 2 \end{bmatrix}$

Sin embargo, si se consideran las operaciones no sobre números reales sino sobre elementos del cuerpo de característica 2

\scriptstyle \mathbb{Z}_2\ =\ \{\bar{0},\bar{1}\}

queda garantizado que cualquier operación entre matrices booleana es boolena. Para el ejemplo anterior se tiene:

$\begin{bmatrix} \bar{1} & \bar{0} \\ \bar{0} & \bar{1} \end{bmatrix} + \begin{bmatrix} \bar{0} & \bar{1} \\ \bar{0} & \bar{1} \end{bmatrix} = \begin{bmatrix} \bar{1} & \bar{1} \\ \bar{0} & \bar{0} \end{bmatrix}$

Matriz booleana asociada a una relación

Dada relación binaria

\mathcal{R}

sobre un conjunto de n elementos

\{a_1,\dots,a_n\}

, para calcular la clausuara simétrica conviene representar la relación como matriz booleana definida mediante:

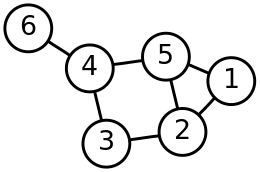
$B_\mathcal{R} = [b_{ij}]\quad \land \quad b_{ij} = \begin{cases} 1 & \mbox{si}\ a_i\mathcal{R}a_j\\ 0 & \mbox{si}\ \lnot a_i\mathcal{R}a_j \end{cases}$

Diagrama de un grafo con 6 vértices y 7 aristas.

El grafo no dirigido de la figura adjunta puede entenderse como una relación binaria. Dos elementos están relacionados si existe una línea que los una directamente. La matriz asociada a la relación binaria de conexión directa se llama matriz de incidencia, que es una matriz booleana que viene dada por:

$\begin{bmatrix} 0 & 1 & 0 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \end{bmatrix}$