LISTA DE PROBLEMAS

La modularidad es una medida de la estructura de redes o gráficos . Fue diseñado para medir la fuerza de la división de una red en módulos (también llamados grupos, grupos o comunidades). Las redes con alta modularidad tienen conexiones densas entre los nodos dentro de los módulos pero conexiones dispersas entre nodos en diferentes módulos. La modularidad se usa a menudo en los métodos de optimización para detectar la estructura de la comunidad en las redes. Sin embargo, se ha demostrado que la modularidad sufre un límite de resolución y, por lo tanto, no puede detectar comunidades pequeñas. Las redes biológicas, incluidos los cerebros de los animales, exhiben un alto grado de modularidad.

Motivación [ editar ]

Muchos problemas de importancia científica pueden representarse y estudiarse empíricamente utilizando redes. Por ejemplo, los patrones biológicos y sociales, la World Wide Web, las redes metabólicas, las redes alimentarias, las redes neuronales y las redes patológicas son problemas del mundo real que pueden representarse matemáticamente y estudiarse topológicamente para revelar algunas características estructurales inesperadas. ^[1]La mayoría de estas redes poseen una cierta estructura comunitaria que tiene una importancia sustancial en la construcción de un entendimiento sobre la dinámica de la red. Por ejemplo, una comunidad social estrechamente conectada implicará una tasa más rápida de transmisión de información o rumor entre ellos que una comunidad débilmente conectada. Por lo tanto, si una red está representada por una serie de nodos individuales conectados por enlaces que significan un cierto grado de interacción entre los nodos, las comunidades se definen como grupos de nodos densamente interconectados que solo están escasamente conectados con el resto de la red. Por lo tanto, puede ser imperativo identificar las comunidades en las redes, ya que las comunidades pueden tener propiedades muy diferentes, como el grado de nodo, el coeficiente de agrupamiento, la intermediación, la centralidad. ^[2]etc., del de la red promedio. La modularidad es una de esas medidas, que cuando se maximiza, conduce a la aparición de comunidades en una red determinada.

Definición [ editar ]

La modularidad es la fracción de los bordes que se encuentran dentro de los grupos dados menos la fracción esperada si los bordes se distribuyen al azar. El valor de la modularidad para gráficos no ponderados y no dirigidos reside en el rango$${\ displaystyle [-1 / 2,1]}. ^[3] Es positivo si el número de aristas dentro de los grupos excede el número esperado en función del azar. Para una división dada de los vértices de la red en algunos módulos, la modularidad refleja la concentración de bordes dentro de los módulos en comparación con la distribución aleatoria de enlaces entre todos los nodos, independientemente de los módulos.

Existen diferentes métodos para calcular la modularidad. ^[1] En la versión más común del concepto, la aleatorización de los bordes se realiza para preservar el grado de cada vértice. Considere una gráfica con$${\ displaystyle n} nodos y$${\ displaystyle m}enlaces ( bordes ) de modo que el gráfico se pueda dividir en dos comunidades utilizando una variable de pertenencia$${\ displaystyle s}. Si un nodo$${\ displaystyle v} pertenece a la comunidad 1, $${\ displaystyle s_ {v} = 1}, o si $${\ displaystyle v} pertenece a la comunidad 2, $${\ displaystyle s_ {v} = - 1}. Deje que la matriz de adyacencia para la red esté representada por$${\ displaystyle A}, dónde $${\ displaystyle A_ {vw} = 0} significa que no hay borde (sin interacción) entre nodos $${\ displaystyle v} y $${\ displaystyle w} y $${\ displaystyle A_ {vw} = 1}significa que hay un borde entre los dos. También por simplicidad consideramos una red no dirigida. Así$${\ displaystyle A_ {vw} = A_ {wv}}. (Es importante tener en cuenta que pueden existir múltiples aristas entre dos nodos, pero aquí evaluamos el caso más simple).

La modularidad Q se define entonces como la fracción de aristas que se encuentran dentro del grupo 1 o 2, menos el número esperado de aristas dentro de los grupos 1 y 2 para un gráfico aleatorio con la misma distribución de grados de nodo que la red dada.

El número esperado de aristas se calculará utilizando el concepto de un modelo de configuración . ^[4] El modelo de configuración es una realización aleatoria de una red particular. Dada una red con$${\ displaystyle n} nodos, donde cada nodo $${\ displaystyle v} tiene un grado de nodo $${\ displaystyle k_ {v}}, el modelo de configuración corta cada borde en dos mitades, y luego cada medio borde, llamado trozo , se vuelve a cablear aleatoriamente con cualquier otro trozo en la red (excepto él mismo), incluso permitiendo bucles automáticos (que ocurren cuando un trozo se vuelve a cablear a otro trozo del mismo nodo) y múltiples bordes entre los mismos dos nodos. Por lo tanto, aunque la distribución de grados de nodo del gráfico permanece intacta, el modelo de configuración da como resultado una red completamente aleatoria.

Número esperado de bordes entre nodos [ editar ]

Ahora considere dos nodos v y w , con grados de nodo$${\ displaystyle k_ {v}} y $${\ displaystyle k_ {w}}respectivamente, de una red cableada aleatoriamente como se describe anteriormente. Calculamos el número esperado de bordes completos entre estos nodos.

Deje que el número total de stubs en la red sea $${\ displaystyle l}:

$${\ displaystyle l = \ sum _ {u} k_ {u} = 2m}

( 1 )

Consideremos cada uno de los $${\ displaystyle k_ {v}}trozos de nodo v y crear variables indicadoras asociadas$${\ displaystyle I_ {i}} para ellos, $${\ displaystyle i = 1, \ ldots, k_ {v}}, con $${\ displaystyle I_ {i} = 1} si el trozo i-th se conecta a uno de los $${\ displaystyle k_ {w}}trozos de nodo w en este gráfico aleatorio particular. Si no lo hace, entonces su valor es 0. Dado que el trozo i-ésimo del nodo v puede conectarse a cualquiera de los$${\ displaystyle 2m-1} trozos restantes con igual probabilidad, y dado que hay $${\ displaystyle k_ {w}}trozos a los que se puede conectar asociado con el nodo w , evidentemente

$${\ displaystyle p (I_ {i} = 1) = E [I_ {i}] = {\ frac {k_ {w}} {2m-1}}}

El número total de bordes completos. $${\ displaystyle J_ {vw}}entre v y w es solo$${\ displaystyle J_ {vw} = \ sum _ {i} ^ {k_ {v}} I_ {i}}, entonces el valor esperado de esta cantidad es

$${\ displaystyle E [J_ {vw}] = E [\ sum _ {i} I_ {i}] = \ sum _ {i} ^ {k_ {v}} E [I_ {i}] = {\ frac { k_ {v} k_ {w}} {2m-1}}}

Muchos textos hacen las siguientes aproximaciones, para redes aleatorias con una gran cantidad de bordes. Cuando m es grande, sueltan la resta de 1 en el denominador de arriba y simplemente usan la expresión aproximada$${\ displaystyle {\ frac {k_ {v} k_ {w}} {2m}}}para el número esperado de aristas entre dos nodos. Además, en una red aleatoria grande, el número de auto-bucles y múltiples bordes es muy pequeño (se necesita referencia). Ignorar los bucles automáticos y los bordes múltiples permite suponer que hay como máximo un borde entre dos nodos. En ese caso,$${\ displaystyle J_ {vw}}se convierte en una variable indicadora binaria, por lo que su valor esperado también es la probabilidad de que sea igual a 1, lo que significa que se puede aproximar la probabilidad de que exista un borde entre los nodos v y w como$${\ displaystyle {\ frac {k_ {v} k_ {w}} {2m}}}.

Modularidad [ editar ]

Por lo tanto, la diferencia entre el número real de bordes entre el nodo $${\ displaystyle v} y $${\ displaystyle w} y el número esperado de bordes entre ellos es

$${\ displaystyle A_ {vw} - {\ frac {k_ {v} k_ {w}} {2m}}}

La suma de todos los pares de nodos da la ecuación para la modularidad, $${\ displaystyle Q}. ^[1]

$${\ displaystyle Q = {\ frac {1} {2m}} \ sum _ {vw} \ left [A_ {vw} - {\ frac {k_ {v} k_ {w}} {2m}} \ right] { \ frac {s_ {v} s_ {w} +1} {2}}}

( 3 )

Es importante tener en cuenta que la ecuación. 3 es válido para dividir solo en dos comunidades. La partición jerárquica (es decir, la partición en dos comunidades, luego las dos subcomunidades se dividieron en dos subcomunidades más pequeñas solo para maximizar Q ) es un posible enfoque para identificar múltiples comunidades en una red. Además, (3) puede generalizarse para particionar una red en comunidades c . ^[5]

$${\ displaystyle Q = {\ frac {1} {(2m)}} \ sum _ {vw} \ left [A_ {vw} - {\ frac {k_ {v} k_ {w}} {(2m)}} \ right] \ delta (c_ {v}, c_ {w}) = \ sum _ {i = 1} ^ {c} (e_ {ii} -a_ {i} ^ {2})}

( 4 )

donde e _ij es la fracción de aristas con vértices extremos en la comunidad i y la otra en la comunidad j :

$${\ displaystyle e_ {ij} = \ sum _ {vw} {\ frac {A_ {vw}} {2m}} 1_ {v \ in c_ {i}} 1_ {w \ in c_ {j}}}

y a _i es la fracción de extremos de bordes que están unidos a vértices en la comunidad i :

$${\ displaystyle a_ {i} = {\ frac {k_ {i}} {2m}} = \ sum _ {j} e_ {ij}}

Ejemplo de detección de comunidad múltiple [ editar ]

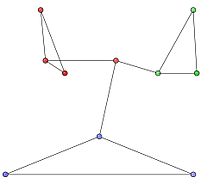
Consideramos una red no dirigida con 10 nodos y 12 aristas y la siguiente matriz de adyacencia.

Fig. 1. Red de muestra correspondiente a la matriz de adyacencia con 10 nodos, 12 aristas.

Fig. 2. Particiones de red que maximizan Q. Máximo Q = 0.4896

ID de nodo	1	2	3	4 4	5 5	6 6	7 7	8	9 9	10
1	0 0	1	1	0 0	0 0	0 0	0 0	0 0	0 0	1
2	1	0 0	1	0 0	0 0	0 0	0 0	0 0	0 0	0 0
3	1	1	0 0	0 0	0 0	0 0	0 0	0 0	0 0	0 0
4 4	0 0	0 0	0 0	0 0	1	1	0 0	0 0	0 0	1
5 5	0 0	0 0	0 0	1	0 0	1	0 0	0 0	0 0	0 0
6 6	0 0	0 0	0 0	1	1	0 0	0 0	0 0	0 0	0 0
7 7	0 0	0 0	0 0	0 0	0 0	0 0	0 0	1	1	1
8	0 0	0 0	0 0	0 0	0 0	0 0	1	0 0	1	0 0
9 9	0 0	0 0	0 0	0 0	0 0	0 0	1	1	0 0	0 0
10	1	0 0	0 0	1	0 0	0 0	1	0 0	0 0	0 0

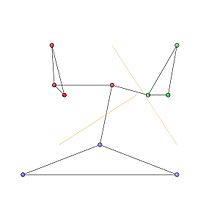
Las comunidades en el gráfico están representadas por los grupos de nodos rojo, verde y azul en la figura 1. Las particiones óptimas de la comunidad se representan en la figura 2.

Formulación matricial [ editar ]

Una formulación alternativa de la modularidad, útil particularmente en algoritmos de optimización espectral, es la siguiente. ^[1] Defina S _vr como 1 si el vértice v pertenece al grupo r y cero en caso contrario. Luego

$${\ displaystyle \ delta (c_ {v}, c_ {w}) = \ sum _ {r} S_ {vr} S_ {wr}}

y por lo tanto

$${\ displaystyle Q = {\ frac {1} {2m}} \ sum _ {vw} \ sum _ {r} \ left [A_ {vw} - {\ frac {k_ {v} k_ {w}} {2m }} \ right] S_ {vr} S_ {wr} = {\ frac {1} {2m}} \ mathrm {Tr} (\ mathbf {S} ^ {\ mathrm {T}} \ mathbf {BS}), }

donde S es la matriz (no cuadrada) que tiene elementos S _vr y B es la llamada matriz de modularidad, que tiene elementos

$${\ displaystyle B_ {vw} = A_ {vw} - {\ frac {k_ {v} k_ {w}} {2m}}.}

Todas las filas y columnas de la matriz de modularidad suman cero, lo que significa que la modularidad de una red no dividida también es siempre cero.

Para redes divididas en solo dos comunidades, una puede definir alternativamente s _v = ± 1 para indicar la comunidad a la que pertenece el nodo v , que luego conduce a

$${\ displaystyle Q = {1 \ over 4m} \ sum _ {vw} B_ {vw} s_ {v} s_ {w} = {1 \ over 4m} \ mathbf {s} ^ {\ mathrm {T}} \ mathbf {Bs},}

donde s es el vector de columna con elementos s _v . ^[1]

Esta función tiene la misma forma que el Hamiltoniano de un vidrio giratorio Ising , una conexión que ha sido explotada para crear algoritmos informáticos simples, por ejemplo, utilizando recocido simulado , para maximizar la modularidad. La forma general de la modularidad para un número arbitrario de comunidades es equivalente a un vidrio giratorio de Potts y también se pueden desarrollar algoritmos similares para este caso. ^[6]

Límite de resolución [ editar ]

La modularidad compara el número de bordes dentro de un clúster con el número esperado de bordes que uno encontraría en el clúster si la red fuera una red aleatoria con el mismo número de nodos y donde cada nodo mantiene su grado, pero los bordes se unen aleatoriamente. Este modelo nulo aleatorio supone implícitamente que cada nodo puede conectarse a cualquier otro nodo de la red. Sin embargo, esta suposición no es razonable si la red es muy grande, ya que el horizonte de un nodo incluye una pequeña parte de la red, ignorando la mayor parte. Además, esto implica que el número esperado de bordes entre dos grupos de nodos disminuye si aumenta el tamaño de la red. Por lo tanto, si una red es lo suficientemente grande, el número esperado de bordes entre dos grupos de nodos en el modelo nulo de modularidad puede ser menor que uno. Si esto pasa, un único borde entre los dos grupos sería interpretado por la modularidad como un signo de una fuerte correlación entre los dos grupos, y la optimización de la modularidad conduciría a la fusión de los dos grupos, independientemente de las características de los grupos. Entonces, incluso los gráficos completos débilmente interconectados, que tienen la mayor densidad posible de bordes internos y representan las mejores comunidades identificables, se fusionarían mediante la optimización de la modularidad si la red fuera lo suficientemente grande.^[7] Por esta razón, optimizar la modularidad en redes grandes no resolvería comunidades pequeñas, incluso cuando están bien definidas. Este sesgo es inevitable para métodos como la optimización de la modularidad, que se basan en un modelo nulo global. ^[8]

Métodos multirresolución [ editar ]

Hay dos enfoques principales que intentan resolver el límite de resolución dentro del contexto de modularidad: la adición de una resistencia r a cada nodo, en forma de bucle automático , que aumenta ( r> 0 ) o disminuye ( r <0 i=""> ) la aversión de los nodos para formar comunidades; ^[9] o la adición de un parámetro γ> 0 delante del término de caso nulo en la definición de modularidad, que controla la importancia relativa entre los enlaces internos de las comunidades y el modelo nulo. ^[6]Optimizando la modularidad para los valores de estos parámetros en sus respectivos rangos apropiados, es posible recuperar toda la mesoescala de la red, desde la macroescala en la que todos los nodos pertenecen a la misma comunidad, hasta la microescala en la que cada nodo forma su propia comunidad, de ahí el nombre de métodos multirresolución . Sin embargo, se ha demostrado que estos métodos tienen limitaciones cuando las comunidades son muy heterogéneas en tamaño.