En la teoría de grafos , una descomposición camino de un gráfico de G es, de manera informal, una representación de G como un "espesado" gráfico de ruta , [1] y la pathwidth de G es un número que mide la cantidad se espesó el camino para formar G . Más formalmente, una descomposición de ruta es una secuencia de subconjuntos de vértices de G de modo que los puntos finales de cada borde aparecen en uno de los subconjuntos y de manera que cada vértice aparece en una subsecuencia contigua de los subconjuntos, [2] y el ancho de ruta es uno menos que el tamaño del conjunto más grande en tal descomposición. Pathwidth también se conoce comoespesor del intervalo (uno menos que el tamaño máximo de la camarilla en un superógrafo de intervalo de G ), número de separación de vértices o número de búsqueda de nodo . [3]
El ancho de ruta y las descomposiciones de ruta son muy análogas al ancho de árbol y las descomposiciones de árbol . Desempeñan un papel clave en la teoría de los gráficos menores : las familias de gráficos que están cerrados bajo gráficos menores y no incluyen todos los bosques pueden caracterizarse por tener un ancho de ruta limitado [2] y los "vórtices" que aparecen en la teoría de la estructura general. para las familias de gráficos menores cerrados tienen ancho de ruta limitado. [4] Ancho de ruta, y gráficos de ancho de ruta limitado, también tienen aplicaciones en diseño VLSI , dibujo de gráficos y lingüística computacional .
Es NP-difícil encontrar el ancho de ruta de los gráficos arbitrarios, o incluso aproximarlo con precisión. [5] [6] Sin embargo, el problema es el parámetro manejable de parámetros fijos : probar si un gráfico tiene un ancho de ruta k puede resolverse en una cantidad de tiempo que depende linealmente del tamaño del gráfico pero superexponencialmente de k . [7] Además, para varias clases especiales de gráficos, como árboles , el ancho de ruta se puede calcular en tiempo polinómico sin dependencia de k . [8] [9] Muchos problemas en los algoritmos de gráficos pueden resolverse de manera eficiente en gráficos de ancho de ruta acotado, mediante el uso de programación dinámicaen una ruta de descomposición de la gráfica. [10] La descomposición del camino también se puede usar para medir la complejidad espacial de los algoritmos de programación dinámica en gráficos de ancho de árbol acotado .
Definición [ editar ]
En el primero de su famosa serie de artículos sobre grafos menores , Neil Robertson y Paul Seymour ( 1983 ) definen una descomposición de camino de un grafo G como una secuencia de subconjuntos X i de vértices de G , con dos propiedades:
- Para cada borde de G , existe un i tal que ambos extremos del borde pertenecen al subconjunto X i , y
- Por cada tres índices i ≤ j ≤ k , X i ∩ X k ⊆ X j .
La segunda de estas dos propiedades es equivalente a requerir que los subconjuntos que contienen cualquier vértice particular formen una subsecuencia contigua de toda la secuencia. En el lenguaje de los documentos posteriores en la serie de grafos menores de Robertson y Seymour, una descomposición de ruta es una descomposición de árbol ( X , T ) en la cual el árbol T subyacente de la descomposición es una gráfica de ruta .
El ancho de una descomposición de ruta se define de la misma manera que para las descomposiciones de árbol, como max i | X i | - 1, y la pathwidth de G es la anchura mínima de cualquier ruta-descomposición de G . La resta de uno del tamaño de X i en esta definición hace poca diferencia en la mayoría de las aplicaciones de ancho de ruta, pero se usa para hacer que el ancho de ruta de un gráfico de ruta sea igual a uno.
Caracterizaciones alternativas [ editar ]
Como describe Bodlaender (1998) , el ancho de ruta puede caracterizarse de muchas maneras equivalentes.
Pegar secuencias [ editar ]
Una descomposición trayectoria se puede describir como una secuencia de gráficos G i que se pegan juntos mediante la identificación de pares de vértices de gráficos consecutivos en la secuencia, de tal manera que el resultado de realizar todas estas gluings es G . Los gráficos G i pueden tomarse como las subgrafías inducidas de los conjuntos X i en la primera definición de descomposiciones de camino, con dos vértices en subgrafías inducidas sucesivas pegadas cuando son inducidas por el mismo vértice en G , y en la otra dirección uno puede recuperar los conjuntos X i como los conjuntos de vértices de los gráficos G i. El ancho de la descomposición del camino es entonces uno menor que el número máximo de vértices en uno de los gráficos G i . [2]
Grosor de intervalo [ editar ]
El ancho de ruta de cualquier gráfico G es igual a uno menos que el número de camarilla más pequeño de un gráfico de intervalo que contiene G como un subgrafo. [13] Es decir, para cada descomposición de ruta de G se puede encontrar una superposición de intervalo de G , y para cada supergrafía de intervalo de G se puede encontrar una descomposición de ruta de G , de modo que el ancho de la descomposición sea uno menos que la camarilla número del gráfico de intervalo.
En una dirección, supongamos que una descomposición camino de G se da. Entonces uno puede representar los nodos de la descomposición como puntos en una línea (en orden de ruta) y representar cada vértice v como un intervalo cerrado que tiene estos puntos como puntos finales. De esta manera, los nodos de descomposición de ruta que contienen v corresponden a los puntos representativos en el intervalo para v . El gráfico de intersección de los intervalos formados a partir de los vértices de G es un gráfico de intervalos que contiene G como un subgrafo. Sus máxima camarillas están dadas por los conjuntos de intervalos que contienen los puntos representativos, y su tamaño máximo clique es uno más el pathwidth de G .
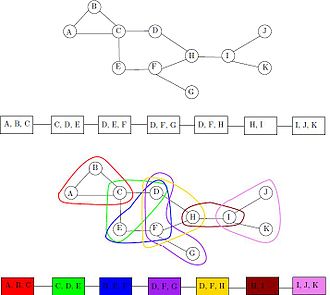
En la otra dirección, si G es un subgrafo de un gráfico de intervalo con el número de camarilla p + 1, entonces G tiene una descomposición de ruta de ancho p cuyos nodos están dados por las camarillas máximas del gráfico de intervalo. Por ejemplo, el gráfico de intervalos que se muestra con su representación de intervalos en la figura tiene una descomposición de ruta con cinco nodos, correspondientes a sus cinco camarillas máximas ABC , ACD , CDE , CDF y FG ; el tamaño máximo de la camarilla es tres y el ancho de esta descomposición del camino es dos.
Esta equivalencia entre el ancho del camino y el grosor del intervalo es muy similar a la equivalencia entre el ancho del árbol y el número mínimo de camarillas (menos uno) de un gráfico cordal del cual el gráfico dado es un subgrafo. Los gráficos de intervalo son un caso especial de los gráficos cordales, y los gráficos cordales se pueden representar como gráficos de intersección de subárboles de un árbol común generalizando la forma en que los gráficos de intervalo son gráficos de intersección de subtrayectos de una ruta.
Número de separación de vértices [ editar ]
Suponga que los vértices de un gráfico G están ordenados linealmente . Entonces, el número de separación de vértices de G es el número más pequeño s tal que, para cada vértice v , en la mayoría de los vértices s son anteriores a v en el orden pero que tienen v o un vértice posterior como vecino. El número de separación vértice de G es el número mínimo de separación vértice de cualquier ordenación lineal de G . El número de separación vértice se define por Ellis, Sudborough y Turner (1983) , y es igual a la pathwidth de G . [14] Esto se deduce de la equivalencia anterior con los números de camarilla del gráfico de intervalos: si G es un subgrafo de un gráfico de intervalos I , representado (como en la figura) de tal manera que todos los puntos finales del intervalo son distintos, entonces el orden de los puntos finales izquierdos del intervalos de I tiene el número de separación vértice uno menos que el número clique de I . Y en la otra dirección, a partir de un ordenamiento lineal de G se puede derivar una representación de intervalo en la que el punto final izquierdo del intervalo para un vértice v es su posición en el orden y el punto final derecho es la posición del vecino de v que viene último en el pedido.
Número de búsqueda de nodo [ editar ]
El juego de búsqueda de nodos en un gráfico es una forma de búsqueda-evasión en la que un conjunto de buscadores colabora para rastrear a un fugitivo que se esconde en un gráfico. Los buscadores se colocan en vértices del gráfico, mientras que el fugitivo puede estar en cualquier borde del gráfico, y la ubicación y los movimientos del fugitivo están ocultos para los buscadores. En cada turno, algunos o todos los buscadores pueden moverse (arbitrariamente, no necesariamente a lo largo de los bordes) de un vértice a otro, y luego el fugitivo puede moverse a lo largo de cualquier ruta en el gráfico que no pase a través de un vértice ocupado por el buscador. El fugitivo es atrapado cuando ambos puntos finales de su borde están ocupados por buscadores. El número de búsqueda de nodo de un gráfico es el número mínimo de buscadores necesarios para garantizar que se pueda garantizar que el fugitivo sea atrapado, sin importar cómo se mueva. ComoKirousis y Papadimitriou (1985) muestran que el número de búsqueda de nodo de un gráfico es igual a su espesor de intervalo. La estrategia óptima para los buscadores es mover los buscadores para que en turnos sucesivos formen los conjuntos de separación de un orden lineal con un número mínimo de separación de vértices.
Límites [ editar ]
Cada gráfico n- vértice con ancho de ruta k tiene como máximo k ( n - k + ( k - 1) / 2)) bordes, y el máximo ancho de ruta- k gráficos (gráficos a los que no se pueden agregar más bordes sin aumentar el ancho de ruta) tener exactamente esta cantidad de aristas. Un gráfico de ancho de ruta máximo k debe ser una ruta k o una oruga k , dos tipos especiales de árbol k . Un árbol k es un gráfico cordal con exactamente n - k camarillas máximas , cada una de las cuales contienek + 1 vértices; en unárbol k que no es en sí unacamarilla ( k + 1) , cada camarilla máxima separa el gráfico en dos o más componentes, o contiene un vértice de hoja único, un vértice que pertenece a una sola camarilla máxima. Un k -path es un k -tree con a lo sumo dos hojas, y una k -caterpillar es un k -tree que se puede dividir en un k -path y un conjunto de k- hojas cada una adyacente a un separador k -clique de Laruta k . En particular, los gráficos máximos de ancho de ruta uno son exactamente los árboles de oruga .[15]
Dado que las descomposiciones de ruta son un caso especial de descomposiciones de árbol, el ancho de ruta de cualquier gráfico es mayor o igual que su ancho de árbol . El ancho de ruta también es menor o igual que el ancho de corte , el número mínimo de bordes que cruzan cualquier corte entre vértices de menor y mayor número en una disposición lineal óptima de los vértices de un gráfico; Esto se debe a que el número de separación de vértices, el número de vértices de menor número con vecinos de mayor número, puede a lo sumo igual al número de bordes cortados. [16] Por razones similares, el ancho de corte es como máximo el ancho de ruta multiplicado por el grado máximo de los vértices en un gráfico dado. [17]
Cualquier bosque n- vértice tiene ancho de ruta O (log n ). [18] Porque, en un bosque, siempre se puede encontrar un número constante de vértices cuya eliminación deja un bosque que se puede dividir en dos subpoblaciones más pequeñas con un máximo de 2 n / 3 vértices cada una. Una disposición lineal formada mediante la partición recursiva de cada uno de estos dos sub-bosques, colocando los vértices de separación entre ellos, tiene un número de búsqueda de vértices logarítmicos. La misma técnica, aplicada a la descomposición en árbol de un gráfico, muestra que, si el ancho de árbol de un gráfico de n -vértices G es t , entonces el ancho de ruta de G es O ( t log n) [19] Dado que los gráficos del plano exterior , los gráficos en serie y en paralelo y los gráficos de Halin tienen un ancho de árbol acotado, todos también tienen, como máximo, un ancho de ruta logarítmico.
Así como sus relaciones con treewidth, pathwidth también está relacionada con clique-anchura y cutwidth , a través de gráficos de líneas ; el gráfico lineal L ( G ) de un gráfico G tiene un vértice para cada borde de G y dos vértices en L ( G ) son adyacentes cuando los dos bordes correspondientes de G comparten un punto final. Cualquier familia de gráficos tiene un ancho de ruta limitado si y solo si sus gráficos de línea tienen un ancho de camarilla lineal acotado, donde el ancho de camarilla lineal reemplaza la operación de unión disjunta del ancho de camarilla con la operación de unir un único vértice nuevo. [20]Si un gráfico conectado con tres o más vértices tiene un grado máximo de tres, entonces su ancho de corte es igual al número de separación de vértices de su gráfico lineal. [21]
En cualquier gráfico plano , el ancho de ruta es como máximo proporcional a la raíz cuadrada del número de vértices. [22] Una forma de encontrar una descomposición de ruta con este ancho es (de manera similar a la descomposición de ruta de ancho logarítmico de los bosques descritos anteriormente) usar el teorema del separador plano para encontrar un conjunto de vértices O ( √ n ) la eliminación de que separa el gráfico en dos subgrafías de como máximo 2 n / 3 vértices cada una, y concatena descomposiciones de camino construidas recursivamente para cada una de estas dos subgrafías. La misma técnica se aplica a cualquier clase de gráficos para los cuales se cumple un teorema separador similar. [23]Dado que, al igual que los gráficos planos, los gráficos en cualquier familia de gráficos menor cerrada fija tienen separadores de tamaño O ( √ n ), [24] se deduce que el ancho de ruta de los gráficos en cualquier familia menor cerrada fija es nuevamente O ( √ n ) Para algunas clases de gráficos planos, el ancho de ruta del gráfico y el ancho de ruta de su gráfico dual deben estar dentro de un factor constante entre sí: los límites de esta forma son conocidos para los gráficos de plano externo biconconectados [25] y para los gráficos poliédricos. [26] Para los gráficos planos conectados a 2, el ancho de ruta del gráfico dual es menor que el ancho de ruta del gráfico lineal. [27] Permanece abierto si el ancho de ruta de un gráfico plano y su dual siempre están dentro de un factor constante entre sí en los casos restantes.
En algunas clases de gráficos, se ha demostrado que el ancho de ruta y el ancho del árbol son siempre iguales entre sí: esto es cierto para los cográficos , [28] gráficos de permutación , [29] los complementos de los gráficos de comparabilidad , [30] y los gráficos de comparabilidad de órdenes de intervalo . [31]
| Problema no resuelto en matemáticas : (Más problemas no resueltos en matemáticas) |
En cualquier gráfico cúbico , o más generalmente en cualquier gráfico con vértice máximo de grado tres, el ancho de ruta es como máximo n / 6 + o ( n ), donde n es el número de vértices en el gráfico. Existen gráficos cúbicos con ancho de ruta 0.082 n , pero no se sabe cómo reducir esta brecha entre este límite inferior y el límite superior n / 6.



No hay comentarios:
Publicar un comentario