EPÓNIMOS

Epónimos relacionados con la economía

El Equilibrio de Radner es un concepto económico definido por el economista Roy Radner en el contexto de equilibrio general.¹ El concepto es una extensión del equilibrio de Arrow-Debreu y la base para el primer modelo consistente de mercados incompletos.²

El cambio con el marco del modelo Arrow-Debreu es de dos tipos: (1) la incertidumbre se modela explícitamente a través de una estructura de árbol (o filtración equivalente) que va transformándose con el paso del tiempo y la resolución de la incertidumbre explícita, (2) la viabilidad presupuestaria ya no se define como la asequibilidad sino a través del comercio explícito de los instrumentos financieros. Los instrumentos financieros se utilizan para permitir que los seguros y transferencias de riqueza inter-temporales en los mercados al contado en cada nodo del árbol. Los agentes económicos se enfrentan a una secuencia de conjuntos presupuestarios, uno en cada fecha del estado.

La parte de la viabilidad presupuestaria introduce el concepto de mercados incompletos, formulados en términos de la demanda exterior neta, el conjunto del presupuesto está contenido en un espacio medio de intersección del cono positivo de bienes contingentes a la demanda exterior neta cero solamente (esto se llama ausencia de arbitraje). Esto es porque sin costos de transacción los agentes demandará una cantidad infinita de cualquier transacción que prometa un consumo positivo en algún estado y una transacción neta no negativa en contra de cualquier otro bien y estado. Este espacio de media, que contiene el conjunto del presupuesto y que lo separa del cono de almuerzo gratis, corresponde a una media línea de precios positivos. Sin embargo, si no potencialmente suficientes instrumentos están presentes, el espacio medio lleno no puede ser atravesado por el comercio de los instrumentos y los presupuestos establecidos pueden ser estrictamente menor. En unos mercados tales configuración se dice que son incompletas, y hay varias maneras de separar el conjunto del presupuesto del cono positivo (a veces llamado el cono-almuerzo gratis). Esto significa que varios sistemas de precios se vuelven admisible.

En un equilibrio de Radner como en un equilibrio de Arrow-Debreu bajo incertidumbre, se utiliza la previsión consensuada perfecta. Es lo que se llama un modelo de expectativas racionales.

• La extensión de los modelos básicos de Equilibrio General basados en la obra de Walras a una Economía con Incertidumbre fue realizada por Arrow (1957), siendo Debreu (1959) quien inició las consideraciones intertemporales. Estas primeras formulaciones del Equilibrio General Dinámico con Incertidumbre se conocen como Complete Contingent Claims Equilibrium, esto es Equilibrio Completo de Contratos Contingentes, o bien simplemente como Equilibrio Arrow-Debreu, y se caracterizan por suponer una única apertura de mercados, presentes y futuros, en el periodo inicial. Básicamente, el Equilibrio General formulado según el concepto de Equilibrio Arrow-Debreu es un equilibrio walrasiano en el cual las mercancías son diferentes en el tiempo y según el estado de la naturaleza que acontece.
  Fue también Arrow en ese mismo trabajo quien planteó una segunda definición de equilibrio general, conocida como Security-Spot Market Equilibrium o Equilibrio de Mercados Secuenciales, en la cual los mercados abren y cierran periodo tras periodo. Esta primera definicióon de Arrow de equilibrio general según el concepto de Mercados Secuenciales es en esencia un Equilibrio Arrow-Debreu obtenido comerciando en cada periodo de tiempo en una determinada clase de activos, y ha dado lugar al generalizar sus supuestos en torno a la información y a los activos a una nueva noción de equilibrio general conocida como Equilibrio de Radner, denominado así por ser fundamentalmente obra de Radner (1968).
  Junto a estas dos definiciones existe una tercera basada en el Principio de Optimalidad de Bellman, denominada Equilibrio Recursivo, y que es en ciertas condiciones equivalente al Equilibrio de Radner. Esta nueva formulación está basada en el hecho de que en el equilibrio general competitivo, los individuos maximizan su utilidad, presentando esta utilidad máxima bajo ciertos supuestos una propiedad invariante periodo tras periodo, de forma tal que el Equilibrio de Radner da origen a un problema que se repite en el tiempo. Básicamente, el Equilibrio Recursivo es un Equilibrio de Radner bajo una diferente formulación matemática, que va a permitir interesantes desarrollos teóricos y prácticos y que ha sido da amplia aplicación desde la obra inicial de Bellman.
  Las relaciones entre estas tres definiciones ha sido estudiada en diferentes marcos y de hecho forma parte subyacente de la mayoría de trabajos en Equilibrio General Dinámico con Incertidumbre. Sin embargo, para las dos primeras definiciones no existía un trabajo que pudiera aplicarse con generalidad a una economía con producción, puesto que la práctica totalidad de resultados hacían referencia a una economía de intercambio. Este no era el caso de las dos segundas definiciones, cuyas relaciones han sido objeto de numerosos estudios.
  En cuanto a las propiedades del Equilibrio, el Primer y Segundo Teoremas del Bienestar fueron primeramente estudiados en tiempo finito por Debreu (1959) y Arrow y Debreu (1954), encontrándose los fundamentos de la teoría a aplicar con dimensiones infinitas en Bewley (1976) y Mas-Colell y Zame (1991). Otras propiedades como la inexistencia de arbitraje fueron analizadas por Ross (1978) y por Chamberlain y Rothschild (1983).
  Estos puntos eminentemente teóricos del Equilibrio General Dinámico con Incertidumbre y otros afines son desarrollados en la tesis. En el Capítulo 2 se estudian exhaustivamente las relaciones entre las dos primeras definiciones de Equilibrio General para una Economía con Producción sumamente genérica así como las propiedades del Equilibrio General Competitivo, haciendo especial hincapié en los mercados de activos, residiendo la principal aportación en la elaboración de un modelo plurisectirial en la producción y en el establecimiento de una equivalencia entre las dos definiciones que es susceptible de ser aplicada para la práctica totalidad de economías con Incertidumbre. El único requisito que se exige es que los mercados sean completos, entendiendo éstos como aquellos que permiten cubrirse totalmente contra el riesgo. Como se ha dicho el modelo planteado es sumamente genérico, consistiendo en una ampliación del Modelo de Brock (1982) para una Economía de Producción, el cual a su vez está basado en el Modelo de Lucas (1978) para una Economía de Intercambio.
  Nuestras definiciones de Equilibrio Arrow-Debreu y de Equilibrio de Radner son una extensión de las existentes en tiempo finito en Magill and Shafer (1991), en un entorno de completa certidumbre en Kehoe (1991) y en una economía con incertidumbre en Radner (1991), las cuales a su vez están basadas en las definiciones ya clásicas de Arrow and Hahn (1971) y Debreu (1959). El referente más inmediato se encuentra en Mas-Colell, Whinston y Green (1995) y en Altug y Labadie (1994). Todos estos trabajos, en tiempo finito, proporcionan las de los Teoremas de Equivalencia establecidos en el Capítulo 2 entre el Equilibrio Arrow-Debreu y el Equilibrio de Radner. La aportación fundamental de la tesis en estos puntos es la consideración de modelos amplios con varios sectores de producción en un horizonte temporal infinito. Para estos teoremas, las líneas demostrativas son una ampliación de las realizadas en tiempo finito y para una Economía de Intercambio en Arrow (1954) y en Mas-Colell, Whinston y Green (1995).
  Respecto a las propiedades del Equilibrio General, estudiadas en el Capítulo 2, las demostraciones del Primer y Segundo Teoremas del Bienestar siguen de cerca las contenidas en Arrow and Hahn (1971) y en Mas-Colell, Whinston y Grenn (1995) para dimensiones finitas, habiéndose consultado Bewley (1976), Mas-Collell (1986), Mas-Colell y Zame (1991), Luenberger (1969) y Wilansky (1978) para adecuarlas a nuestros modelos con producción y a un horizonte temporal infinito. La inexistencia de arbitraje se concluye con los mismos argumentos apuntados en Ross (1978), siendo las restantes propiedades acerca de la acotación en las inversiones/desinversiones y en los precios de los activos novedosas.
  Una de las principales aportaciones de la tesis es la obtención de un conjunto de condiciones suficientes que garantizan la existencia de mercados completos, de carácter tecnológico, y que hacen innecesarias las habituales basadas en la existencia de un grado suficiente de heterogeneidad de los consumidores.

Modelos Plurisectoriales en Equilibrio General Dinámico con Producción e Incertidumbre

• Desde que Bellman sentara en su obra Dynamic Programming las bases para el enfoque iterativo del Equilibrio Dinámico, éste ha ido ganando constantemente importancia hasta constituirse en la técnica central a aplicar en el Equilibrio General Dinámico tanto con incertidumbre como sin ella. Muestra son los Modelos Neoclásicos de Crecimiento, los Modelos de Ciclos Reales o los Cash-in-Advance Models, por citar los ejemplos más relevantes.
  El éxito de la técnica iterativa en la Teoría del Equilibrio General Dinámico descansa en su evidente simpleza formal, sus ventajas computacionales y en una equivalencia con el Equilibrio de Radner relativamente sencilla de obtener y ampliamente estudiada. No obstante, también presenta inconvenientes, provenientes del paso a la agregación, implícito en la mayoría de modelos que aplican la ténica recursiva, y de los restrictivos supuestos en torno a la incertidumbre, que van más allá de los adoptados en los Equilibrios Arrow-Debreu y de Radner, de por sí limitativos.
  Por otra parte, este método recursivo conjuga aplicaciones prácticas y teóricas, y ambas son desarrolladas en la tesis. Así por ejemplo, si la equivalencia entre las dos primera definiciones de Equilibrio permite extraer conclusiones respecto a la optimalidad, la existencia del equilibrio o la imposibilidad del arbitraje, la equivalencia respecto al Equilibrio Recursivo arroja luz sobre cuestiones como las primas al riesgo, separabilidad de la función de utilidad o variables determinantes del bienestar. Todos estos temas son desarrollados en el Capítulo 3 donde además se fundamenta el paso a la agregación. Se comienza introduciendo un tipo especial de preferencias que bajo condiciones bastante generales permiten el paso a la agregación, y a continuación se demuestra detalladamente para nuestro modelo concreto la equivalencia entre el Equilibrio de Radner y el Equilibrio Recursivo y el consiguiente Problema del Planificador Social, siguiéndose los conceptos teóricos generales de Stokey-Lucas con Prescott (1989). Una vez obtenida la equivalencia se concluye la existencia de primas al riesgo y una versión para el consumidor representativo del teorema de Modigliani-Miller. Estos resultados son dada la generalidad de las demostraciones y de los modelos de más amplia aplicación que los ya existentes en la literatura, al igual que el paso a a la agregación, basado en Rubinstein (1974) pero bajo hipótesis más amplias. Esta es la aportación más relevante de la tesis en lo que respecta al enfoque iterativo desde la perspectiva teórica. Por ejemplo, los Teoremas de Agregación no requieren de funciones de utilidad separables y aditivas entre consumo presente y riqueza futura, algo que sí se exige en Rubinstein (1974), y las demostraciones de la existencia de primas al riesgo se realizan bajo una especificación de la riqueza de los individuos más amplia de lo habitual. El Capítulo 3 concluye con la obtención de un Modelo de Ciclos Reales con Mercados Completos novedoso, con varios sectores productivos, y con la incorporación rigurosa a través de una modificación en las funciones de producción de los mercados de acciones.
  Finalmente, el Capítulo 4 se dedica a la aplicación práctica del modelo. Se construye un programa de ordenador y se simula un modelo teórico bajo diferentes entornos estocásticos, computándose los estados estacionarios y realizándose simulaciones de los procesos de ajuste dinámico. El modelo simulado se corresponde con el estudiado en el Capítulo 3 y presenta todas las ventajas derivadas de su fundamentación microeconómica, con lo cual queda abierta la posibilidad de estudio de procesos dinámicos de ajuste ante perturbaciones en los distintos sectores productivos de la economía. Utilizando el algoritmo de programación dinámica se elaboró en lenguaje GAUSS un programa sumamente flexible con un total de 21 parámetros. Estos parámetros, susceptibles de calibración, son los correspondientes a la Economía de Producción del Capítulo 3 con dos tecnologías, y representan los denominados fundamentos del Problema del Planificador Social, esto es los gustos del consumidor representativo, las características de las tecnologías y las creencias y perturbaciones tecnológicas. Estos dos últimos elementos son precisamente los sometidos a cambio, analizándose los efectos subsiguientes sobre los mercados de activos. A este respecto, la computación de los estados estacionarios muestra una concordancia total con los resultados teóricos clásicos, a los cuales se suman otros novedosos relacionados con las fluctuaciones cíclicas en los stocks de capital y en el producto total.

Los Mercados de Activos

• Ya desde los primeros trabajos de Arrow y Debreu en la Teoría del Equilibrio General Dinámico con Incertidumbre tuvieron un papel central los mercados de activos, algo por otra parte lógico al encontrarnos en un marco dinámico donde existe riesgo. La literatura en torno a los mercados de activos continuó profusamente, siendo particularmente importantes los trabajos de Lucas (1978) y Brock (1982).
  Precisamente los mercados de activos es uno de los temas centrales de esta tesis, y concretamente los mercados de activos denominados completos. Aceptando la existencia de mercados de activos que permiten cubrirse contra todas las situaciones de riesgo, esto es dentro de un marco ideal de competencia perfecta donde existen mercados para todas las mercancías, en los Capítulos 2 y 3 se analizan exhaustivamente todas las implicaciones de esta hipótesis central, realizándose en el Capítulo 4 una serie de ejercicios prácticos. De hecho es en este campo donde se obtienen los principales resultados tanto teóricos como simulados. Así ocurre, por ejemplo, con propiedades como la ausencia de arbitraje, la acotación en las inversiones/desinversiones y en los precios de los activos o la existencia de primas al riesgo a un nivel teórico, y con las conclusiones en torno a los stocks de capital y a los precios de los activos en el Capítulo dedicado a la simulación del Modelo de Ciclos Reales con Mercados Completos. Asimismo y como queda reflejado en la conclusión de la tesis, buena parte de las futuras aplicaciones se centran en los mercados de activos, tanto a nivel teórico como computacional.

El coeficiente de Gini es una medida de la desigualdad ideada por el estadístico italiano Corrado Gini. Normalmente se utiliza para medir la desigualdad en los ingresos, dentro de un país, pero puede utilizarse para medir cualquier forma de distribución desigual. El coeficiente de Gini es un número entre 0 y 1, en donde 0 se corresponde con la perfecta igualdad (todos tienen los mismos ingresos) y donde el valor 1 se corresponde con la perfecta desigualdad (una persona tiene todos los ingresos y los demás ninguno).

El índice de Gini es el coeficiente de Gini expresado en porcentaje y es igual al coeficiente de Gini multiplicado por 100.

Aunque el coeficiente de Gini se utiliza sobre todo para medir la desigualdad en los ingresos, también puede utilizarse para medir la desigualdad en la riqueza. Este uso requiere que nadie disponga de una riqueza neta negativa.

Mapa esquemático de países según su coeficiente de Gini. Vea el listado completo en Anexo:Países por igualdad de ingreso.

     < 0,20     0,20 ↔ 0,24     0,25 ↔ 0,29     0,30 ↔ 0,34     0,35 ↔ 0,39     0,40 ↔ 0,44
     0,45 ↔ 0,49     0,50 ↔ 0,54     0,55 ↔ 0,59     ≥ 0,60

Definición

Diagrama que muestra el área acomprendida entre la curva de Lorenz y la bisectriz del cuadrado, dicha área es proporcional al coeficiente de Gini.

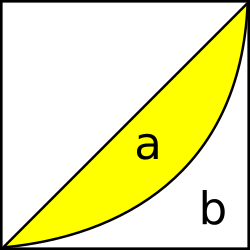
El coeficiente de Gini se calcula como una proporción de las áreas en el diagrama de la curva de Lorenz. Si el área entre la línea de perfecta igualdad y la curva de Lorenz es a, y el área por debajo de la curva de Lorenz es b, entonces el coeficiente de Gini es a/(a+b).

Esta proporción se expresa como porcentaje o como equivalente numérico de ese porcentaje, que es siempre un número entre 0 y 1. El coeficiente de Gini se calcula a menudo con la Fórmula de Brown, que es más práctica:

Donde:

• G: Coeficiente de Gini
• X: Proporción acumulada de la variable población
• Y: Proporción acumulada de la variable ingresos

De forma resumida, la Curva de Lorenz es una gráfica de concentración acumulada de la distribución de la riqueza superpuesta a la curva de la distribución de frecuencias de los individuos que la poseen, y su expresión en porcentajes es el índice de Gini.

Propiedades

• Todas las curvas de Lorenz pasan por los puntos (0,0) y (1,1). A mayor índice de Gini se tiene una mayor desigualdad. Si dos curvas de Lorenz se cruzan entre sí, se recomienda no sacar conclusiones visualmente pues pueden ser engañosas; es mejor comparar la desigualdad que representan, calculando primero los índices de Gini correspondientes a cada curva.
• Para determinar el área entre la curva de Lorenz y la línea de perfecta equidad, lo ideal es calcular una integral definida, pero a veces no se conoce la definición explícita de la curva de Lorenz, por lo que es interesante utilizar otras fórmulas con un número finito de sumandos.
• Las propiedades del índice de Gini son comparables con las del cuadrado del coeficiente de variación.¹
• Empíricamente, la renta de muchos países se aproxima a una distribución Gamma (con parámetro k < 5), lo cual lleva a los índices de Gini observados entre 0,50 y 0,25. Los países con índices superior a 0,50 tienen una distribución aún más desigual que la distribución exponencial.