curva de Hilbert (también conocida como la curva que recubre el plano de Hilbert) es una curva fractal continuaque recubre el plano descrita inicialmente por el matemático alemán David Hilbert en 1891,1 como una variante de las curvas que recubren el plano descubiertas por Giuseppe Peano en 1890.2
Debido a que recubre el plano, su dimensión de Hausdorff-Besicovitch es  (precisamente, su imagen es el cuadrado unitario, cuya dimensión es 2 en cualquier definición de dimensión; su gráfico es un conjunto compacto homeomórfico al intervalo cerrado de la unidad, con una dimensión de Hausdorff de 2).
(precisamente, su imagen es el cuadrado unitario, cuya dimensión es 2 en cualquier definición de dimensión; su gráfico es un conjunto compacto homeomórfico al intervalo cerrado de la unidad, con una dimensión de Hausdorff de 2).
 (precisamente, su imagen es el cuadrado unitario, cuya dimensión es 2 en cualquier definición de dimensión; su gráfico es un conjunto compacto homeomórfico al intervalo cerrado de la unidad, con una dimensión de Hausdorff de 2).
(precisamente, su imagen es el cuadrado unitario, cuya dimensión es 2 en cualquier definición de dimensión; su gráfico es un conjunto compacto homeomórfico al intervalo cerrado de la unidad, con una dimensión de Hausdorff de 2).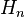 es la
es la  ésima aproximación al límite de la curva. La distancia euclidiana de
ésima aproximación al límite de la curva. La distancia euclidiana de 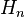 es
es  , i.e., crece exponencialmente con
, i.e., crece exponencialmente con  , a la vez que está siempre contenida en un cuadrado de área finita.
, a la vez que está siempre contenida en un cuadrado de área finita.
Primeros 8 pasos para construir la curva de Hilbert
Imágenes
Aplicaciones y algoritmos de correspondencia
Tanto la curva de Hilbert original como sus aproximaciones discretas son útiles porque proveen una correspondencia entre el espacio 1D y 2D que conserva bastante bien la localidad. Si (x,y) son las coordenadas de un punto dentro del cuadrado unitario, y d es la distancia a lo largo de la curva cuando se llega a ese punto, entonces los puntos que tienen distancias cercanas a d también tienen valores cercanos a (x ,y). Lo contrario no siempre puede ser cierto, ya que puntos con coordenadas (x, y) cercanas, pueden tener valores de d muy alejados. Esto es inevitable cuando se asigna un espacio 2D a un espacio 1D. Sin embargo, la curva de Hilbert consigue mantener bastante bien los valores de d cercanos gran parte del tiempo. Así que las asignaciones en ambas direcciones mantienen bastante bien la localidad.
Debido a esta propiedad de localidad, la curva de Hilbert se utiliza en la informática. Por ejemplo, el rango de las direcciones IP usadas por equipos puede ser representado gráficamente en una imagen utilizando la curva de Hilbert. El código para generar la imagen tendría que hacer una correspencia de 2D a 1D para encontrar el color de cada píxel y la curva de Hilbert se utiliza a veces, ya que mantiene direcciones IP similares cerca entre sí en la imagen. Una fotografía en escala de grises se puede convertir en una imagen en blanco y negro interpolada usando umbrales, con la cantidad sobrante de cada píxel añadida al siguiente pixel a lo largo de la curva de Hilbert. El código para hacer esto hace una correspondencia de 1D a 2D, y la curva de Hilbert se usa a veces porque no crea los patrones de distracción que serían visibles al ojo si el orden fuera simplemente de izquiera a derecha en cada fila de píxeles. Las curvas de Hilbert en dimensiones superiores son una generalización de loscódigos de Gray, que se utilizan para propósitos similares, por las mismas razones. Para bases de datos multidimensionales, se ha propuesto el uso del orden de Hilbert en lugar del Z orden porque se comporta mejor preservando la localidad.
Dada esta variedad de aplicaciones, es útil disponer de algoritmos de correspondencia en ambas direcciones. En muchos lenguajes de programación, esto se implementa mejor usando iteración en vez de recursividad. El siguiente código en C realiza las correspondencias en ambas direcciones utilizando iteración y operaciones de bits en lugar de recursividad. Supone un cuadrado dividido en n por n celdas, siendo n una potencia de 2, con coordenadas enteras, con (0,0) en la esquina inferior izquierda y (n -1, n-1) en la esquina superior derecha, y una distanciad que comienza en 0 en la parte inferior de la esquina inferior izquierda y llega a  en la esquina inferior derecha.
en la esquina inferior derecha.
 en la esquina inferior derecha.
en la esquina inferior derecha.//convierte (x,y) a d
int xy2d (int n, int x, int y) {
int rx, ry, s, d=0;
for (s = n/2; s > 0; s /= 2) {
rx = (x & s) > 0;
ry = (y & s) > 0;
d += s * s * ((3 * rx) ^ ry);
rot(s, &x, &y, rx, ry);
}
return d;
}
//convierte d a (x,y)
void d2xy(int n, int d, int *x, int *y) {
int rx, ry, s, t=d;
*x = *y = 0;
for (s = 1; s < n; s *= 2) {
rx = 1 & (t/2);
ry = 1 & (t ^ rx);
rot(s, x, y, rx, ry);
*x += s * rx;
*y += s * ry;
t /= 4;
}
}
//rotar/voltear un cuadrante apropiadamente
void rot(int n, int *x, int *y, int rx, int ry) {
int t;
if (ry == 0) {
if (rx == 1) {
*x = n-1 - *x;
*y = n-1 - *y;
}
t = *x;
*x = *y;
*y = t;
}
}
Se usan las siguientes convenciones de C: el símbolo & es un AND binario, el símbolo ^ es un XOR binario, el operador += añade a una variable, y el operador /= divide una variable. El manejo de booleanos en C supone que en xy2d, la variable rx se pone a 0 o 1 para representar al bit s de x, y análogamente para ry.
La función xy2d trabaja de arriba abajo, comenzando con el bit más significativo de x e y, y construyendo los bits más significativos de d primero. La función d2xy trabajan en orden inverso, comenzando con los bits menos significativos de d, y construyendo x e y comenzando por los bits menos significativos. Ambas funciones usan la función de rotación para rotar e invertir el sistema de coordenadas (x,y) apropiadamente.
Los dos algoritmos de correspondencia funcionan de manera similar. El cuadrado completo se ve como compuesto por cuatro regiones, dispuestas en 2 por 2. Cada región está compuesta por cuatro regiones más pequeñas, y así sucesivamente, para una serie de niveles. En el nivel s, cada región consiste en s por s celdas. Hay un simple bucle FOR que recorre los niveles. En cada iteración, se añade una cantidad a d o x e y, determinada por en cuál de las cuatro regiones se encuentra en el nivel actual. La región actual de los 4 es (rx, ry), donde rx y ry son 0 o 1. Por lo que consume 2 bits de entrada, (ya sean 2 de d o cada 1 de x e y), y genera dos bits de salida. También invoca a la función de rotación de manera que (x, y) sean los adecuados para el siguiente nivel, en la siguiente iteración. Para xy2d, se inicia en el nivel superior del cuadrado completo y se abre camino hasta el nivel más bajo de las celdas individuales. Para d2xy, comienza en la parte inferior de las celdas, y trabaja para incluir todo el cuadrado.
Representación como un sistema de Lindenmayer
La Curva de Hilbert se puede expresar como un sistema de reescritura (Sistema-L).
- Alfabeto : A, B
- Constantes : f, l, r
- Axioma : A
- Reglas de producción:
- A → l B fr A f A rf B l
- B → r A fl B f B lf A r
Donde, f significa "dibuja hacia delante", l significa "gira a la izquierda 90°", y r significa "gira a la derecha 90°" (véase gráficas tortuga).
Arthur Butz3 diseñó un algoritmo para calcular la curva de Hilbert en varias dimensiones.
Graphics Gems II4 discute la coherencia de la curva de Hilbert, y provee una implementación.
Dibujemos un cuadrado de lado unidad. Lo dividimos en cuatro partes iguales. Unimos los centros de los cuatro cuadrados como muestra la figura inferior. Volvemos a dividir cada cuadrado en cuatro cuadrados idénticos y unimos de nuevo los centros de todos los cuadrados mediante una sola curva siguiendo el patrón mostrado en el segundo paso de la figurada inferior (Orden 2). Observemos cómo la curva serpentea comenzando en el cuadrado superior izquierdo y acabando en el cuadrado superior derecho. En la figura alcanzamos la tercera iteración. Con paciencia, repetimos el procedimiento infinitamente. En el límite obtendremos la curva de Hilbert.
La curva tiene la curiosa propiedad de ser una curva continua que pasa por todos los puntos del cuadrado unidad. Pero, si una curva es unidimensional, ¿cómo es posible que llene un espacio bidimensional? ¿Podemos decir entonces que esta curva es también bidimensional?
A finales del siglo XIX Cantor intentaba encontrar un conjunto infinito de un número de elementos mayor que el intervalo [0, 1]. Parecía obvio que el cuadadro de lado unidad poseía más puntos. Pero de forma contraintuitiva demostró que eran conjuntos del mismo "tamaño". Se disponía entonces de una manera de establecer una biyección entre los puntos de un segmento y un cuadrado, aunque esta función no era continua. Otros matemáticos como Giuseppe Peano y Hilbert desarrollaron funciones continuas del intervalo [0, 1] al cuadrado unidad de modo que se establecieran correspondencias exhaustivas (hay puntos en el cuadrado unidad que poseen más de una imagen en el intervalo unidad), es decir, perdiendo la biyección. Tales funciones se denominaron curvas que llenan el espacio (space-filling curves). ¿Existían correspondencias continuas y biyectivas? ¿Si fuera así el concepto de dimensión quedaría en entredicho?
En 1911 Luitzen Brouwer probó que no existen tales correspondencias, biyectivas y continuas al mismo tiempo. La dimensión era un invariante topológico y no podía ser alterada por deformaciones continuas. Como resultado se llegó a una definición rigurosa de dimensión topológica del espacio. Como veremos en el siguiente capítulo otra línea de razonamiento llevó a otras definiciones de dimensión.
Abajo podemos observar otro ejemplo: la curva de Peano. De hecho, Peano la descubrió en 1891 y Hilbert hizo una variación sobre ella (la curva de Hilbert) un año después.
curva de Lissajous, también conocida como figura de Lissajous o curva de Bowditch, es la gráfica del sistema de ecuaciones paramétricas correspondiente a la superposición de dos movimientos armónicos simples en direcciones perpendiculares:
Esta familia de curvas fue investigada por Nathaniel Bowditch en 1815 y después, con mayores detalles, por Jules Antoine Lissajous.
En mecánica clásica, la trayectoria de un movimiento armónico complejo bidimensional es una curva de Lissajous.
Mecánica Gravitatoria
(pendiente de editar).
(relacionado con Puntos de Lagrange).
Propiedades
La apariencia de la figura es muy sensible a la relación  , esto es, la relación entre las frecuencias de los movimientos en x e y. Para un valor de 1, la figura es una elipse, con los casos especiales del círculo (A = B, δ = π/2 radianes) y de las rectas (δ = 0) incluidos. Otra de las figuras simples de Lissajous es la parábola (a/b = 2, δ = π/2). Otros valores de esta relación producen curvas más complicadas, las cuales sólo son cerradas si
, esto es, la relación entre las frecuencias de los movimientos en x e y. Para un valor de 1, la figura es una elipse, con los casos especiales del círculo (A = B, δ = π/2 radianes) y de las rectas (δ = 0) incluidos. Otra de las figuras simples de Lissajous es la parábola (a/b = 2, δ = π/2). Otros valores de esta relación producen curvas más complicadas, las cuales sólo son cerradas si  es un número racional, esto es, si
es un número racional, esto es, si  y
y  son conmensurables. En el caso de que el cociente de frecuencia no sea un racional la curva además de no ser cerrada es un conjunto denso sobre un rectángulo, lo cual significa que la curva pasa arbitrariamente cerca de cualquier punto de dicho rectángulo.
son conmensurables. En el caso de que el cociente de frecuencia no sea un racional la curva además de no ser cerrada es un conjunto denso sobre un rectángulo, lo cual significa que la curva pasa arbitrariamente cerca de cualquier punto de dicho rectángulo.
 , esto es, la relación entre las frecuencias de los movimientos en x e y. Para un valor de 1, la figura es una elipse, con los casos especiales del círculo (A = B, δ = π/2 radianes) y de las rectas (δ = 0) incluidos. Otra de las figuras simples de Lissajous es la parábola (a/b = 2, δ = π/2). Otros valores de esta relación producen curvas más complicadas, las cuales sólo son cerradas si
, esto es, la relación entre las frecuencias de los movimientos en x e y. Para un valor de 1, la figura es una elipse, con los casos especiales del círculo (A = B, δ = π/2 radianes) y de las rectas (δ = 0) incluidos. Otra de las figuras simples de Lissajous es la parábola (a/b = 2, δ = π/2). Otros valores de esta relación producen curvas más complicadas, las cuales sólo son cerradas si  es un número racional, esto es, si
es un número racional, esto es, si  y
y  son conmensurables. En el caso de que el cociente de frecuencia no sea un racional la curva además de no ser cerrada es un conjunto denso sobre un rectángulo, lo cual significa que la curva pasa arbitrariamente cerca de cualquier punto de dicho rectángulo.
son conmensurables. En el caso de que el cociente de frecuencia no sea un racional la curva además de no ser cerrada es un conjunto denso sobre un rectángulo, lo cual significa que la curva pasa arbitrariamente cerca de cualquier punto de dicho rectángulo.
En el caso de que el cociente sí sea un número racional, entonces existirán dos números naturales, nx y ny, tales que
y, obviamente, el periodo del movimiento resultante es el valor de T
obtenido utilizando los valores más pequeños que satisfagan la relación (fracción irreducible).
La apariencia de estas curvas a menudo sugiere un nudo de tres dimensiones u otros tipos de nudos, incluyendo los conocidos como nudos de Lissajous, proyección en el plano de las figuras de Lissajous.
Uso en logotipos
Las figuras de Lissajous son usadas como logotipos. Ejemplos de estos logotipos son el de Australian Broadcasting Corporation (a = 1, b = 3, δ = π/2) y el del Lincoln Laboratory at MIT (a = 8, b = 6, δ = 0). Las curvas de Lissajous pueden ser trazadas mecánicamente por medio de un armonógrafo.
Espirógrafo
Es bastante parecido en aspecto a las curvas de Lissajous, pero con pequeñas diferencias en cuanto a las Matemáticas subyacentes.





















No hay comentarios:
Publicar un comentario