El Cuerno de Gabriel (también llamado Trompeta de Torricelli) es una figura geométrica ideada por Evangelista Torricelli que tiene la característica de poseer una superficie infinita pero unvolumen finito. Es la superficie de revolución que se obtiene al girar, alrededor del eje X, el gráfico de la función F(x)=1/x, con dominio x ≥ 1.
Historia
En el momento de su descubrimiento, fue considerado una paradoja. Esta paradoja aparente ha sido descrita de modo informal señalando que sería necesaria una cantidad infinita de pintura para cubrir la superficie exterior, mientras que sería posible rellenar toda la figura con una cantidad finita de pintura y así cubrir esa superficie.
La solución de la paradoja es que un área infinita requiere una cantidad infinita de pintura si la capa de pintura tiene un grosor constante. Esto no se cumple en el interior del cuerno, ya que la mayor parte de la longitud de la figura no es accesible a la pintura, especialmente cuando su diámetro es menor que el de una molécula de pintura. Si se considera una pintura sin grosor, sería necesaria una cantidad infinita de tiempo para que ésta llegase hasta el «final» del cuerno.
En otras palabras, llegaría un momento en el que el espesor de la trompeta sería más pequeño que una molécula de pintura con lo que, digamos, una gota de pintura cubriría el resto de la superficie de la trompeta (aunque fuera infinito). Así, que la superficie de la trompeta sea infinita no implicaría que la cantidad de pintura tenga que ser infinita.
Pero la paradoja también tiene solución incluso si suponemos una materia divisible indefinidamente (o sea, si no existiesen los átomos). Si el grosor de la capa de pintura es variable y disminuye indefinidamente (tendiendo a cero), la cantidad de pintura se calcularía por una integral impropia que podría ser convergente. En este caso, el espesor de la capa de pintura forzosamente debería ser igual o menor al valor de y, lo que hace que la integral impropia, en este caso, sea convergente, es decir, se necesita una cantidad finita de pintura.
Ecuación matemática
El cuerno de Gabriel se forma utilizando la gráfica de 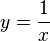 , con el dominio
, con el dominio  (al poseer la asíntota en
(al poseer la asíntota en  ), y rotándola en tres dimensiones alrededor del eje X. Su descubrimiento es anterior al cálculo y fue posible gracias al Principio de Cavalieri. Es posible calcular tanto el volumen
), y rotándola en tres dimensiones alrededor del eje X. Su descubrimiento es anterior al cálculo y fue posible gracias al Principio de Cavalieri. Es posible calcular tanto el volumen  como el área superficial
como el área superficial  del cuerno entre x = 1 y x = a, donde a > 1, mediante integración (véase sólido de revolución y superficie de revolución):
del cuerno entre x = 1 y x = a, donde a > 1, mediante integración (véase sólido de revolución y superficie de revolución):
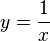 , con el dominio
, con el dominio  (al poseer la asíntota en
(al poseer la asíntota en  ), y rotándola en tres dimensiones alrededor del eje X. Su descubrimiento es anterior al cálculo y fue posible gracias al Principio de Cavalieri. Es posible calcular tanto el volumen
), y rotándola en tres dimensiones alrededor del eje X. Su descubrimiento es anterior al cálculo y fue posible gracias al Principio de Cavalieri. Es posible calcular tanto el volumen  como el área superficial
como el área superficial  del cuerno entre x = 1 y x = a, donde a > 1, mediante integración (véase sólido de revolución y superficie de revolución):
del cuerno entre x = 1 y x = a, donde a > 1, mediante integración (véase sólido de revolución y superficie de revolución): puede ser tan grande como se desee, pero en la ecuación se puede observar que el volumen del cuerno entre
puede ser tan grande como se desee, pero en la ecuación se puede observar que el volumen del cuerno entre 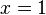 y
y  nunca será igual a
nunca será igual a  ; sin embargo, se acercará más y más a
; sin embargo, se acercará más y más a  conforme
conforme  crece. Matemáticamente, el volumen tiende a
crece. Matemáticamente, el volumen tiende a  conforme
conforme  tiende a infinito. Empleando límites, el volumen puede expresarse de la siguiente forma:
tiende a infinito. Empleando límites, el volumen puede expresarse de la siguiente forma:
Esto es así porque conforme  tiende a infinito,
tiende a infinito, 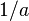 tiende a cero, lo cual implica que el volumen tienda a
tiende a cero, lo cual implica que el volumen tienda a  (1 - 0), que es igual a
(1 - 0), que es igual a  .
.
 tiende a infinito,
tiende a infinito, 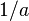 tiende a cero, lo cual implica que el volumen tienda a
tiende a cero, lo cual implica que el volumen tienda a  (1 - 0), que es igual a
(1 - 0), que es igual a  .
.
Con respecto al área, la fórmula anterior muestra que ésta es mayor que  veces el logaritmo neperiano de
veces el logaritmo neperiano de  . No existe una cota superior para el logaritmo neperiano de
. No existe una cota superior para el logaritmo neperiano de  conforme tiende a infinito, lo cual quiere decir que, en este límite, el cuerno tiene un área superficial infinita. Matemáticamente, esto es expresado de la siguiente forma:
conforme tiende a infinito, lo cual quiere decir que, en este límite, el cuerno tiene un área superficial infinita. Matemáticamente, esto es expresado de la siguiente forma:
 veces el logaritmo neperiano de
veces el logaritmo neperiano de  . No existe una cota superior para el logaritmo neperiano de
. No existe una cota superior para el logaritmo neperiano de  conforme tiende a infinito, lo cual quiere decir que, en este límite, el cuerno tiene un área superficial infinita. Matemáticamente, esto es expresado de la siguiente forma:
conforme tiende a infinito, lo cual quiere decir que, en este límite, el cuerno tiene un área superficial infinita. Matemáticamente, esto es expresado de la siguiente forma:
El Cuerno de Gabriel
El Cuerno de Gabriel (también llamado Trompeta de Torricelli) es una figura geométrica ideada por Evangelista Torricelli que tiene la característica de poseer una superficie infinita pero un volumen finito.Se define como la superficie de revolución que se obtiene al girar, alrededor del eje , el gráfico de la función para .En el momento de su descubrimiento fue considerado una paradoja. Esta paradoja aparente ha sido descrita de modo informal señalando que sería necesaria una cantidad infinita de pintura para cubrir la superficie interior, mientras sería posible rellenar toda la figura con una cantidad finita de pintura y así cubrir esa superficie.La solución de la paradoja es que un área infinita requiera una cantidad infinita de pintura si la capa de pintura tiene un grosor constante. Esto no se cumple en el interior del cuerno, ya que la mayor parte de la longitud de la figura no es accesible a la pintura, especialmente cuando su diámetro es menor que el de una molécula de pintura. Si se considera pintura sin grosor, sería necesaria una cantidad infinita de tiempo para que ésta llegase hasta el "final" del cuerno.En otras palabras, llegaría un momento en el que el espesor de la trompeta sería más pequeño que una molécula de pintura con lo que, digamos, una gota de pintura cubriría el resto de la superficie de la trompeta (aunque fuera infinito). Por tanto, el hecho de que la superficie de la trompeta sea infinita no implicaría que la cantidad de pintura tenga que ser infinita.Pero la paradoja también tiene solución incluso si suponemos una materia divisible indefinidamente (o sea, si no existiesen los átomos). Si el grosor de la capa de pintura es variable y disminuye indefinidamente (tendiendo a cero), la cantidad de pintura se calcularía por una integral impropia que podría ser convergente.En este caso, el espesor de la capa de pintura forzosamente debería ser igual o menor al valor de , lo que hace que la integral impropia, en este caso, sea convergente, es decir, se necesita una cantidad finita de pintura.Regresando al cálculo integral, tenemos que por el método de los discos:
Haciendo tender a infinito se tiene:
Por tanto, el volumen es igual a . Ahora toca reflexionar acerca del significado de .- curvas de Bézier a un sistema que se desarrolló hacia los años 1960 para el trazado de dibujos técnicos, en el diseño aeronáutico y en el de automóviles. Su denominación es en honor a Pierre Bézier, quien ideó un método de descripción matemática de las curvas que se comenzó a utilizar con éxito en los programas de CAD.Las curvas de Bézier fueron publicadas por primera vez en 1962 por el ingeniero francés Pierre Bézier, que las usó posteriormente con profusión en el diseño de las diferentes partes de los cuerpos de un automóvil, en sus años de trabajo en laRenault. Las curvas fueron desarrolladas por Paul de Casteljau usando el algoritmo que lleva su nombre. Se trata de un método numéricamente estable para evaluar las curvas de Bézier.Posteriormente, los inventores del PostScript, lenguaje que permitió el desarrollo de sistemas de impresión de alta calidad desde el ordenador, introdujeron en ese código el método de Bézier para la generación del código de las curvas y los trazados. El lenguaje PostScript sigue empleándose ampliamente y se ha convertido en un estándar de calidad universal; por ello, los programas de diseño vectorial como Adobe Illustrator, el extinto Macromedia FreeHand y Corel Draw, tres de los programas más importantes de dibujo vectorial y otros como Inkscape, denominan «bézier» a algunas de sus herramientas de dibujo, y se habla de «trazados bézier», «pluma bézier», «lápiz bézier», etc. Su facilidad de uso la ha estandarizado en el diseño gráfico, extendiéndose también a programas de animación vectorial, como Adobe Flash, y retoque fotográfico (bitmap), como Photoshop y Gimp, donde se usa para crear formas cerradas o selecciones.La idea de definir geométricamente las formas no es demasiado compleja: un punto del plano puede definirse por coordenadas. Por ejemplo, un punto A tiene unas coordenadas (x1, y1) y a un punto B le corresponde (x2,y2). Para trazar una recta entre ambos basta con conocer su posición.Si en lugar de unir dos puntos con una recta se unen con una curva, surgen los elementos esenciales de una curva Bézier; los puntos se denominan «puntos de anclaje» o «nodos». La forma de la curva se define por unos puntos invisibles en el dibujo, denominados «puntos de control», «manejadores» o «manecillas».
Examen de los casos
Curvas lineales de Bézier
Dados los puntos P0 y P1, una curva lineal de Bézier es una línea recta entre los dos puntos. La curva viene dada por la expresión:Curvas cuadráticas de Bézier
Una curva cuadrática de Bézier es el camino trazado por la función B(t), dados los puntos: P0, P1, y P2,Las fuentes de letras TrueType usan curvas de Bézier desdobladas compuestas por curvas cuadráticas de Bézier.Curvas cúbicas de Bézier
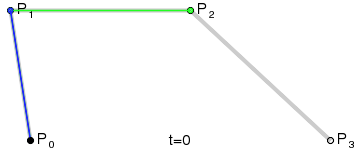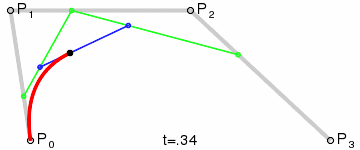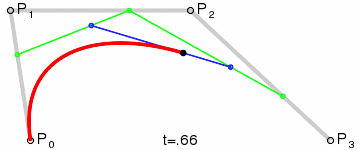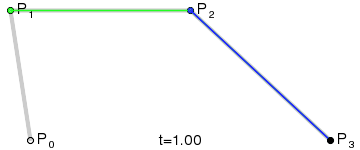
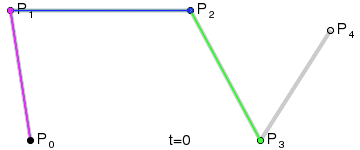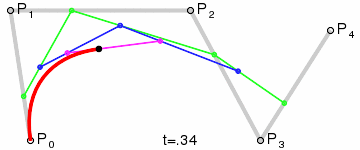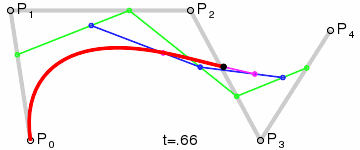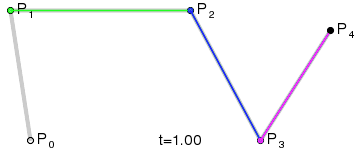
Cuatro puntos del plano o del espacio tridimensional, P0, P1, P2 y P3 definen una curva cúbica de Bézier. La curva comienza en el punto P0 y se dirige hacia P1 y llega a P3 viniendo de la dirección del punto P2. Usualmente, no pasará ni por P1 ni por P2. Estos puntos sólo están ahí para proporcionar información direccional. La distancia entreP0 y P1 determina "qué longitud" tiene la curva cuando se mueve hacia la dirección de P2 antes de dirigirse haciaP3.La forma paramétrica de la curva es:Los modernos sistemas de imágenes como PostScript, Asymptote y Metafont usan curvas de Bézier desdobladas, compuestas por curvas cúbicas de Bézier para dibujar las formas de las curvas.Generalización
La curva de Bézier de grado puede ser generalizada de la siguiente manera. Dados los puntos P0, P1,..., Pn, la curva de Bézier es del tipo:Por ejemplo, una curva de orden cinco (
puede ser generalizada de la siguiente manera. Dados los puntos P0, P1,..., Pn, la curva de Bézier es del tipo:Por ejemplo, una curva de orden cinco ( ) quedaría como:Esta ecuación puede ser expresada de manera recursiva como sigue: sea la expresión
) quedaría como:Esta ecuación puede ser expresada de manera recursiva como sigue: sea la expresión que denota la curva de Bézier determinada por los puntos P0, P1,...,Pn. EntoncesEn otras palabras, el grado
que denota la curva de Bézier determinada por los puntos P0, P1,...,Pn. EntoncesEn otras palabras, el grado de la curva de Bézier es una interpolación entre los dos grados
de la curva de Bézier es una interpolación entre los dos grados  de las curvas de Bézier.
de las curvas de Bézier.Terminología
Existe una terminología asociada exclusivamente para este tipo de curvas. Se tiene:donde las polinomialesson conocidas como polinomios de Bernstein de grado n, definidos por 00 = 1.Los puntos Pi son llamados puntos de control de las curvas de Bézier. El polígono formado por la conexión de los puntos de Bézier con rectas, comenzando por P0 y terminando en Pn, se denomina polígono de Bézier (o polígono de control). La envolvente convexa del polígono de Bézier contiene las curvas de Bézier.Notas
- La curva de Bézier se encuentra en el interior de la envolvente convexa de los puntos de control.
- La curva de Bézier es infinitamente derivable.
- El control de la curva es global. Modificar un punto de control implica modificar completamente la curva.
- Para efectuar una transformación afín de la curva es suficiente efectuar la transformación sobre todos los puntos de control.
- La curva comienza en el punto P0 y termina en el Pn. Esta peculiaridad es llamada interpolación del punto final.
- La curva es un segmento recto si, y sólo si, todos los puntos de control están alineados.
- El comienzo (final) de la curva es tangente a la primera (última) sección del polígono de Bézier.
- Una curva puede ser desdoblada en algunos puntos en dos curvas, o de manera arbitraria en tantas curvas como se quieran, cada una de las cuales es una nueva curva de Bézier.
- Algunas curvas que parecen simples, tales como una circunferencia, no pueden ser descritas de manera exacta mediante curvas de Bézier o segmentos de esta clase de curvas (por raro que parezca una curva formada a su vez por cuatro segmentos de curva puede aproximarse a un círculo, con un error radial máximo menor de una parte por mil, en cada punto de control interno la distancia es
 de manera horizontal o vertical de un punto de control del exterior sobre el círculo unidad).
de manera horizontal o vertical de un punto de control del exterior sobre el círculo unidad). - La curva compensada obtenida a partir de una curva de Bézier dada, frecuentemente llamada curva compensada (falsa "paralela" a la curva original, como los raíles en una vía de tren) no puede ser trazada de manera exacta mediante curvas de Bézier. De todas formas hay métodos heurísticos que proporcionan, normalmente, una aproximación adecuada en algunos propósitos prácticos.
Construcción de curvas de Bézier
Curvas lineales
La en la función para la curva lineal de Bézier se puede considerar como un descriptor de cuán lejos está
en la función para la curva lineal de Bézier se puede considerar como un descriptor de cuán lejos está  de
de 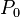 a
a  . Por ejemplo cuando
. Por ejemplo cuando  ,
,  es un cuarto de la longitud entre el punto
es un cuarto de la longitud entre el punto 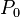 y el punto
y el punto  . Como
. Como  varía entre 0 y 1,
varía entre 0 y 1,  describe un línea recta de
describe un línea recta de 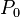 a
a 
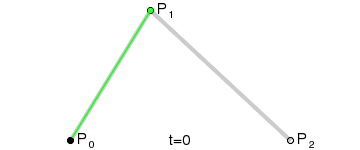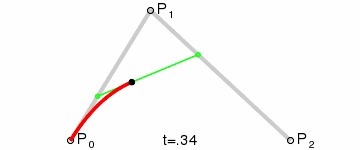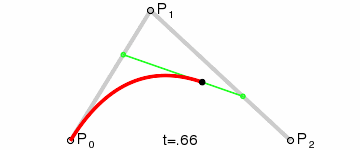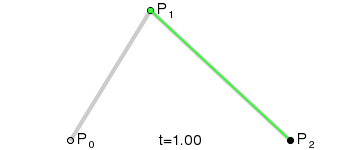
Curvas cuadráticas
Para curvas cuadráticas se pueden construir puntos intermedios desde a
a  tales que
tales que  varía de 0 a 1:
varía de 0 a 1:- Punto
 varía de
varía de 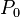 a
a  y describe una curva lineal de Bézier.
y describe una curva lineal de Bézier. - Punto
 varía de
varía de  a
a  y describe una curva lineal de Bézier.
y describe una curva lineal de Bézier. - Punto
 varía de
varía de  a
a  y describe una curva cuadrática de Bézier.
y describe una curva cuadrática de Bézier.
Curvas de órdenes superiores
Para curvas de orden superior se necesitan, lógicamente, más puntos intermedios. Para curvas cúbicas se pueden localizar puntos intermedios Q0, Q1 y Q2 que describen las curvas lineales de Bézier y los puntos R0 y R1 que describen las curvas cuadráticas:Y para curvas de grado 4, se pueden localizar los puntos intermedios Q0, Q1, Q2 y Q3 que describen las curvas lineales de Bézier, los puntos R0, R1 y R2 que describen las curvas cuadráticas y los puntos S0 y S1 que describen las curvas cúbicas.Aplicaciones
Gráficos de ordenador
Las curvas de Bézier han sido ampliamente usadas en los gráficos generados por ordenador para modelado de curvas suaves. Como la curva está completamente contenida en la envolvente convexa de los puntos de control, dichos puntos pueden ser visualizados gráficamente sobre el área de trabajo y usados para manipular la curva de una forma muy intuitiva. Las transformaciones afines tales como traslaciones y rotaciones pueden ser aplicadas, con gran facilidad, a las curvas, aplicando las transformaciones respectivas sobre los puntos de control.Las curvas cuadráticas y cúbicas son muy corrientes. Las curvas de grados superiores son más difíciles de evaluar. Cuanto más complejas son las superficies que se necesitan, las curvas de bajo orden son menos apropiadas. Para garantizar la suavidad de las curvas el punto de control en el que se juntan dos curvas y el punto de control sobre cualquiera de los lados debe ser colineal. Esta opción está frecuentemente desactivada en programas como Adobe Illustrator o Inkscape. Estas curvas poli-Bézier pueden ser observadas en el formato de archivo SVG.El método más simple para rasterizar una curva de Bézier es evaluarla en muchos puntos espaciados, muy próximos entre sí, y escanearla aproximando la secuencia de segmentos lineales.Esta manera de proceder no garantiza un resultado con la suficiente suavidad porque los puntos pueden estar espaciados demasiado separados. A la inversa, se pueden generar bastantes puntos de control en áreas donde la curva está cercana a la forma lineal.Un método adoptado, muy común, es la subdivisión recursiva, en el que los puntos de control de la curva son ajustados para ver si la curva se aproxima a segmentos lineales sin pequeñas tolerancias. Si esto no se logra, la curva es subdividida paramétricamente en dos segmentos y
y  y el mismo procedimiento se aplica por recursividad a cada mitad.También hay métodos que usan la diferenciación, pero se debe tener cuidado y analizar los errores de propagación. Los métodos analíticos donde un desdoble es intersecado con cada línea escaneada hallando raíces de polinomios de grado tres (por segmentación cúbica) y con múltiples raíces, pero no son frecuentes en la práctica.
y el mismo procedimiento se aplica por recursividad a cada mitad.También hay métodos que usan la diferenciación, pero se debe tener cuidado y analizar los errores de propagación. Los métodos analíticos donde un desdoble es intersecado con cada línea escaneada hallando raíces de polinomios de grado tres (por segmentación cúbica) y con múltiples raíces, pero no son frecuentes en la práctica.Síntesis de sonido
La síntesis de Bézier es un nuevo método de síntesis de ondas sonoras que se puede usar para crear sonidos usando curvas de Bézier.Ejemplo de código
El código que se lista a continuación es un ejemplo práctico que muestra como se traza una curva cúbica de Bézier en un programa usando lenguaje de programación C. Nótese que este simplemente calcula los coeficientes de un polinomio y se ejecuta a través de una serie de valores de comprendidos en el intervalo
comprendidos en el intervalo ![[0,1]](https://upload.wikimedia.org/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) . En la práctica no es como se procede de manera normal. Con frecuencia, una solución recursiva es más rápida, consumiendo menos ciclos de procesador y a expensas de requerir más memoria para el cálculo, de manera temporal. Incluso el método directo ilustrado aquí es más fácil de comprender y produce el mismo resultado. El siguiente código ha sido compilado para hacer esta operación más clara. En la práctica una optimización podría ser calcular los coeficientes una vez y posteriormente usar los resultados para reprocesarlos y calcular los puntos de la curva. Aquí son recalculados cada vez, lo que es menos eficiente pero ayuda a clarificar el código.La curva resultante puede ser trazada dibujando líneas entre puntos sucesivos en la matriz de la curva. A más puntos más suavidad en la silueta de la curva.En algunas arquitecturas, el código de abajo puede ser optimizado también por programación dinámica. Por ejemplo donde
. En la práctica no es como se procede de manera normal. Con frecuencia, una solución recursiva es más rápida, consumiendo menos ciclos de procesador y a expensas de requerir más memoria para el cálculo, de manera temporal. Incluso el método directo ilustrado aquí es más fácil de comprender y produce el mismo resultado. El siguiente código ha sido compilado para hacer esta operación más clara. En la práctica una optimización podría ser calcular los coeficientes una vez y posteriormente usar los resultados para reprocesarlos y calcular los puntos de la curva. Aquí son recalculados cada vez, lo que es menos eficiente pero ayuda a clarificar el código.La curva resultante puede ser trazada dibujando líneas entre puntos sucesivos en la matriz de la curva. A más puntos más suavidad en la silueta de la curva.En algunas arquitecturas, el código de abajo puede ser optimizado también por programación dinámica. Por ejemplo donde es constante,
es constante,  cambia una cantidad constante con cada iteración. Por aplicación repetida, el bucle puede ser reescrito sin ninguna multiplicación, aunque tal procedimiento no es numéricamente estable.
cambia una cantidad constante con cada iteración. Por aplicación repetida, el bucle puede ser reescrito sin ninguna multiplicación, aunque tal procedimiento no es numéricamente estable./* Código para generar una curva cúbica de Bézier */ typedef struct { float x; float y; } Point2D; /* cp es una matriz de 4 elementos donde: cp[0] es el primer punto, o P0 en el diagrama de abajo cp[1] es el primer punto de control, o P1 en el diagrama de abajo cp[2] es el segundo punto de control, o P2 en el diagrama de abajo cp[3] es el punto final, o P3 en el diagrama de abajo t es el valor del parámetro, 0 <= t <= 1 */ Point2D PointOnCubicBezier( Point2D* cp, float t ) { float ax, bx, cx; float ay, by, cy; float tSquared, tCubed; Point2D result; /* cálculo de los coeficientes polinomiales */ cx = 3.0 * (cp[1].x - cp[0].x); bx = 3.0 * (cp[2].x - cp[1].x) - cx; ax = cp[3].x - cp[0].x - cx - bx; cy = 3.0 * (cp[1].y - cp[0].y); by = 3.0 * (cp[2].y - cp[1].y) - cy; ay = cp[3].y - cp[0].y - cy - by; /* calculate the curve point at parameter value t */ tSquared = t * t; tCubed = tSquared * t; result.x = (ax * tCubed) + (bx * tSquared) + (cx * t) + cp[0].x; result.y = (ay * tCubed) + (by * tSquared) + (cy * t) + cp[0].y; return result; } /* ComputeBezier fills an array of Point2D structs with the curve points generated from the control points cp. Caller must allocate sufficient memory for the result, which is
*/ void ComputeBezier( Point2D* cp, int numberOfPoints, Point2D* curve ) { float dt; int i; dt = 1.0 / ( numberOfPoints - 1 ); for( i = 0; i < numberOfPoints; i++) curve[i] = PointOnCubicBezier( cp, i*dt ); } Otra aplicación de las curvas de Bézier es la descripción de los pasos para el movimiento de objetos en animaciones, etc. Aquí la x y las posiciones de la curva no son usadas para trazar la curva pero sí la posición en la gráfica. Cuando se usa de este modo, la distancia entre puntos sucesivos puede llegar a ser muy importante y, en general, estos no están espaciados de manera ecuánime. Si se requiere una linealidad en el movimiento, para procesar el cálculo más rápido, incluso en contra del camino deseado es necesario desdoblar los puntos resultantes.Curvas racionales de Bézier
Este tipo de curvas ajustan automáticamente los coeficientes de las ecuaciones paramétricas para obtener una aproximación a una figura arbitraria. El numerador es una ponderación de una curva Bézier en su forma de Berstein y el denominador es una suma ponderada de polinomios de Berstein.Dados n + 1 puntos de control Pi, la curva racional puede ser descrita por:o simplemente:
- La curva de Gosper, nombrada así en honor a Bill Gosper, es una curva de Peano. Es un fractal similar en su construcción a la curva del dragón o a la de Hilbert.

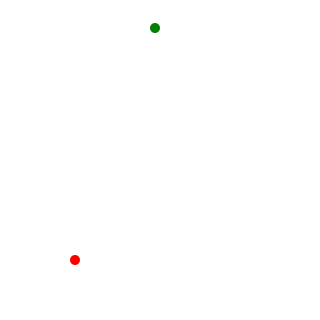
Cuarta iteración de la curva de Gosper. La línea que una el punto rojo con el verde muestra un solo paso de la construcción de la curva. Aquí se muestra un programa en Logo para dibujar la curva de Gosper mediante gráficos de tortuga:to rg :st :ln make "st :st - 1 make "ln :ln / 2.6457 if :st > 0 [rg :st :ln rt 60 gl :st :ln rt 120 gl :st :ln lt 60 rg :st :ln lt 120 rg :st :ln rg :st :ln lt 60 gl :st :ln rt 60] if :st = 0 [fd :ln rt 60 fd :ln rt 120 fd :ln lt 60 fd :ln lt 120 fd :ln fd :ln lt 60 fd :ln rt 60] end to gl :st :ln make "st :st - 1 make "ln :ln / 2.6457 if :st > 0 [lt 60 rg :st :ln rt 60 gl :st :ln gl :st :ln rt 120 gl :st :ln rt 60 rg :st :ln lt 120 rg :st :ln lt 60 gl :st :ln] if :st = 0 [lt 60 fd :ln rt 60 fd :ln fd :ln rt 120 fd :ln rt 60 fd :ln lt 120 fd :ln lt 60 fd :ln] endEl programa puede ser llamado, por ejemplo, conrg 4 300, o, alternativamentegl 4 300.La constante 2,6457 utilizada en el código del programa es una aproximación de √7.Propiedades
El espacio cubierto por la curva se denomina isla de Gosper. Aquí se muestran las primeras iteraciones de este fractal.



 La isla de Gosper puede cubrir completamente el plano. De hecho, se pueden unir entre sí siete copias de la isla de Gosper para formar una figura similar pero de tamaño √7 veces mayor en las dos dimensiones del plano. Iterando este proceso indefinidamente, se consigue una teselación del plano. De modo análogo, se puede extender la isla de Gosper a una curva infinita que cubra el plano.
La isla de Gosper puede cubrir completamente el plano. De hecho, se pueden unir entre sí siete copias de la isla de Gosper para formar una figura similar pero de tamaño √7 veces mayor en las dos dimensiones del plano. Iterando este proceso indefinidamente, se consigue una teselación del plano. De modo análogo, se puede extender la isla de Gosper a una curva infinita que cubra el plano.






![\mathbf{B}(t)=\mathbf{P}_0 + (\mathbf{P}_1-\mathbf{P}_0)t=(1-t)\mathbf{P}_0 + t\mathbf{P}_1 \mbox{ , } t \in [0,1].](https://upload.wikimedia.org/math/5/3/f/53f70cb65e4c07b3cc58d1d5ba76b72c.png)
![\mathbf{B}(t) = (1 - t)^{2}\mathbf{P}_0 + 2t(1 - t)\mathbf{P}_1 + t^{2}\mathbf{P}_2 \mbox{ , } t \in [0,1].](https://upload.wikimedia.org/math/b/0/a/b0a53071f8baba155c699a30f26f60b0.png)

![\mathbf{B}(t)=\mathbf{P}_0(1-t)^3+3\mathbf{P}_1t(1-t)^2+3\mathbf{P}_2t^2(1-t)+\mathbf{P}_3t^3 \mbox{ , } t \in [0,1].](https://upload.wikimedia.org/math/3/8/7/3870839539dcde1329de7b07b09bfff2.png)
![\mathbf{B}(t)=\sum_{i=0}^n {n\choose i}\mathbf{P}_i(1-t)^{n-i}t^i =\mathbf{P}_0(1-t)^n+{n\choose 1}\mathbf{P}_1(1-t)^{n-1}t+\cdots+\mathbf{P}_nt^n \mbox{ , } t \in [0,1].](https://upload.wikimedia.org/math/8/c/e/8ce08ca45bf146d5ec689f731367b326.png)
![\mathbf{B}(t)=\mathbf{P}_0(1-t)^5+5\mathbf{P}_1t(1-t)^4+10\mathbf{P}_2t^2(1-t)^3+10\mathbf{P}_3t^3(1-t)^2+5\mathbf{P}_4t^4(1-t)+\mathbf{P}_5t^5 \mbox{ , } t \in [0,1].](https://upload.wikimedia.org/math/4/f/0/4f06468b00fcd742c2e9ed1350190c19.png)
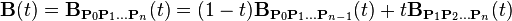
![\mathbf{B}(t) = \sum_{i=0}^n \mathbf{P}_i\mathbf{b}_{i,n}(t),\quad t\in[0,1]](https://upload.wikimedia.org/math/3/d/8/3d8f42d9608ecbd44e2f57758d159eb2.png)
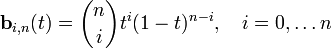


![t \in [0,1]](https://upload.wikimedia.org/math/d/9/a/d9a06fde4663cdd5b1ba693e9127232f.png) .
.


No hay comentarios:
Publicar un comentario