Campila de Eudoxo
La campila de Eudoxo (en griego καμπύλη: curva) es una curva determinada por una ecuación cartesiana:
de la cual se ha de excluir la solución x = y = 0, o, en coordenadas polares:
El astrónomo y matemático griego Eudoxo de Cnido (c. 408 a. C. - c. 347 a. C.) estudió esta curva cuártica en relación con el problema clásico de la duplicación del cubo.
La campila es simétrica con respecto a ambos ejes:  y
y  . Corta el eje
. Corta el eje  en
en  y en
y en  . Tiene cuatro puntos de inflexión, en:
. Tiene cuatro puntos de inflexión, en:
 y
y  . Corta el eje
. Corta el eje  en
en  y en
y en  . Tiene cuatro puntos de inflexión, en:
. Tiene cuatro puntos de inflexión, en:
(uno en cada cuadrante). La primera mitad de la curva es asintótica a  cuando
cuando  . En efecto se puede escribir así:
. En efecto se puede escribir así:
 cuando
cuando  . En efecto se puede escribir así:
. En efecto se puede escribir así:
donde
es el  ésimo número de Catalan.
ésimo número de Catalan.
 ésimo número de Catalan.
ésimo número de Catalan.Caracol de Pascal
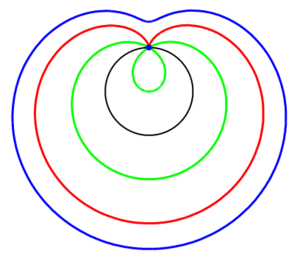
El caracol o "limaçon" de Pascal es la concoide de una circunferencia que pase por el polo. Es un tipo de epitrocoide.
Por tanto, su ecuación en coordenadas polares es:
En el caso particular de h=2·a, se obtiene una cardioide:

- Caracol de Pascal
Se puede definir como el lugar geométrico de los puntos del plano cuya distancia a los puntos de una circunferencia es una constante, estando la distancia medida en las cuerdas trazadas desde un punto fijo de la propia circunferencia.Al trazar una cuerda con origen en el punto A de una circunferencia, la cortará en otro punto que representaremos por M. Los puntos P y Q de la semirrecta AM que cumplen la condición PM = QM = b pertenecen al caracol de Pascal, siendo b la constante.La expresión en coordenadas cartesianas de esta curva es:siendo "a" el radio de la circunferencia y "b" la constante que determina la distancia de los puntos.
En coordenadas polares el caracol se expresa por la igualdad:Las expresiones anteriores determinan una familia de curvas, ya que según la relación existente entre los valores a y b obtendremos distintas curvas, algunas con denominación propia.Así cuando b = 2 a , aparece una cardioide y para b = a se obtiene la curva denominada trisectriz.Un procedimiento para obtener esta curva consiste en fijar un punto A en el plano y un punto M en una circunferencia, trazar la circunferencia con centro en M y radio AM y construir el lugar geométrico descrito por esta circunferencia cuando M recorre la circunferencia inicial.Cambiando la posición del punto A, observaremos los efectos que produce en el lugar geométrico, obteniendo como caso particular la cardioide cuando el punto A está en la circunferencia.El caracol de Pascal también se puede obtener como la curva podaria de una circunferencia con respecto a un punto del plano.Partiendo de una situación análoga a la anterior, un punto M de una circunferencia y un punto exterior A, trazamos la perpendicular por el punto A a la recta tangente a la circunferencia en el punto M. El punto P, intersección de las dos rectas, es un punto de la curva que se completará al mover el punto M en la circunferencia.Evidentemente, cuando el punto A también es de la circunferencia, aparecerá la cardioide. - círculo de Ford es un círculo centrado en
 y con radio
y con radio  , donde
, donde  es una fracción irreducible, es decir, p y q son números enteros primos entre sí.
es una fracción irreducible, es decir, p y q son números enteros primos entre sí. -
Círculos de Ford. Cada uno de estos círculos se apoya sobre un número racional - una fracción. Los círculos oscuros corresponden a las fracciones 0/1, 1/1, 1/2, 1/3, 2/3, 1/4, 3/4, 1/5, 2/5, 3/5 y 4/5. Cada círculo estangente a la recta real y a los círculos vecinos. Las fracciones irreducibles con el mismo denominador tendrán círculos del mismo tamaño.
Historia
Los círculos de Ford reciben el nombre del matemático estadounidense Lester R. Ford, Sr., quien los describió en un artículo en American Mathematical Monthly en1938, volumen 45, número 9, páginas 586-601.Propiedades
El círculo de Ford asociado a la fracción p/q se denota como C[p/q] o C[p, q]. Existe un círculo de Ford asociado a cualquier número racional. Es más, se puede considerar que la recta y = 1 es un círculo de Ford, concretamente el asociado con el infinito, el caso en que p = 1 y q = 0.Dos círculos de Ford distintos son, o bien disjuntos o bien tangentes entre sí, pero el interior de un círculo de Ford no puede intersecar con el interior de otro círculo de Ford a pesar de que haya un círculo de Ford tangente al eje horizontal en cada uno de sus puntos de coordenada racional. Si p/q está entre 0 y 1, los círculos de Ford que son tangentes a C[p/q] son precisamente aquellos que están asociados con las fracciones que son la anterior o posterior a p/q en una sucesión de Farey determinada.También se puede pensar en los círculos de Ford como curvas en el plano complejo. El grupo modular Gamma de transformaciones del plano complejo lleva círculos de Ford a otros círculos de Ford.Interpretando la mitad superior del plano complejo como un modelo del plano hiperbólico (el modelo de semiplano de Poincaré), los círculos de Ford también se pueden interpretar como una teselación del plano hiperbólico mediante horociclos. Dos círculos de Ford cualesquiera son congruentes en la geometría hiperbólica. Si C[p/q] y C[r/s] son círculos de Ford tangentes entre sí, entonces el semicírculo que une (p/q, 0) con (r/s, 0) que es perpendicular con el eje x es una recta hiperbólica que también pasa por el punto donde los dos círculos son tangentes entre sí.Los círculos de Ford son un subconjunto de los círculos presentes en el círculo de Apolonio generado por las rectas y = 0 e y = 1 y el círculo C[0/1].Área total de los círculos de Ford
Existe una relación entre el área total de los círculos de Ford, la función φ de Euler y la función zeta de Riemann.Como ningún círculo de Ford interseca a ningún otro, se sigue inmediatamente que el área total de los círculos de Ford,![\left\{ C[p,q]: 0 \le \frac{p}{q} < 1 \right\}](https://upload.wikimedia.org/math/3/c/5/3c59f94359c009b0582ca5a0c8e5cfb2.png) ,
,
es menor que 1. De hecho, el área total se puede expresar por una suma convergente que puede ser evaluada.Aplicando la definición, el área es igual a:Al simplificar esta expresión, se obtiene:donde la última igualdad refleja la función generatriz de Dirichlet de φ(q). Como ζ(4) = π 4/90, se obtiene:Esta suma fue comentada en el grupo de noticias es.ciencia.matematicas.- En matemáticas, un círculo de Ford es un círculo centrado en
 y con radio
y con radio  , donde
, donde  es una fracción irreducible, es decir, p y q son números enteros primos entre sí. El círculo de Ford asociado a la fracción p/q se denota como C[p/q] ¿Qué tienen estos círculos de particular? Si los representamos nos daremos cuenta de ello:
es una fracción irreducible, es decir, p y q son números enteros primos entre sí. El círculo de Ford asociado a la fracción p/q se denota como C[p/q] ¿Qué tienen estos círculos de particular? Si los representamos nos daremos cuenta de ello: Efectivamente: dos círculos de Ford son, o bien disjuntos o bien tangentes entre sí. Curioso, ¿no?Los círculos de Ford reciben el nombre del matemático estadounidense Lester R. Ford, quien los describió en un artículo en American Mathematical Monthlyen 1938. Algunas propiedades de estos círculos son:
Efectivamente: dos círculos de Ford son, o bien disjuntos o bien tangentes entre sí. Curioso, ¿no?Los círculos de Ford reciben el nombre del matemático estadounidense Lester R. Ford, quien los describió en un artículo en American Mathematical Monthlyen 1938. Algunas propiedades de estos círculos son:- Si 0<p/q<1 a="" c="" de="" entonces="" ford="" i="" los="" que="" rculos="" son="" style="font-family: Baskerville, 'Times New Roman', Times, serif; font-size: 1.2em; font-stretch: normal; letter-spacing: 0.02em; line-height: normal; margin: 0px; padding: 0px;" tangentes="">p/q

Los círculos de Ford pueden servir para crear arte y si no véanse los resultados del artista Jos Leys.








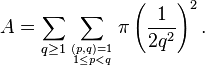
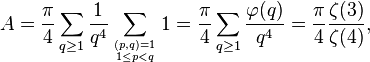




No hay comentarios:
Publicar un comentario