miércoles, 3 de febrero de 2016

Figuras geométricas epónimos


Concoide de Nicomedes

Conchoid of Nicomedes.png
La concoide de Nicomedes es la concoide de la recta, llamada "base".
Se pondrá la base perpendicular al eje polar, a una distancia b del polo y el radio de la circunferencia será h. Entonces, la ecuación de la concoide de Nicomedes es
\rho=\frac{b}{cos\ \omega} + h
que, en coordenadas cartesianas, queda:
(x-b)^2(x^2+y^2)=h^2 x^2 \,



Nicomedes nació sobre el año 280 a.C. en Grecia. Murió: sobre el año 210 a.C.
Se sabe muy poco de la vida de Nicomedes, incluso para establecer el periodo en el que vivió hay que hacerlo con referencias indirectas. Se sabe que Nicomedes criticó la duplicación del cubo de Eratóstenes (276 a. C.-194 a. C.) y que Apolonio (262 a.C.-190 a.C.) también habló de Nicomedes, así con estos datos apócrifos se estable el periodo en el que vivió.
Es famoso por su tratado "Las líneas de la concoide", y quiso utilizar la concoide para intentar solucionar los problemas clásicos de la trisección del ángulo y la duplicación del cubo.
I.- Concoide de Nicomedes.
Para dibujar la Concoide de Nicomedes necesitamos los siguientes elementos:
  1. Dibujamos una recta r (la directriz).
  2. Un punto exterior a la recta O (origen o polo).
  3. Un segmento con una longitud determinada k (constante).
Y procedemos de la siguiente manera:
  1. Desde O se traza una recta cualquiera s que corta a r ( la directriz) en el punto P.
  2. Con centro en P y radio k se traza una circunferencia que corta a la recta s en los punto Q1 y Q2, es decir Q1 y Q2 verifican d(Q1,P)=k;   d(Q2,P)=k.
El lugar geométrico de los puntos Q1 y Q2 cuando P recorre la recta r es la concoide de r con respecto al polo O y constante k.
Su fórmula implícita es la siguiente, donde la directriz es y=b y la constante (radio de la circunferencia es r=k): 
Para comprender mejor las explicaciones anteriores, ayúdate de la siguiente escena, cambiando los valore de k, de b y sobre todo moviendo el punto P sobre la recta directriz. NO olvides que la concoide de Nicomedes, es un lugar geométrico.
II.- La Concoide de Nicomedes como Trisectriz.
a) Ángulos en un rectángulo.
Ante de hablar de la concoide de Nicomedes como trisectriz, nos tenemos que convencer, o mas bien recordar, la relación de ángulos que hay en un rectángulo, para ello tenemos la siguiente escena. Los mismos colores, indican ángulos iguales.
  • Nombra, todos los triángulos rectángulos que hay en la escena.
  • Nombra todos los triángulos isósceles que hay en la escena, indicando cuales son los lados iguales.
Dar una explicación razonada para justificar la igualdades de los ángulos que tienen el mismo color.
Convéncete de los resultados de la escena modificándola, para ello puedes usar los controles disponibles.
b) Trisección de un ángulo agudo usando la Concoide de Nicomedes.
Veamos como se puede obtener la trisección de un ángulo agudo, usando la concoide de Nicomedes.
NOTACIÓN: Entenderemos por ángulo(AOB)  al ángulo mas pequeño que se puede definir con los vértices A, O y B siendo O el vértice.
Primero vamos a entender como se ha hecho el dibujo y en que orden:
  1. Trazamos un ángulo agudo, en  nuestro caso el ángulo(AOB).
  2. Trazamos una recta perpendicular al lado AO. Esta recta cortará a lado AO en A y al lado OB en B.
  3. Construimos la Concoide de Nicomedes con los siguientes elementos:
    •  Como Polo el punto  O.
    •  Como constante la distancia de O a B, es decir k=dist(O,B).
    •  Usaremos como directriz, la recta que trazamos perpendicular al lado AO
  4. Trazamos una recta perpendicular a la directriz que pase por B, y que cortará a la concoide de Nicomedes en el punto Q.
  5. Como se puede comprobar en la escena (recuerda, comprobar no es demostrar), el ángulo(AOQ) es la tercera parte del ángulo(AOB).

  • Antes de analizar la demostración siguiente, manipula la siguiente escena, cambiando el valor del ángulo, y sin perder de vista al puntoQ, observa como siempre está sobre l a Concoide.
  • Observa también, como automáticamente la escena dibuja siempre la Concoide con la constantek=2*dist(O,B) pues de no ser así, el resultado no sería válido

 c) Demostración de la exactitud del resultado.
Para demostrar el resultado anterior, lo haremos paso a paso:
  1. El punto Q es un punto de la Concoide, y por lo tanto dist(N,Q)=2*dist(O,B)=2*dist(N,M)=2*dist(M,Q)=k, y para garantizarlo observemos lo siguiente: Oestá en la recta que une N y Q, la propia definición de la Concoide y que M es el punto medio entre N y Q.
  2. El ángulo(AOQ)=ángulo(OQB) pues son ángulos que se forman al cortar dos recta paralelas, con la recta que contiene al segmento OQ.
  3. Como no hay ningún problema en considerar dibujado el rectángulo de vértices ABQP, como se muestra en la escena, podemos afirmar que el ángulo(NMB)=2*ángulo(OQB).
  4. Se observa que el  triángulo OMB es isósceles pues los lados MB y OB son iguales, como queda de manifiesto en el punto número 1 de este apartado, y en consecuencia tenemos la siguiente igualdad,  ángulo(NMB)=ángulo(OMB)=ángulo(MOB)
  5. Y por último uniendo los punto 2 y 3 tenemos las siguientes igualdades:
ángulo(NMB)=ángulo(MOB)=2*ángulo(OQB)=2*ángulo(AOQ) que demostraría lo que queríamos.
III.- Ejercicios.
 1.- En la escena siguiente, se puede:
  1. Mover el punto B arrastrándolo, o cambiando los valores de los controles B.x  y B.y (coordenadas de B)
  2. Mover el punto Q arrastrándolo.
  3. Cambiar el valor de la directriz (b) usando su correspondiente control.
  4. Cambiar el valor de la constante k usando su correspondiente control.
Observa que para cada ángulo, hay una sola concoide de Nicomedes que permite localizar la tercera parte del ángulo.
Manipulando la escena anterior, completa la siguiente tabla: (Ajusta los parámetros de la escena y coloca el punto Q en la intersección de la recta vertical roja y la concoide, en ese momento se debe de obtener un ángulo que es la tercera parte de AOB ).
ÁnguloDirectriz (b)Constante (k) Módulo OB
45º 8 
60º 8 
20º 10 
30º4  
25º5  
65º  3
35º  4









conjuntos de Julia, así llamados por el matemático Gaston Julia, son una familia de conjuntos fractales que se obtienen al estudiar el comportamiento de los números complejos al ser iterados por una función holomorfa.
El conjunto de Julia de una función holomorfa f\, está constituido por aquellos puntos que bajo la iteración de f\, tienen un comportamiento 'caótico'. El conjunto se denota J(f)\,.
En el otro extremo se encuentra el conjunto de Fatou (en honor del matemático Pierre Fatou), que consiste de los puntos que tienen un comportamiento 'estable' al ser iterados. El conjunto de Fatou de una función holomorfa f\, se denota F(f)\, y es el complemento de J(f)\,.

Polinomios cuadráticos

Una familia muy notable de conjuntos de Julia se obtienen a partir de funciones cuadráticas simples: f_c(z) = z^2 + c\,, donde c\, es un número complejo. El conjunto de Julia que se obtiene a partir de esta función se denota J_c\,.
Un algoritmo para obtener el conjunto de Julia de f_c(z) = z^2 + c\, es el siguiente:
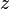Para todo complejo z\, se construye por la siguiente sucesión:
z_0 = z\,
z_{n+1} = z_n^2 + c
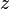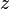Si esta sucesión queda acotada, entonces se dice que z\, pertenece al conjunto de Julia de parámetro c\,, denotado por J_c\,; de lo contrario, z\, queda excluido de éste.
En las imágenes anteriores, los puntos negros pertenecen al conjunto y los de color no. Los colores dan una indicación de la velocidad con la que diverge la sucesión (su módulo tiende a infinito): en rojo oscuro, al cabo de pocos cálculos se sabe que el punto no está en el conjunto; y en blanco, se ha tardado mucho más en comprobarlo. Como no se pueden calcular infinitos valores, es preciso poner un límite, y decidir que si los n\, primeros términos de la sucesión están acotados, el punto pertenece al conjunto. Al aumentar el valor de n\, se mejora la precisión de la imagen.
Conjunto de Julia en 3D.
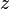Se puede demostrar que si |z_n| > 2\, entonces la sucesión diverge y el punto z no pertenece al conjunto de Julia. Por lo tanto, basta encontrar un solo término de la sucesión que verifique |z_n| > 2\, para tener la certeza de que z\, no está en el conjunto.
Existe una relación muy fuerte entre los conjuntos de Julia y el conjunto de Mandelbrot denotado por M\,, debido a la similitud de sus definiciones:
Se dice que c\, pertenece a M\, si y sólo si J_c\, es conexo.
Los resultados más vistosos se obtienen al tomar el parámetro c\, en la frontera de M\,, pues si c\, esta en el interior de M\, resulta que J_c\, toma el aspecto de un objeto redondo, poco fractal, y sólo el borde tiene la apariencia de fractal. Por ejemplo si c = 0resulta que el conjunto de Julia es la circunferencia unitaria, con centro en el origen de coordenadas.
En las imágenes, se han tomado como valores de c: -1,3 + 0,00525·i; -0,72 – 0,196·i; -0,1 + 0,87·i y -0,51 – 0,601·i, por razones estéticas.
Se pueden generalizar estos conjuntos tomando otras relaciones de inducción: z_{n+1} = f(z_n)\, con cualquier función compleja f\,. Se puede también generalizar a cualquier dimensión, y emplear varias funciones en lugar de una sola.

Ejemplos de Conjuntos de Julia

  • f(z) = z2 + 0.279
    •  
  • f(z) = z3 + 0.400
    •  
  • f(z) = z4 + 0.484
    •  
  • f(z) = z5 + 0.544
    •  
  • f(z) = z6 + 0.590
    •  
  • f(z) = z7 + 0.626
    •  
  • f(z) = exp(z) - 0.65
    •  
  • f(z) = exp(z3) - 0.59
    •  
  • f(z) = exp(z3) - 0.621
    Zoom x9
    •  
  • f(z) = z * exp(z) + 0.04
    •  
  • f(z) = z2 * exp(z) + 0.21
    •  
  • f(z) = z3 * exp(z) + 0.33
    •  
  • f(z) = z4 * exp(Z) + 0.41
    •  
  • f(z) = Sqr[Sinh(z2)] + (0.065,0.122i)
    •  
  • f(z) = [(z2+z)/Ln(z)] +(0.268,0.060i)
Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)