copo de nieve de Koch, también llamado estrella de Koch, es una curva cerrada continua pero no diferenciable en ningún punto descrita por el matemático sueco Helge von Koch en 1904 en un artículo titulado "Acerca de una curva continua que no posee tangentes y obtenida por los métodos de la geometría elemental".1 2
En lenguaje actual, diríamos que es una curva fractal. Su construcción más simple se realiza mediante un proceso iterativo que se inicia partiendo en tres un segmento de recta e insertando dos más en el tercero medio a manera de un triángulo equilátero, el proceso se repite infinidad de veces. La curva de Koch es un caso particular de curva de De Rham.
Construcción
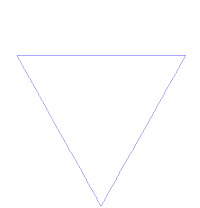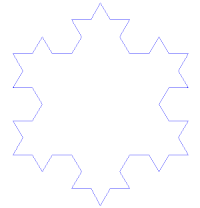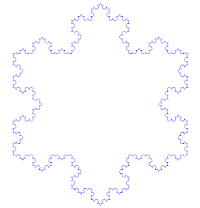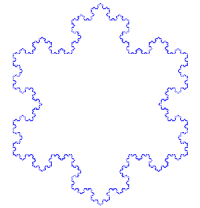
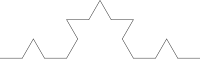
Veamos el proceso que lleva a sustituir cada lado por la llamada curva de Koch: Se toma un segmento, se lo divide en tres partes iguales, se remplaza la parte central por dos partes de igual longitud haciendo un ángulo de 60 grados. Luego, con los cuatro segmentos, se procede de la misma manera, lo que da lugar a 16 segmentos más pequeños en la segunda iteración. Y así sucesivamente. La figura representa las seis primeras etapas de la construcción. La última curva es una buena aproximación de la curva final.
Tres de estas curvas unidas forman el copo de nieve de Koch:
Representación como sistema Lindenmayer
La curva de Koch se puede expresar en el sistema Lindenmayer
Alfabeto : F Constantes : +, − Axioma : F++F++F Reglas de producción: F → F−F++F−F
Aquí, F significa «continua dibujando», + «gira 60 grados a la derecha, y - «gira 60 grados a la izquierda» (ver gráficas tortuga)
Propiedades
Longitud
Si se considera de nuevo la primera figura, notamos que para pasar de una línea a la siguiente se remplaza tres segmentos por cuatro de igual longitud, o sea que la longitud total es multiplicada por 4/3. Después de n pasos iterativos en la construcción recursiva la longitud de la curva es 3·(4/3)n, el límite de la sucesión geométricaanterior de razón 4/3 es obviamente infinito, lo que significa que la figura final tiene una longitud infinita (lo que Mandelbrot denomina infinito interno). Esto está relacionado con el hecho de que la curva frontera del copo de Koch no es rectificable y tiene una dimensión fractal d > 1.
Propiedades fractales
La característica anterior, típica de muchas curvas fractales, añadida al hecho que la curva da la impresión de tener cierto espesor a causa de sus constantes cambios de dirección, sugiere que esta figura, en algún sentido, no es unidimensional. Para ello usaremos una generalización del concepto de dimensión: la dimensión fractal de Hausdorff.
Su dimensión de Hausdorff tiene que estar entre 1, la de una recta, y 2, la del plano. Para hallarla miremos la última curva: Si agrandamos (mediante una homotecia) tres veces la sección A'B' obtenemos exactamente la sección AB. En la curva final, obtendríamos la sección A'C, es decir cuatro veces la sección inicial.
Se sabe que una homotecia de razón tres multiplica las longitudes por 3, las superficies por 3² = 9, los volúmenes por 3³ = 27, y más generalmente, el "volumen" de objeto de dimensión d por 3d. Entonces tenemos 3d = 4 para el copo de Koch, lo que da:
La dimensión de homotecia anterior coincide en este caso con la dimensión fractal de Hausdorff. La configuración opuesta-complementaria de un copo de nieve de Koch o copo de nieve fractal suele ser denominada anticopo de nieve.
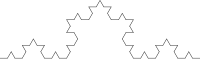
Partamos de un triángulo equilátero de lado unidad. Dividimos en tres partes iguales de longitud 1/3 cada lado. Sustituimos el segmento central por dos segmentos de tamaño idéntico formando un diente como muestra la animación en la iteración n=1. Tenemos una curva poligonal P1 de longitud 3·4··1/3=4. Repetimos la operación (n=2) con cada uno de los cuatro nuevos segmentos de cada uno de los "lados". Obtendremos así la curva P2 de longitud 3·42·1/32=16/3. La iteración indefinida nos proporciona la isla de Koch o copo de nieve de Koch.
En la operación n-ésima la curva estará formada por 3·4n trozos, de perímetro 4n /3n-1. La curva de Von Koch resulta del paso al límite de la sucesión de curvas Pn cuando n tiende a infinito. ¿Cuál es la longitud del perímetro de esta isla?
Será:
Será:
Es decir, aunque la isla de Von Koch ocupa una región limitada del espacio, un área finita, su perímetro es ... ¡infinito! @
Existen muchas variantes sobre la construcción de la curva de Kock @ @ . Abajo mostramos la curva de Koch exterior, que parte originalmente de un hexágono, en vez de un triángulo equilátero:
Abajo vemos dos versiones más que parten de un cuadrado. Se denominan fractales de Cesaro. Observemos que la variación del ángulo se traduce en dos resultados finales bien diferentes. @
Ya en la Grecia clásica existían varias definiciones para el concepto de curva. Desde las curvas entendidas como la intersección de superficies, caso de las cónicas, a la de curva entendida como el lugar geométrico de la trayectoria recorrida por un punto. En el siglo XVII la geometría analítica asocia curvas y ecuaciones algebraicas. Más tarde, el cálculo diferencial acaba reservando el nombre curva a la función continua.
Las curvas que estamos acostumbrados a tratar son "suaves". Imaginemos que trazamos una tangente a una de estas curvas en uno de sus puntos. Ampliemos una zona microscópica alrededor del punto de tangencia: a medida que nos acercamos más y más al entorno "infinitesimal" del punto, la línea tangente se ajusta más y más a la curva. Decimos que localmente la curva es indistinguible de una línea recta. De forma similar ocurre con una superficie: sobre cada punto podemos trazar un plano de tangencia. Decimos, entonces, que localmente la superficie es indistinguible de un plano.
La contrapartida algebraica es que podemos determinar analíticamente el valor de la derivada de la curva en el punto de tangencia. Si la curva representa la trayectoria de un móvil, el valor de la derivada en un punto nos proporciona su velocidad instantánea.
La contrapartida algebraica es que podemos determinar analíticamente el valor de la derivada de la curva en el punto de tangencia. Si la curva representa la trayectoria de un móvil, el valor de la derivada en un punto nos proporciona su velocidad instantánea.
Poliedro de Császár (ˈtʃaːsaːr) es un poliedro no convexo, topológicamente un toro, con 14 caras triangulares.
Este poliedro no tiene diagonales; cada par de vértices están conectados por una arista. Los 7 vértices y 21 aristas del poliedro forma el grafo completo  sobre la superficie de un toro.
sobre la superficie de un toro.
 sobre la superficie de un toro.
sobre la superficie de un toro.
El tetraedro y el poliedro de Császár son los únicos poliedros conocidos que no tienen diagonales, aunque hay otros poliedros conocidos tales como el poliedro de Schönhardt que no tienen diagonales interiores (es decir, todas las diagonales están en el exterior del poliedro), así como las superficies de una sola cara sin diagonales. Si un poliedro con v vértices es proyectado sobre una superficie con h agujeros, de alguna manera cada par de vértices se conecta por una arista, y se deduce de su característica de Euler que
Esta ecuación se satisface para el tetraedro con h = 0 y v = 4, y para el poliedro de Császar con h =1 y v =7. La próxima posible solución, h = 6 y v = 12, correspondería a un poliedro con 44 caras y 66 aristas, pero no es realizable como un poliedro; no se conoce si tal poliedro existe con un género mayor. De manera general, esta ecuación se puede satisfacer sólo cuando v es congruente con 0, 3, 4, ó 7 módulo 12.
El poliedro de Császár recibe su nombre por el topólogo Ákos Császár, quien lo descubrió en 1949. Su poliedro dual es el poliedro de Szilassi, que fue descubierto más tarde, en 1977, por Lajos Szilassi; éste tiene 14 vértices, 21 aristas, y 7 caras hexagonales, cada una comparte una arista con cada una de las otras caras. Al igual que el poliedro de Császár, el poliedro de Szilassi es topológicamente equivalente a un toro.
El poliedro de Császár
C + V = A +2
Para que esta relación sea cierta el poliedro ha de ser convexo, es decir, no tener huecos.
Pero hay un poliedro muy especial que tiene la misma propiedad que el tetraedro, esto es, cada vértice está unido con todos los demás mediante una arista y por tanto no tiene diagonales.
El poliedro de Császár tiene 7 vértices, 21 aristas y 14 caras triangulares.






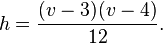
No hay comentarios:
Publicar un comentario