La banda o cinta de Möbius o Moebius (/ˈmøːbjʊs/) es una superficie con una sola cara y un solo borde. Tiene la propiedad matemática de ser un objeto no orientable. También es una superficie reglada. Fue descubierta en forma independiente por los matemáticos alemanes August Ferdinand Möbius y Johann Benedict Listing en1858.
Construcción de una cinta de Möbius
Para construir una cinta de Möbius, se toma una tira de papel y se pegan los extremos dando media vuelta a uno de ellos.
Propiedades
La banda de Möbius posee las siguientes propiedades:
- Es una superficie que sólo posee una cara:
Si se colorea la superficie de una cinta de Möbius, comenzando por la «aparentemente» cara exterior, al final queda coloreada toda la cinta, por tanto, sólo tiene una cara y no tiene sentido hablar de cara interior y cara exterior.
- Tiene sólo un borde:
Se puede comprobar siguiendo el borde con un dedo, apreciando que se alcanza el punto de partida tras haber recorrido la totalidad del borde.
- Es una superficie no orientable:
Si se parte con una pareja de ejes perpendiculares orientados, al desplazarse paralelamente a lo largo de la cinta, se llegará al punto de partida con la orientación invertida. Una persona que se deslizara «tumbada» sobre una banda de Möbius, mirando hacia la derecha, al recorrer una vuelta completa aparecerá mirando hacia la izquierda.
- Otras propiedades:
Si se corta una cinta de Möbius a lo largo, se obtienen dos resultados diferentes, según dónde se efectúe el corte.
Si el corte se realiza en la mitad exacta del ancho de la cinta, se obtiene una banda más larga pero con dos vueltas; y si a esta banda se la vuelve a cortar a lo largo por el centro de su ancho, se obtienen otras dos bandas entrelazadas. A medida que se van cortando a lo largo de cada una, se siguen obteniendo más bandas entrelazadas.1
Si el corte no se realiza en la mitad exacta del ancho de la cinta, sino a cualquier otra distancia fija del borde, se obtienen dos cintas entrelazadas diferentes: una de idéntica longitud a la original y otra con el doble de longitud.
Esta forma geométrica se utiliza frecuentemente como ejemplo en topología.
Geometría
Una forma de representar la banda de Möbius (cerrada y con frontera) como un subconjunto de  es mediante la parametrización:
es mediante la parametrización:
 es mediante la parametrización:
es mediante la parametrización:
donde  y
y  .
.
 y
y  .
.
Representa una banda doble de Möbius de ancho unitario, cuya circunferencia exterior tiene radio unitario y se encuentra en el plano coordenado x-y centrada en  . El parámetro u recorre la banda longitudinalmente, mientras v se desplaza de un punto a otro del borde, cruzando transversalmente la circunferencia central.
. El parámetro u recorre la banda longitudinalmente, mientras v se desplaza de un punto a otro del borde, cruzando transversalmente la circunferencia central.
 . El parámetro u recorre la banda longitudinalmente, mientras v se desplaza de un punto a otro del borde, cruzando transversalmente la circunferencia central.
. El parámetro u recorre la banda longitudinalmente, mientras v se desplaza de un punto a otro del borde, cruzando transversalmente la circunferencia central.
Con la parametrización anterior podemos obtener su curvatura gaussiana la cual es:
En coordenadas cilíndricas  , se puede representar una versión sin frontera (abierta) de la banda de Möbius mediante la ecuación:
, se puede representar una versión sin frontera (abierta) de la banda de Möbius mediante la ecuación:
 , se puede representar una versión sin frontera (abierta) de la banda de Möbius mediante la ecuación:
, se puede representar una versión sin frontera (abierta) de la banda de Möbius mediante la ecuación:Topología
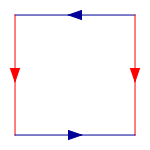
Topológicamente, la banda de Möbius puede definirse como el cuadrado ![\scriptstyle[0,1] \times [0,1]](https://upload.wikimedia.org/math/7/3/e/73e80ab91ce1e439d855abdc829e3c8e.png) que tiene sus aristas superior e inferior identificadas (topología cociente) por la relación
que tiene sus aristas superior e inferior identificadas (topología cociente) por la relación 
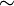
 para
para  , como en el diagrama que se muestra en la figura de la derecha.
, como en el diagrama que se muestra en la figura de la derecha.
![\scriptstyle[0,1] \times [0,1]](https://upload.wikimedia.org/math/7/3/e/73e80ab91ce1e439d855abdc829e3c8e.png) que tiene sus aristas superior e inferior identificadas (topología cociente) por la relación
que tiene sus aristas superior e inferior identificadas (topología cociente) por la relación 
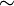
 para
para  , como en el diagrama que se muestra en la figura de la derecha.
, como en el diagrama que se muestra en la figura de la derecha.
La banda de Möbius es una variedad bidimensional (es decir, una superficie). Es un ejemplo estándar de una superficie noorientable. La banda de Möbius es un ejemplo elemental -también- para ilustrar el concepto matemático de fibrado topológico.
Como objeto topológico, la banda de Möbius también es considerada como el espacio total  de un fibrado no trivial teniendo como base el círculo
de un fibrado no trivial teniendo como base el círculo  y fibra un intervalo, i.e.
y fibra un intervalo, i.e.
 de un fibrado no trivial teniendo como base el círculo
de un fibrado no trivial teniendo como base el círculo  y fibra un intervalo, i.e.
y fibra un intervalo, i.e.
El contraste con el fibrado trivial  es agradable pues se sabe que sólo hay dos de estos fibrados E
es agradable pues se sabe que sólo hay dos de estos fibrados E
 es agradable pues se sabe que sólo hay dos de estos fibrados E
es agradable pues se sabe que sólo hay dos de estos fibrados EObjetos relacionados
Análoga a la banda de Möbius es la botella de Klein, pues también tiene sólo una superficie, donde no se puede diferenciar «fuera» de «dentro».
Esto último significa que mientras la banda se encaja (embedding) en  , la botella no.
, la botella no.
 , la botella no.
, la botella no.La banda de Möbius en el arte
Johann Sebastian Bach compuso un canon cuya partitura, al ejecutarse, guarda semejanza con la forma de una banda de Möbius.2
El artista M. C. Escher utilizó la banda de Möbius como motivo principal en diversas obras.3
El libro de cuentos Queremos tanto a Glenda, del escritor argentino Julio Cortázar, publicado en 1980, cuenta con una composición titulada Anillo de Moebius.4
El 17 de octubre de 1996, se estrenó la película Moebius,5 6 realizada en Argentina. Dicha película hace referencia a la teoría de la cinta que lleva el mismo nombre, aplicada a una supuesta red de subterráneos de la Ciudad de Buenos Aires ampliada. Se basa en un cuento de A. J. Deutsch, A Subway Named Moebius (1950).
Símbolos gráficos, logotipos y emblemas
El símbolo gráfico internacional de reciclaje y los de otras actividades similares, están basados en la imagen de la banda de Möbius.
Los partidos humanistas afiliados a la Internacional Humanista utilizan como logotipo un símbolo gráfico basado en la banda de Möbius.7
La Banda de Moebius
Uno de los objetos matemáticos más famosos dentro y fuera de la propia matemática
Una superficie ordinaria tiene dos caras. Esto se aplica a las superficies cerradas como la esfera y el toro, y a las superficies con contornos curvos, como un disco o un toro del que se haya quitado un trozo.
 Las dos caras de una superficie tal, podrían pintarse con colores diferentes para distinguirlas.
Las dos caras de una superficie tal, podrían pintarse con colores diferentes para distinguirlas.
Si la superficie es cerrada, los dos colores nunca se juntan.
Si la superficie tiene límites curvos, los dos colores se encuentran solamente a lo largo de estas curvas.
Un bicho que se arrastrara sobre tal superficie y tuviera prohibido cruzar las curvas límites, si existen, siempre quedaría en la misma cara.
A. F. Möbius hizo el sorprendente descubrimiento de que existen superficies con una sola cara.
La mas simple de estas superficies es la llamada banda de Möbius, formada tomando una larga tira rectangular de papel y uniendo sus extremos después de darle media vuelta.
Un bicho que se arrastrara sobre esta superficie, andando siempre por la parte media de la tira, llegaría a su posición original en el lado inferior, como se aprecia en el dibujo del artista gráfico M. C. Escher (1898-1972)
Uno de los objetos matemáticos más famosos dentro y fuera de la propia matemática
Una superficie ordinaria tiene dos caras. Esto se aplica a las superficies cerradas como la esfera y el toro, y a las superficies con contornos curvos, como un disco o un toro del que se haya quitado un trozo.
Si la superficie es cerrada, los dos colores nunca se juntan.
Si la superficie tiene límites curvos, los dos colores se encuentran solamente a lo largo de estas curvas.
Un bicho que se arrastrara sobre tal superficie y tuviera prohibido cruzar las curvas límites, si existen, siempre quedaría en la misma cara.
A. F. Möbius hizo el sorprendente descubrimiento de que existen superficies con una sola cara.
La mas simple de estas superficies es la llamada banda de Möbius, formada tomando una larga tira rectangular de papel y uniendo sus extremos después de darle media vuelta.
Un bicho que se arrastrara sobre esta superficie, andando siempre por la parte media de la tira, llegaría a su posición original en el lado inferior, como se aprecia en el dibujo del artista gráfico M. C. Escher (1898-1972)
Otra propiedad curiosa de la banda de Möbius es que su contorno está formado por una curva simple cerrada.
La superficie ordinaria de dos lados, formada uniendo los extremos de un rectángulo sin retorcerlo, tiene dos contornos curvos distintos.
Si esta última tira se corta a lo largo de la línea central, se rompe en dos tiras distintas de la misma clase. Pero si se corta la banda de Möbius a lo largo de esta línea, encontramos que queda de una sola pieza.
Resulta difícil, para cualquiera que no esté familiarizado con la banda de Möbius, predecir este comportamiento, tan contrario a la intuición de lo que "debería" suceder.
Si la superficie que resulta de cortar la banda de Möbius a lo largo de su línea media se corta otra vez a lo largo de dicha línea media, se forman dos tiras, separadas pero entrelazadas.
Es fascinante jugar con tales tiras, cortándolas de parte a parte a lo largo de líneas paralelas al contorno a distancias de 1/2, 1/3, etc.
Ciertamente, la banda de Möbius merece un lugar en la instrucción geométrica elemental.
botella de Klein es una superficie no orientable abierta cuya característica de Euler es igual a 0 ; no tiene interior ni exterior. Otros objetos no-orientables relacionados son la banda de Möbius y el plano proyectivo real. Mientras que una banda de Möbius es una superficie con borde, una botella de Klein no tiene borde. Tampoco lo tiene una esfera, aunque ésta sí es orientable.
La botella de Klein fue descrita por primera vez en 1882 por el matemático alemán Felix Klein. El nombre original del objeto no fue el de botella de Klein (en alemán Kleinsche Flasche), sino el de superficie de Klein (en alemán Kleinsche Fläche). El traductor de la primera referencia al objeto del alemán al inglés confundió las palabras. Como la apariencia de la representación tridimensional recuerda a una botella, casi nadie se dio cuenta del error.
Construcción
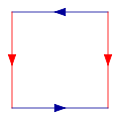
Comenzamos con un cuadrado, y pegamos los bordes coloreados en el diagrama siguiente, de modo que las flechas coincidan. Más formalmente, la botella de Klein es el cociente del cuadrado [0,1] × [0,1] con sus bordes identificados por la relación (0, y) ~ (1, y) para 0 ≤ y ≤ 1, y (x, 0) ~ (1 − x, 1) para 0 ≤ x ≤ 1:
Este cuadrado es el polígono fundamental de la botella de Klein.
Nótese que éste es un pegado "abstracto" en el sentido de que, al tratar de hacerlo en tres dimensiones, resulta una botella de Klein que se autointerseca. La botella de Klein, propiamente dicha, no tiene autointersecciones. No obstante, hay un modo de visualizar la botella de Klein como figura en cuatro dimensiones.
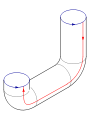
Para ello, pegamos las flechas rojas del cuadrado, (lados derecho e izquierdo) resultando un cilindro. Para pegar los extremos de manera que las flechas de los círculos coincidan, pasamos un extremo por el lado del cilindro. Nótese que esto crea una autointersección circular. Esta es una inmersión de la botella de Klein en tres dimensiones.
Añadiendo una cuarta dimensión al espacio tridimensional, conseguimos que la botella pase a través de sí misma sin necesidad de un agujero. Para ello empujamos suavemente un trozo de tubo que contenga la intersección fuera del espacio tridimensional original. Una analogía útil es considerar una curva que se autointerseca en el plano; las intersecciones se pueden eliminar levantando una línea fuera del mismo.
Esta inmersión es útil para visualizar muchas propiedades de la botella de Klein. Por ejemplo, no tiene borde (donde la superficie se detenga abruptamente), y no es orientable, al tener su inmersión una sola cara.
Cono fibrado
Esta superficie (simbolizada por  ) puede considerarse como el espacio total de un fibrado (no trivial) sobre el círculo donde la fibra es también un círculo, i.e.
) puede considerarse como el espacio total de un fibrado (no trivial) sobre el círculo donde la fibra es también un círculo, i.e.  . En contraste el toro también es un fibrado, pero es trivial, esto es
. En contraste el toro también es un fibrado, pero es trivial, esto es  .
.
 ) puede considerarse como el espacio total de un fibrado (no trivial) sobre el círculo donde la fibra es también un círculo, i.e.
) puede considerarse como el espacio total de un fibrado (no trivial) sobre el círculo donde la fibra es también un círculo, i.e.  . En contraste el toro también es un fibrado, pero es trivial, esto es
. En contraste el toro también es un fibrado, pero es trivial, esto es  .
.Sección
Seccionando una botella de Klein en dos mitades a lo largo de su plano de simetría resultan dos bandas de Möbius, cada una imagen especular de la otra. Una de ellas es la imagen de la derecha. Recuerde que la intersección de la imagen no está realmente allí. De hecho, también es posible cortar la botella de Klein en una única banda de Möbius.
Otro concepto con el mismo nombre
En la geometría algebraica, una superficie de Klein, que se diferencia de la botella de Klein, es el similar de una superficie de Riemann en el sentido de que una superficie de Klein admite una estructura di-analítica, es decir una estructura analítica que adiciona una posible función de transición a una estructura analítica -consistente en la conjugación compleja- determina una que es anti-analítica.
Una representación bidimensional de la Botella de Klein inmersa en el espacio tridimensional.
La botella de Klein: geometría ‘palindrómica’
La botella de Klein es un ejemplo de superficie (variedad topológica de dimensión 2) compacta (cerrada y acotada), conexa (de una pieza) y no orientable (contienebandas de Möbius).
Un precioso resultado sobre superficies compactas y conexas afirma que cualquiera de ellas puede obtenerse como el cociente de una región poligonal en el plano con un número par de aristas identificadas dos a dos (ver [2] páginas 8 a 16). En particular, la botella de Klein es el cociente de un cuadrado cuyos lados están identificados como muestra la figura:

Vamos a ver unas cuantas propiedades de la botella de Klein ayudándonos del cuentoBotella de Klein deJuan José Arreola (1918-2001); se reproduce el texto íntegramente y añadimos después algunas notas explicativas.
–oOo–
BOTELLA DE KLEIN
“El cilindro es al toro lo que la Banda de Moebius a la Botella de Klein”(1). Y Francisco Medina Nicolau sacó de una gaveta la célebre cinta de papel, ahora con las puntas pegadas de un modo particular, como en un cuello de camisa. Sus manos de prestidigitador la hicieron girar y en el aire quedó la forma pura:– Cuando la Banda de Moebius se esconde en ella misma, surge la Botella de Klein… ¿La ves?Quedé perplejo y salí por tangente literaria:– Es el procedimiento de Kafka, según la ley de Roberto Wilcock: sacarse de la cabeza un objeto, escamotearlo y seguir hablando sobre él…El doctor Garfias estaba presente.– A propósito de cabeza, no se la quiebre usted, que al fin y al cabo la botella es de vidrio. La inventaron los alquimistas. Creo que fue Jehan Brodel, denunciado a la Inquisición por sus vecinos de la calle del Pot de Fer ¿se acuerda usted? El cuerpo infame sin principio ni fin era la imagen blasfematoria de Dios. Fue destruido el original y los dibujos previos también. Pero la cosa llegó si no a los ojos, a los oídos del Bosco(2), que pintaba de memoria: allí está el ámpula, la burbuja de jabón que encierra a los amantes en el Jardín de las Delicias…Ludlow llegó en ese momento con envoltorio sospechoso y sonrisa feliz. Había alcanzado a oír las palabras de Garfias y enlazó los puntos suspensivos:–… la botella figura también dentro de la tradición castellana. Es el fracaso del Marqués de Villena citado por Quevedo y por Vélez de Guevara. Es la redoma que encerraba al Homúnculo, el feto infernal, el niño que no necesita madre para nacer…Mis tres doctores en física, topología y lógica(3) me acorralaron en una superficie collado sin pies ni cabeza. Hicieron y deshicieron nudos imaginarios y reales con cuerdas y palabras. Yo dije, recordando a Rafael, que el collado se parece al fuste de una silla de montar y que los artesanos de Colima trazan la superficie sobre pergaminos como Dios les da a entender sirviéndose de patrones heredados. Se rieron. Jorge Ludlow desenvolvió su paquete.– ¿Quería una Botella de Klein?No paso a creerlo. Siguiendo indicaciones precisas, los diseñadores y obreros de la casa Pyrex(4), especializada en materiales refractarios, me hicieron el capricho. No paso a creerlo. Después de muchas tentativas, aquí está el milagro físico sin interior ni exterior, perfectamente soplado y sin defecto.Ahora estoy sólo frente al objeto irracional, llenándolo con mis ojos antes de ponerle tinto de Borgoña. Aquí está sobre mi mesa de ¿trabajo? la Botella de Klein que busqué por más de veinte años de ¿trabajo?Mi mente trabajada no puede más, siguiendo las curvas del palindroma de cristal. ¿Eres un cisne que se hunde el cuello en el pecho y se atraviesa para abrir el pico por la cola? Me emborracho mentalmente gota a gota con la clepsidra que llueve lentamente sus monosílabos de espacio y tiempo. Mojo la pluma en ese falso tintero y escribo sin mano una por una las definiciones inútiles: signos de interrogación estatuaria. Trompa gigante de Falopio. Corno de caza que me da el toque de atención al silencio, cuerno de la abundancia vacía, cornucopia rebosante de nada… Víscera dura que desdice la vida diciendo soy útero y falo, la boca que dice estas cosas: soy tu yo de narciso inclinado a su lirio, tu dentro y tu fuera, abierto y cerrado, tu liberación y tu cárcel, no bajes los ojos ¡mírame!Pero ya no puedo mirar porque la cabeza se me fue a las entrañas, ¿porque los topólogos no trabajan con vísceras y desarrollan hígados, riñones y asas intestinales en vez de nudos y toros? Se lo voy a proponer si despierto mañana.Por ahora empuño la Botella de Klein. La empuñas, pero no la empinas. ¿Cómo puedo beber al revés? Tienes miedo en pie como falso suicida, jugando metafísico el peligroso juguete en tus manos, revólver de vidrio y vaso de veneno… Porque tienes miedo de beberte hasta el fondo, miedo de saber a qué sabe tu muerte, mientras te crece en la boca el sabor, la sal del dormido que reside en la tierra…
–oOo–
NOTAS
(1) El toro (la superficie) se obtiene a partir de un cuadrado haciendo las identificaciones que se indican en la figura 2:

Es decir, el toro se obtiene identificando las dos circunferencias que forman el borde del cilindro de la figura 2. Para construir la botella de Klein, podrían haberse identificado en primer lugar los dos lados marcados en azul (figura 1): se habría obtenido así una banda de Möbius, cuyo borde debería identificarse siguiendo las indicaciones de las flechas rojas. En el video de debajo se explica con gran claridad cómo se obtiene la botella de Klein con el proceso indicado en la figura 1; después se corta por la línea roja (también en topología cortar es el proceso inverso a pegar: se estaría deshaciendo el cilindro obtenido en primer lugar) y se obtiene una banda de Möbius.
(2) Observad el panel central de El Jardín de las Delicias: en el relato se refiere a la zona marcada en el cuadro, el ámpula en la que se sitúan los amantes, ¿una botella de Klein?


(3) Se refiere a Francisco Medina Nicolau (1929-2001) físico mexicano, el Doctor Garfias y Jorge Ludlow, con los que comparte esta ‘reunión científica’.
(4) La botella de Klein no vive en dimensión 3. En la figura 1, y en todas las representaciones de esta superficie, se autointerseca al realizar la identificación. Esta es la prueba de que no puede embeberse (incluirse de manera ‘fiel’) en el espacio en el que vivimos. La botella de Klein vive de manera natural en dimensión 4. Los obreros de la casa Pyrex –aunque no dudo de su profesionalidad– no pueden hacer milagros: el mejor fabricante de botellas de Klein en vidrio que conozco es el físico Cliff Stoll (figura 5) que mantiene la página ACME Klein Bottles; sus magníficas botellas, aunque preciosas, son en realidad una proyección en 3D de esta superficie no orientable.
Botella de Klein encierra numerosas metáforas (ver [3]): el narrador acaba entrando dentro de la botella de Klein, o transformándose en ese objeto, que califica deirracional.


![\begin{cases}
x(u,v)=\left[1+\cfrac{v}{2}\cos\cfrac{u}{2}\right]\cos(u)\\
y(u,v)=\left[1+\cfrac{v}{2}\cos\cfrac{u}{2}\right]\sin(u)\\
z(u,v)=\cfrac{v}{2}\sin\cfrac{u}{2} \end{cases}](https://upload.wikimedia.org/math/9/3/d/93d42cdd12703fe0bcd90dcaabf3278b.png)

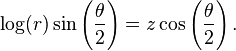



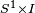 y
y 




No hay comentarios:
Publicar un comentario