El conjunto de Mandelbrot es el más conocido de los conjuntos fractales y el más estudiado. Se conoce así en honor al matemático Benoît Mandelbrot (1924-2010), que investigó sobre él en los años setenta.
Este conjunto se define así, en el plano complejo:
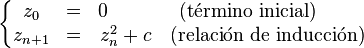
Si esta sucesión queda acotada, entonces se dice que c pertenece al conjunto de Mandelbrot, y sino, queda excluido del mismo.
Por ejemplo, si c = 1 obtenemos la sucesión 0, 1, 2, 5, 26… que diverge. Como no está acotada, 1 no es un elemento del conjunto de Mandelbrot.
En cambio, si c = –1 obtenemos la sucesión 0, –1, 0, –1,… que sí es acotada, y por tanto, –1 sí pertenece al conjunto de Mandelbrot.
A menudo se representa el conjunto mediante el algoritmo de tiempo de escape. En ese caso, los colores de los puntos que no pertenecen al conjunto indican la velocidad con la que diverge (tiende al infinito, en módulo) la sucesión correspondiente a dicho punto. En la imagen de ejemplo, observamos que el rojo oscuro indica que al cabo de pocos cálculos se sabe que el punto no está en el conjunto mientras que el blanco informa de que se ha tardado mucho más en comprobarlo. Como no se puede calcular un sinfín de valores, es preciso poner un límite y decidir que si los p primeros términos de la sucesión están acotados entonces se considera que el punto pertenece al conjunto. Al aumentar el valor de p se mejora la precisión de la imagen.
Por otra parte, se sabe que los puntos cuya distancia al origen es superior a 2, es decir,  no pertenecen al conjunto. Por lo tanto basta encontrar un solo término de la sucesión que verifique |zn| > 2 para estar seguro de que c no está en el conjuto.
no pertenecen al conjunto. Por lo tanto basta encontrar un solo término de la sucesión que verifique |zn| > 2 para estar seguro de que c no está en el conjuto.
 no pertenecen al conjunto. Por lo tanto basta encontrar un solo término de la sucesión que verifique |zn| > 2 para estar seguro de que c no está en el conjuto.
no pertenecen al conjunto. Por lo tanto basta encontrar un solo término de la sucesión que verifique |zn| > 2 para estar seguro de que c no está en el conjuto.Introducción: explorando la autosimilitud
Una propiedad fundamental de los fractales es la autosimilitud o autosemejanza, que se refiere a una cierta invariabilidad con relación a la escala, o dicho de otro modo, al acercarse a ciertas partes de la imagen reaparece en miniatura la imagen total. Un mismo motivo aparece a distintas escalas, a un número infinito de escalas.
Veámoslo más en detalle, a partir del plano siguiente (derecha):
Veámoslo más en detalle, a partir del plano siguiente (derecha):
Al agrandar el cuadro verde, se obtiene la imagen de la izquierda, donde:
- Salta a la vista que la bola negra a es una reducción exacta de la bola A. La protuberancia a la izquierda de a también es una reducción exacta de a, y el proceso sigue indefinidamente.
- También se puede observar que la bola b es una reducción de A (una reducción combinada con una rotación, es decir que b se obtiene de A mediante una semejanza). Mirando mejor, se nota un sinfín de protuberencias semejantes a A.
Volviendo al plano, escojamos esta vez el cuadro azul oscuro situado en el extremo izquierdo del plano. Al agrandarlo, obtenemos la imagen de la derecha:
Su parecido a la imagen inicial es obvio. El proceso se puede repetir un sinfín de veces, empezando por agrandar la pequeña mancha negra a la izquierda del cuadro.
Ahora, ampliemos el cuadrito violeta del plano, y obtendremos la imagen de la izquierda:
En esta imagen aparece una mancha arriba a la izquierda que tiene la misma forma que la imagen inicial. Al mirar más de cerca, se obtiene la imagen de abajo a la derecha. Y una vez más, el parecido salta a la vista.
Ahora, agrandemos el cuadro azul claro de la derecha del plano (imagen de la derecha):
Acerquémonos al cuadro blanco de la última imagen (a la izquierda):
Aquí se nota una ligera deformación de la figura inicial. Sin embargo, esta imagen sigue siendoisomorfa a la inicial. Y claro, alrededor de cada clon de la forma inicial existen otros clones minúsculos, en las mismas posiciones relativas que en la figura global. El proceso no tiene fin.
- Otra representación
En esta imagen, el conjunto es, naturalmente, el mismo, pero las líneas de nivel (que separan los colores, fuera del conjunto) no son idénticas. Esto se debe a que no se ha empleado el mismo criterio de divergencia: en esta imagen es realmente |zn| > 2, mientras que en las anteriores era |zn| > 10, por razones estéticas, ya que así se obtiene una imagen inicial menos oscura.
Historia
La teoría básica sobre la iteración de funciones complejas fue desarrollada por Gaston Julia y Pierre Fatou en losaños 1910. La forma extraordinariamente intrincada de conjuntos relacionados con estas iteraciones se reveló en el momento en que los gráficos por ordenador fueron lo suficientemente avanzados. Las primeras imágenes del conjunto, algo burdas, de Robert Brooks y Peter Matelski, datan de 1978.1
Benoit Mandelbrot estudió el espacio de parámetros de polinomios cuadráticos en un artículo aparecido en 1980 y despertó el interés global por el mismo.2
El estudio matemático riguroso de este conjunto realmente comenzó con el trabajo de los matemáticos Adrien Douady y John H. Hubbard,3 4 quienes demostraron muchas de sus propiedades fundamentales y nombraron el conjunto en honor de Mandelbrot. Entre otras propiedades, probaron que es un conjunto conexo y formularon la conjetura MLC, que formula la creencia de que el conjunto de Mandelbrot es localmente conexo.
Relación con los conjuntos de Gaston Julia
Existe otra manera de definir este conjunto: es el conjunto de los complejos c para los que el conjunto de Julia asociado a fc(z) = z² + c es conexo.
Imágenes calculadas con ordenador digital
Hasta que no aparecieron los primeros ordenadores digitales no se pudo visualizar este fractal Z = Z2 + C con toda su complejidad.
En la serie que se detalla debajo podemos ver cómo va mejorando la definición del fractal, a medida que incrementamos el número de iteraciones. Los puntos que convergen a un valor determinado aparecen de color amarillo pálido, y pertenecen propiamente al conjunto de Mandelbrot. Los puntos que presentan divergencia al infinito se han coloreado con una gama cromática que va desde el gris al negro, en función del número de iteraciones necesarias (algoritmo de la velocidad de escape). Cuantas menos iteraciones son necesarias para divergir al infinito, se aplica un color más oscuro.
Propiedades
Propiedades topológicas
El conjunto de Mandelbrot es compacto, conexo y su complemento también es conexo. Su interior, al igual que cualquier interior de un subconjunto de  no vacío, resulta ser de la cardinalidad de
no vacío, resulta ser de la cardinalidad de  , esto es una consecuencia directa de que la topología usual en
, esto es una consecuencia directa de que la topología usual en  tiene una base de abiertos de cardinalidad no numerable =
tiene una base de abiertos de cardinalidad no numerable = 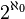 .
.
 no vacío, resulta ser de la cardinalidad de
no vacío, resulta ser de la cardinalidad de  , esto es una consecuencia directa de que la topología usual en
, esto es una consecuencia directa de que la topología usual en  tiene una base de abiertos de cardinalidad no numerable =
tiene una base de abiertos de cardinalidad no numerable = 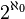 .
.
Su frontera tiene dimensión topológica 1 pero dimensión de Hausdorff 2, la máxima posible al ser subconjunto del plano.
Este es el dibujo original que Mandelbrot descubrió a la comunidad científica a finales de los 70 cuando trabajaba en el centro de investigación Thomas J. Watson. Ahora disponemos de imágenes más detalladas como las representadas en la  tabla de abajo. Si ampliamos las verrugas, nos toparemos con la primera sorpresa: son diminutas copias del conjunto original, mini-mandelbrots. No exactamente idénticas, pero sí semejantes. Y como no, a su vez, estas copias están llenas de verrugas cada una de las cuales vuelve a ser un conjunto de Mandelbrot al ser ampliadas, y así ad nausean...
tabla de abajo. Si ampliamos las verrugas, nos toparemos con la primera sorpresa: son diminutas copias del conjunto original, mini-mandelbrots. No exactamente idénticas, pero sí semejantes. Y como no, a su vez, estas copias están llenas de verrugas cada una de las cuales vuelve a ser un conjunto de Mandelbrot al ser ampliadas, y así ad nausean...
En la tabla inferior puedes ver un ejemplo de la existencia de pequeñas réplicas similares al propio conjunto inicial en su interior. Hemos utilizado Fractint con mapa de color blues.map para generar las imágenes. Partiendo del conjunto inicial hemos ido haciendo sucesivas ampliaciones de izquierda a derecha en las tres primeras imágenes y de derecha a izquierda en las siguientes.
Y aquí puedes observar el efecto zoom en forma de película.
Mientras que los conjuntos de Julia son estrictamente autosimilares, los pequeños conjuntos de Mandelbrot sembrados en sus profundidades son solo cuasi-autosimilares. El grado de similaridad depende de la zona y el grado de magnificación al que nos encontremos de forma no trivial.
Vamos a describir el protocolo para la creación del conjunto. El proceso iterativo queda descrito por el mapa:
donde tanto z como c son complejos. Al contrario de las actuaciones previas con los biomorfos o los conjuntos de Julia, el conjunto de Mandelbrot en realidad no es la iteración de una sola función, sino de infinitas funciones. Como hemos visto el factor que determina si un conjunto de Julia es conexo o disconexo es el valor de c.
Para determinar que valores de c producen conjuntos conexos y cuales disconexos parece que no nos quede más remedio que determinar cada conjunto iterando todos los puntos del plano complejo para cada función f_c=z2 +c. Afortunadamente se puede demostrar que basta con iterar el (0,0) para cada función f_c y la órbita nos determina la conectividad del conjunto.
Si la órbita del origen (condición inicial z_0=(0,0)) para la iteración de f_c no escapa al infinito, entonces:
- (1) o bien pertenece al conjunto de Julia de f_c,
(2) o bien está atrapado.
En el primer caso el conjunto de Julia correspondiente será dendrítico. En el segundo caso el conjunto será equivalente, topológicamente a un círculo y por tanto el conjunto será conexo. El conjunto de todos los valores c tales que sus correspondientes conjuntos de Julia son conexos forman en el plano complejo el famoso conjunto de Mandelbrot. @@
En la figura superior están representados algunos conjuntos de Julia con valores de c indicados en el plano complejo por las líneas de color azul. Para valores de c dentro del conjunto de Mandelbrot la forma de los conjuntos de Julia es semejante a círculos. Fuera del conjunto tenemos nubes de puntos disconexos. Los conjuntos de Julia más interesantes estéticamente se observan en la frontera. Las formas dendríticas de los conjuntos de Julia corresponden a las fronteras filamentosas del conjunto de Mandelbrot. En la imagen inferior puedes observar un gif animado del efecto de la variación continua del parámetro c en las formas de los conjuntos J a lo largo de una línea que va desde la frontera de M (forma dendrítica) hasta su interior (forma circular).














No hay comentarios:
Publicar un comentario