En geometría las medianas (en algunos países también llamadas transversales de gravedad[cita requerida]) de un triángulo son, cada uno de los tres segmentos que unen cada vértice con el punto medio de su lado opuesto.

Las medianas de un triángulo (líneas rojas) se cortan en el baricentro del mismo.
Propiedades
Las medianas tienen las siguientes propiedades:
- Cada mediana divide al triángulo en dos triángulos, de los cuales es un lado común; dichos triángulos, en general, no son congruentes, pero sí de igual área, por ejemplo para el caso de la mediana AI (véase la figura) dichas regiones son los dos triángulos ΔABI y ΔACI de igual área.
- Una línea isogonal a la mediana respecto a los lados que parten del vértice respectivo se llama simediana y la intersección de las tres simedianas se llama punto simediano, que es punto isogonal del punto mediano o centroide.1
- Las tres medianas se intersecan en un único punto, llamado el baricentro, gravicentro [cita requerida], o centroide, punto mediano2 marcado con G en la figura.
- Dos tercios de la longitud de cada mediana están entre el vértice y el baricentro, mientras que el tercio restante está entre el baricentro y el punto medio del lado opuesto.
- Para cualquier triángulo (euclidiano) con lados
 , medianas
, medianas  y perímetro
y perímetro  , se cumple la siguiente desigualdad:3
, se cumple la siguiente desigualdad:3
- Para cualquier triángulo (euclidiano) con lados
 y medianas
y medianas  ,
,  la proyección de
la proyección de 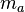 sobre a, los elementos indicados verifican las siguientes ecuaciones:3
sobre a, los elementos indicados verifican las siguientes ecuaciones:3




Relación con el centro de gravedad
Cada una de las tres medianas de un triángulo pasa por el centroide del mismo, el cual es coincidente con el centro de gravedad de un objeto con forma de triángulo (si éste es de densidad uniforme). Así, dicho objeto estaría en equilibrio en cualquier transversal de gravedad (línea que pase a través del centro de gravedad ), Las medianas son solo tres transversales de gravedad, del grupo infinito de transversales de gravedad del triángulo.
Experimental
- Si recortamos una región triangular de cartón homogéneo ( en especial de espesor uniforme), y la apoyamos sobre la punta del dedo índice, comúnmente, el cartón caerá, aunque se mantendrá estable si y solo si el punto de apoyo coincide con el baricentro.5
- Además, si se suspenden tres tubos fluorescentes en triángulo, con cables de peso despreciable, de un punto S, la vertical del punto S cortará el plano del triángulo de los tubos, por el baricentro de dicho triángulo.6
Teorema de la mediana
En geometría, el teorema de Apolonio, también llamado teorema de la mediana, es un teorema que relaciona la longitud de la mediana de un triángulo con las longitudes de sus lados.
|
Para cualquier triángulo ΔABC (véase fig. m1), si M es la mediana correspondiente al lado c, donde AP =PB = ½ c, entonces :
Medianas (fórmulas de aplicación práctica)
Del teorema de Apolonio, también llamado "teorema de la mediana", pueden deducirse varias fórmulas prácticas (válidas para cualquier triángulo). Éstas permiten calcular a partir del conocimiento de tres elementos, a un cuarto elemento desconocido, (los elementos en cuestión son lados y medianas). La siguiente tabla muestra un resumen de las mismas (con notación acorde a la figura de la propia tabla) :
 | 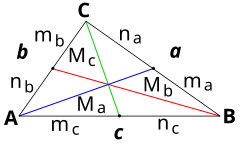 | ||
 | |||
 | |||
 |  |  | |
 |  |  | |
 |  |  | |
| |||
En el triángulo isósceles
-
 ;
;  8
8
En el triángulo rectángulo
Triángulo mediano
Se conoce con el nombre de triángulo mediano respecto a otro triángulo al que tiene como vértices los puntos medios de un triángulo cualquiera dado.
Proposiciones
- Los lados de un triángulo mediano son las bases medias de un triángulo dado.
- El baricentro de un triángulo coincide con el baricentro del triángulo mediano.
- El área de un triángulo mediano es 1/4 del área del triángulo original.
- Un triángulo mediano es semejante al triángulo inicial11
- En cualquier triángulo isósceles la mediana correspondiente a la base es a la vez altura y bisectriz y es parte de la línea mediatriz de tal base.12
Mediana de un trapecio
En cualquier trapecio, se llama mediana al segmento que une los puntos medios de los lados no paralelos. Recibe también el nombre de paralela media.13
- La mediana del trapecio es paralela a las bases e igual a la semisuma de las mismas.
La Mediana es cada una de las rectas que une el punto medio de un lado con el vértice opuesto.
El punto de corte de las tres medianas se llama baricentro.
Ejercicio
Hallar las ecuaciones de las medianas y el baricentro del triángulo de vértices: A(2, 0), B(0, 1) y C(-3, -2).
Ecuación de la mediana que pasa por A y el punto medio de BC
En primer lugar hallamos el punto medio de Bc
Calculamos la ecuación de la recta que pasa por dos puntos.
Ecuación de la mediana que pasa por B y el punto medio de AC
Ecuación de la mediana que pasa por C y el punto medio de AB
Baricentro
El nombre deriva del término griego orto, que quiere decir recto, en referencia al ángulo formado entre las bases y las alturas.1
El ortocentro se encuentra en el interior del triángulo si éste es acutángulo; coincide con el vértice del ángulo recto si es rectángulo, y se halla en el exterior del triángulo si es obtusángulo.
Dado un triángulo cualquiera (excluyendo un triángulo rectángulo), el 'triángulo órtico o triángulo pedal respecto del dado, es el que tiene por vértices los pies de las tres alturas de éste, es decir, las proyecciones de los vértices sobre los lados.*El ortocentro de un triángulo es el incentro de su triángulo órtico (como se observa en la figura).
- El ortocentro es el incentro del triángulo órtico (como se observa en la figura).
- Las alturas de un triángulo son las bisectrices de los ángulos del triángulo pedal.2
- En el caso de un triángulo rectángulo, las alturas de los ángulos agudos tienen como un pie común: el vértice del ángulo recto, que con el pie sobre la hipotenusa, a lo más, forman un segmento, en este caso no hay triángulo pedal.
Construir el ortocentro de un triángulo
|



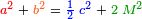 ).
).




No hay comentarios:
Publicar un comentario