En matemáticas, dos figuras de puntos son congruentes si tienen los lados iguales y el mismo tamaño (o también, están relacionados por un movimiento) si existe una isometría que los relaciona: una transformación que es de translaciones, rotaciones y reflexiones. Por así decirlo, dos figuras son congruentes si tienen la misma forma y tamaño, aunque su posición u orientación sean distintas. Las partes coincidentes de las figuras congruentes se llaman homólogas o correspondientes.

Un ejemplo de movimiento o congruencia semejante a ellas. La última no es ninguna de las dos cosas. Nótese que los movimientos cambian propiedades de las figuras homogéneas y confluentes como la posición de estas, pero dejan inalteradas otras como las distancias y los ángulos.
Definición de congruencia en geometría analítica
En la geometría euclidiana, la congruencia es fundamental; es lo equivalente a igualdad matemática en aritmética y álgebra. En geometría analítica, la congruencia puede ser definida así: dos figuras determinadas por puntos sobre un sistema de coordenadas cartesianas son congruentes si y solo si, para cualquier par de puntos en la primera figura, la distancia euclidiana entre ellos es igual a la distancia euclidiana entre los puntos correspondientes en la segunda figura.
Definición formal: Dos subconjuntos A y B de un espacio euclídeo  son llamados congruentes si existe una isometría
son llamados congruentes si existe una isometría  con
con  .
.
 son llamados congruentes si existe una isometría
son llamados congruentes si existe una isometría  con
con  .
.Ángulos congruentes
Los ángulos opuestos son congruentes debido a que una rotación de 180° sobre su vértice hace coincidir uno y el otro.
Congruencia de triángulos
Dos triángulos son congruentes si sus lados correspondientes tienen la misma longitud y sus ángulos correspondientes tienen la misma medida.
Notación: Si dos triángulos  y
y  son congruentes, entonces la relación se notará como:
son congruentes, entonces la relación se notará como:
 y
y  son congruentes, entonces la relación se notará como:
son congruentes, entonces la relación se notará como:
Criterios para deducir o establecer la congruencia de dos triángulos.
Congruencia de triángulos
Las condiciones mínimas que deben cumplir dos triángulos para que sean congruentes se establecen a través de los llamados teoremas de congruencia1 2 los cuales son:
- Caso LAL: Dos triángulos son congruentes si tienen iguales dos de sus lados respectivos y el ángulo comprendido entre ellos.
- Caso ALA: Dos triángulos son congruentes si tienen iguales dos de sus ángulos respectivos y el lado entre ellos.
- Caso LLL: Dos triángulos son congruentes si tienen iguales los tres lados.
- Caso LLA: Dos triángulos son congruentes si tienen iguales dos de sus lados respectivos y el ángulo opuesto mayor medida que ellos.
- Caso LAA: Dos triángulos son congruentes si tienen iguales uno de los lados, el ángulo opuesto a dicho lado y otro de los ángulos.
- Caso AAL: Dos triángulos son congruentes si tienen iguales dos de sus ángulos respectivos y el lado opuesto a cualquiera de los ángulos.
Congruencia de triángulos |
Observa los siguientes triángulos:
Al mirar los dos pares de triángulos se puede apreciar que en ambos los triágulos tienen entre si la misma forma y tamaño.
Cuando se cumplen estas dos condiciones se dice que los triángulos son congruentes; esta palabra (congruente) se simboliza o representa con el símbolo  .
.
Definición:
Se dice que un Δ ABC es congruente con otro Δ DEF si sus lados respectivos son iguales y sus ángulos respectivos también lo son.
Para expresar en lenguaje matemático que los dos triángulos de la izquierda son congruentes, se usa la siguiente simbología:
Al observar los triángulos de la figura puede apreciarse que tienen lados respectivamente congruentes, que son:
También tienen ángulos respectivamente congruentes:
Entonces es posible afirmar que  .
.
Al revés: si dos o más triángulos son congruentes, sus lados y ángulos lo serán respectivamente, en el orden de las letras asignadas a sus vértices para nombrarlos, salvo que gráficamente se indique otra correspondencia.
Si, por ejemplo, tenemos Δ ABR  Δ CDS, sus lados respectivamente congruentes serán:
Δ CDS, sus lados respectivamente congruentes serán:
Y los ángulos respectivamente congruentes serán:
Criterios de congruencia
Los criterios de congruencia corresponden a los postulados y teoremas que enuncian cuáles son las condiciones mínimas que deben reunir dos o más triángulos para que sean congruentes.
Estas son:
1.- Congruencia de sus lados
2.- Congruencia de sus ángulos
Para que dos triángulos sean congruentes, es suficiente que sólo algunos lados y/o ángulos sean iguales.
Los postulados o criterios básicos de congruencia de triángulos son:
Postulado LAL
LAL significa lado-ángulo-lado.
Dos triángulos son congruentes si tienen dos lados y el ángulo determinado por ellos respectivamente iguales.
Postulado ALA
ALA significa ángulo-lado-ángulo.
Dos triángulos son congruentes si tienen dos ángulos y el lado común a ellos, respectivamente, iguales.
Postulado LLA
LLA significa lado-lado-ángulo
Dos triángulos son congruentes si tienen respectivamente iguales dos lados y el ángulo opuesto al mayor de ellos.
Postulado LLL
LLL significa lado-lado-lado.
Dos triángulos son congruentes si tienen sus tres lados respectivamente iguales.
En geometría proyectiva, el teorema de Desargues, llamado así en honor a Gérard Desargues, expone:
|
Considere los triángulos ABC y DEF. El que los triángulos sean proyectivos desde un punto significa que las rectas AD, BE y CF concurren en un mismo punto O. De modo parecido, el que los triángulos sean proyectivos desde una recta significa que los pares de lados (AB, DE), (BC, EF) y (AC, DF) se cortan respectivamente sobre una misma recta r.
Al punto O se le llama centro de perspectiva y a la recta r, eje de perspectiva.

| Teorema de Desargues: Sean ABC y A’B’C’ dos triángulos con vértices y aristas diferentes. Los puntos de intersección de las rectas que forman las aristas tomadas dos a dos, es decir los puntos P = AB ÇA’B’, Q = BC ÇB’C’ y R = ACÇA’C’, están alineados si y sólo si las rectas AA’, BB’ y CC’son concurrentes. |
La razón doble de cuatro puntos alineados A, B, C, D se define como (A,B,C,D) =  siendo
siendo  la distancia orientada (es decir, con signo) entre A y C, etc. Cuatro puntos A, A’, B y B’ decimos que forman una cuaterna armónica (o equivalentemente que B’ es el conjugado armónico de B con respecto a A y A’) si y sólo si (A,A’,B,B’) = - 1.
la distancia orientada (es decir, con signo) entre A y C, etc. Cuatro puntos A, A’, B y B’ decimos que forman una cuaterna armónica (o equivalentemente que B’ es el conjugado armónico de B con respecto a A y A’) si y sólo si (A,A’,B,B’) = - 1.
Comprobemos con Cabri que la razón doble permanece invariante por proyecciones, y que es, por tanto, un invariante proyectivo. De hecho, en dimensión uno es equivalente dar una estructura proyectiva a asignar razón doble de cada elemento respecto de tres elementos fijados, y una aplicación es una trasformación proyectiva si y sólo si conserva la razón doble.
| Consideramos un punto P y una recta r. Tomamos cuatro puntos de r que denotamos por 1, 2, 3, 4 y calculamos (usando el macro "razon doble") su razón doble. Proyectamos los cuatro puntos desde P y obtenemos cuatro rectas a1, a2, a3, a4. Cortamos estas rectas con otra recta cualquiera r’ y calculamos la razón doble de los puntos de intersección 1’, 2’, 3’, 4’. Observamos que ambas razones dobles son iguales. |
Esto nos permite asignar razón doble a cuatro rectas a1, a2, a3, a4 de un haz, cortando con una recta cualquiera r y calculando la razón doble de los puntos de intersección. Por lo que acabamos de ver, esta razón doble sólo depende de las rectas a1, a2, a3, a4 y no de la recta r elegida.
De esta forma vemos que un haz de rectas tiene una estructura proyectiva, y dada una recta que no esté en el haz, la aplicación que a cada recta del haz le hace corresponder el punto de intersección con esta recta es una transformación proyectiva (porque conserva la razón doble).

 y
y  son congruentes y opuestos por el vértice.
son congruentes y opuestos por el vértice.

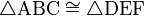
No hay comentarios:
Publicar un comentario