coeficiente es un factor vinculado a un monomio. Dado un divisor del monomio, el coeficiente es el cociente del monomio por el divisor. Así el monomio es el producto del coeficiente y el divisor. Los diferentes coeficientes dependerán de la factorización del monomio.
Un coeficiente numérico es un factor constante de un objeto específico. Por ejemplo, en la expresión 9x2, el coeficiente de x2 es 9. En álgebra elemental, coeficientes numéricos de términos semejantes se agrupan para simplificar las expresiones algebraicas..
El objeto puede ser cosas tales como una variable, un vector, una función, etc. En algunos casos, los objetos y los coeficientes están ordenados de la misma manera, dando lugar a expresiones tales como:
donde an es el coeficiente de la variable xn para cada n = 1, 2, 3, …
En un polinomio P(x) de una variable x, el coeficiente de xk puede ordenar por k, dando por ejemplo:
Para el mayor valor de k, donde ak ≠ 0, ak se denomina primer coeficiente de P, ya que la mayor parte de las veces, los polinomios se escriben a partir de la izquierda, con la mayor potencia de x. Así, por ejemplo, el primer coeficiente del polinomio:
es 4.
Los coeficientes de los polinonios también pueden estar en otro orden:
- 9x2+9+6
y debe ser a0 ≠ 0 y a0 es el primer coeficiente de Q.
Coeficiente binomial
Importantes coeficientes en matemáticas incluyen los coeficientes binomiales que son los coeficientes en la declaración del teorema del binomio. Estos se pueden encontrar parcialmente con el triángulo de Pascal. Por ejemplo,
El coeficiente 4 en los términos de xbyc - xcybes conocido como el coeficiente binomial 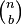 o
o  (los dos tienen el mismo valor).
(los dos tienen el mismo valor).
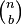 o
o  (los dos tienen el mismo valor).
(los dos tienen el mismo valor).Álgebra lineal
En álgebra lineal, el primer coeficiente de una fila en una matriz es la primera entrada no nula en aquella fila. Así, por ejemplo, dado:
El primer coeficiente de la primera fila es 1; 2 es el primer coeficiente de la segunda fila; 4 es el primer coeficiente de la tercera fila, y la última fila no tiene ningún coeficiente.
Aunque los coeficientes con frecuencia sean vistos como constantes en el álgebra elemental, con mayor frecuencia suelen ser variables. Por ejemplo, las coordenadas  de un vector (física) v en un espacio vectorial con base
de un vector (física) v en un espacio vectorial con base  , son los coeficientes de los vectores de la base en la expresión
, son los coeficientes de los vectores de la base en la expresión
 de un vector (física) v en un espacio vectorial con base
de un vector (física) v en un espacio vectorial con base  , son los coeficientes de los vectores de la base en la expresión
, son los coeficientes de los vectores de la base en la expresiónAplicación en el cálculo diferencial
Si se quiere hallar la derivada de la función cuadrática  , se desarrolla el binomio
, se desarrolla el binomio  . El coeficiente del término en
. El coeficiente del término en  que es
que es  es la derivada de
es la derivada de  . Obsérvese que si consideramos el trinomio del desarrollo como dependiente de
. Obsérvese que si consideramos el trinomio del desarrollo como dependiente de  , el término lineal es
, el término lineal es  .
.
 , se desarrolla el binomio
, se desarrolla el binomio  . El coeficiente del término en
. El coeficiente del término en  que es
que es  es la derivada de
es la derivada de  . Obsérvese que si consideramos el trinomio del desarrollo como dependiente de
. Obsérvese que si consideramos el trinomio del desarrollo como dependiente de  , el término lineal es
, el término lineal es  .
.Notación científica
La notación científica se usa para representar números reales. Siendo r el número real a representar, la representación en notación científica está compuesta de tres partes:

- c. El coeficiente, conformado por un número real con un solo dígito entero seguido de una coma (o punto) y de varios dígitos fraccionarios.
- b. La base, que en nuestro sistema decimal es 10, y en el sistema binario de los computadores es 2.
- e. El exponente entero, el cual eleva la base a una potencia.
Coeficiente | |
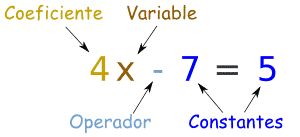 | Un número usado para multiplicar una variable Ejemplo: 4y significa 4 veces y, donde y es una variable, por lo tanto 4 es un coeficiente. |
El coeficiente es cualquier factor que se encuentre antes del número o signo en cuestión. El coeficiente puede ser numérico o literal.
Ejemplos de coeficiente:
En el producto 3b el número 3 es el coeficiente del factor b, indicando que el factor b, se toma 3 veces como solución.
3b = b+b+b.
Si un producto es 9n, el factor “n” se tomará 9 veces.
9n = n+n+n+n+n+n+n+n+n+
9n = n+n+n+n+n+n+n+n+n+
En forma inversa, con los literales se toma así:
a4 = 4+4+4+4+4…a veces.
a4 = 4+4+4+4+4…a veces.
En el factor dc “d” es el coeficiente de c, por lo tanto.
dc = c+c+c+c+c….d veces.
dc = c+c+c+c+c….d veces.
En más de dos factores, los primeros son factores de los que le suceden.
En los factores opqr = “o” es el coeficiente de pqr; los factores op, son los coeficientes de qr; y opq son los factores de r.
En las cantidades que no tienen coeficiente numérico, el coeficiente se tendrá sobre entendido por defecto momo 1
En “n” se sobre entiende 1n; en “opqr” se sobre entiende 1opqr.
criterio de Eisenstein proporciona una condición suficiente para que un polinomio sea irreducible sobre el conjunto de los números racionales.
y un número primo  tal que
tal que
 tal que
tal que divide a todo
divide a todo  para i ≠ n
para i ≠ n no divide a
no divide a 
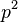 no divide a
no divide a 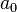
entonces  es irreducible sobre
es irreducible sobre ![\scriptstyle \mathbb{Q}[x]](https://upload.wikimedia.org/math/9/a/0/9a0e44f33b7891943944e2689f7bd78b.png) .
.
 es irreducible sobre
es irreducible sobre ![\scriptstyle \mathbb{Q}[x]](https://upload.wikimedia.org/math/9/a/0/9a0e44f33b7891943944e2689f7bd78b.png) .
.Ejemplos
Considérese  .
.
 .
.
Probaremos los siguientes primos  .
.
 .
.- p = 2
- 2 no divide a 15, entonces probaremos
- p = 3
- 3 no divide a 10, entonces probaremos
- p = 5
- 5 divide a 15, el coeficiente de x, y a 10, el término constante. Además, 5 no divide a 3, el primer coeficiente; y 25 = 52 no divide a 10. Concluiremos, por lo tanto, que g(x) es irreducible.
En algunos casos, la elección del primo puede ser poco clara, pero puede llegar a revelarse por un cambio de variable y = x + a. Por ejemplo, consideremos h(x) = x2 + x+ 2. Es aparentemente difícil, ya que ningún primo divide a 1, el coeficiente de x. Pero si cambiamos h(x) en h(x + 3) = x2 + 7x + 14 veremos inmediatamente que el primo 7 divide al coeficiente de x y al término constante, y que 49 no divide a 14. Así, con el cambio introducido, logramos que el polinomio satisficiera el criterio de Eisenstein.
Otro caso notable es el del polinomio ciclotómico para un primo p. Esto es:
(xp − 1)/(x − 1) = xp − 1 + xp − 2 + ... + x + 1.
Aquí, el polinomio satisface el criterio de Eisenstein, en una nueva variable y, después de establecer x = y + 1. El coeficiente constante será entonces p; los otros coeficientes son divisibles por p por las propiedades de los coeficientes binomiales C(p,k) que son p! dividido por algo que no involucra a p.
Prueba elemental
Considérese f(x) como un polinomio módulo p; esto es, redúzcanse los coeficientes al cuerpo Z/pZ. Entonces será c.xn para una constante c distinta de cero. Dado que dichos polinomios tienen una factorización única, cualquier factorización de f mod p resultará en monomios. Ahora, si f no fuese irreducible como polinomio entero, podríamos escribirlo como g.h, y f mod p como el producto de g mod p y h mod p. Estos últimos deben ser monomios, como acabamos de afirmar, por lo que tendremos que g mod p es d.xk y h mod p es e.xn-k donde c = d.e.
Vemos ahora que las condiciones dadas sobre g mod p y h mod p significan que p2 dividirá a a0, lo que contradice nuestra hipótesis. De hecho a0 será g(0).h(0) y pdivide a ambos factores, como hemos dicho más arriba.
Explicación avanzada
Aplicando la teoría del polígono de Newton para el campo de los números p-ádicos, para un polinomio de Eisenstein, se supone que tomaremos la menor envolturaconvexa de los puntos.
- (0,1), (1, v1), (2, v2), ..., (n − 1, vn-1), (n,0),
donde vi es la evaluación p-ádica de ai (es decir, la mayor potencia de p que lo divide). Ahora, los datos que tenemos sobre los vi for 0 < i < n, es decir, que existe por lo menos uno, es lo que necesitamos para concluir que la menor envoltura convexa es exactamente el único segmento de (0,1) a (n,0), con pendiente −1/n.
De la teoría general sabemos que p se ramifica completamente en la extensión de los números p-ádicos generados por una raíz de f. Por esa razón, f es irreducible sobre el campo p-ádico, y a fortiori sobre el campo de los números racionales.
Esta prueba es mucho más complicada que el argumento directo por reducción módulo p. Sin embargo, permite ver, en términos de teoría algebraica de números, la frecuencia con que puede aplicarse el criterio de Eisenstein después de algún cambio de variable; y así limita marcadamente la posible elección de p.
De hecho sólo los primos p que se ramifiquen en la extensión de Q generada por una raíz de f tienen alguna posibilidad de servir. Pueden ser hallados en términos deldiscriminante de f. Por ejemplo, en el caso de x2 + x + 2 dado más arriba, el discriminante es −7, de modo que 7 es el único primo con posibilidades de satisfacer el criterio. Se torna, mod 7, en:
- (x − 3)2
— es inevitable la repetición de una raíz, ya que el discriminante es 0 mod 7. Por lo tanto el cambio de variable es algo realmente predecible.
Una vez más, para el polinomio ciclotómico se torna en:
- (x − 1)p − 1 mod p;
Por métodos de álgebra lineal puede demostrarse que el discriminante es pp − 2 (excepto variación de signo).
Criterio de Eisenstein
Demostramos el criterio de Eisenstein y damos un ejemplo de aplicación.
Enunciado
(a) Demostrar el criterio de Eisenstein:
Sea Supongamos que existe primo tal que
Entonces, es irreducible en (como consecuencia también lo es en ).
(b) Demostrar que los polinomios y son irreducibles en
(a) Demostrar el criterio de Eisenstein:
Sea Supongamos que existe primo tal que
Entonces, es irreducible en (como consecuencia también lo es en ).
(b) Demostrar que los polinomios y son irreducibles en
Solución
(a) Por contradicción, si es reducible en por el lema de Gauss también es reducible en
(a) Por contradicción, si es reducible en por el lema de Gauss también es reducible en
(b) Para el polinomio elijamos Entonces,







No hay comentarios:
Publicar un comentario