FÍSICA - TEORÍA DE CUERDAS

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Cómo aparecería un vértice de tres gluones en la notación de doble índice de 't Hooft. Esto hace que la analogía con una teoría de cuerdas que aparecerá en N grande sea aparente.
Ejemplos
1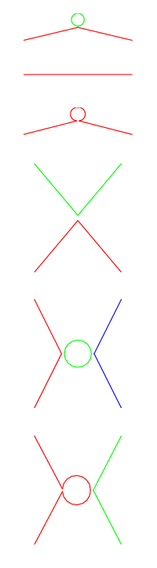	2

En la teoría de campo cuántica y la mecánica estadística , la 1 / N de expansión (también conocido como el " gran N" expansión ) es un particular, perturbative análisis de las teorías cuánticas de campo con una simetría interna grupotales como SO (N) o SU (N) . Consiste en derivar una expansión por las propiedades de la teoría en poderes de$${\ displaystyle 1 / N}, que se trata como un pequeño parámetro.

Esta técnica se utiliza en QCD (aunque$${\ displaystyle N}está solo 3 allí) con el grupo de indicadores SU (3). Otra aplicación en la física de partículas es el estudio de las dualidades de AdS / CFT .

También se utiliza ampliamente en la física de la materia condensada, donde se puede utilizar para proporcionar una base rigurosa para la teoría del campo medio .

Ejemplo [ editar ]

Comenzando con un ejemplo simple: la O (N) φ ⁴ - el campo escalar φ toma valores en la representación vectorial real de O (N). Usando la notación de índice para los N " sabores " con la convención de suma de Einstein y debido a que O (N) es ortogonal, no se hará distinción entre los índices covariantes y contravariantes. La densidad lagrangiana está dada por

$${\ displaystyle {\ mathcal {L}} = {1 \ sobre 2} \ parcial ^ {\ mu} \ phi _ {a} \ parcial _ {\ mu} \ phi _ {a} - {m ^ {2} \ over 2} \ phi _ {a} \ phi _ {a} - {\ lambda \ over 8N} (\ phi _ {a} \ phi _ {a}) ^ {2}}

dónde $${\ displaystyle a}corre de 1 a N. Tenga en cuenta que N ha sido absorbido por la fuerza de acoplamiento λ. Esto es crucial aquí.

Introduciendo un campo auxiliar F;

$${\ displaystyle {\ mathcal {L}} = {1 \ sobre 2} \ parcial ^ {\ mu} \ phi _ {a} \ parcial _ {\ mu} \ phi _ {a} - {m ^ {2} \ over 2} \ phi _ {a} \ phi _ {a} + {1 \ over 2} F ^ {2} - {{\ sqrt {\ lambda / N}} \ over 2} F \ phi _ {a } \ phi _ {a}}

En los diagramas de Feynman , el gráfico se divide en ciclos separados , cada uno compuesto por φ bordes del mismo sabor y los ciclos están conectados por F bordes.

Cada vértice de 4 puntos contribuye λ / N y, por tanto, 1 / N. Cada ciclo de sabor contribuye con N porque hay N tales sabores para resumir. Tenga en cuenta que no todos los ciclos de flujo de impulso son ciclos de sabor.

Al menos perturbativamente, la contribución dominante a la función de correlación conectada de 2k puntos es del orden (1 / N) ^k-1 y los otros términos son potencias superiores de 1 / N. Realizar una expansión 1 / N se vuelve cada vez más preciso en el gran límite de N. La densidad de energía de vacío es proporcional a N, pero puede ignorarse debido al incumplimiento de los supuestos de relatividad general.

Debido a esta estructura, se puede utilizar una notación gráfica diferente para indicar los diagramas de Feynman. Cada ciclo de sabor puede ser representado por un vértice. Las rutas de sabor que conectan dos vértices externos están representadas por un solo vértice. Los dos vértices externos a lo largo de la misma ruta de sabor están emparejados naturalmente y se pueden reemplazar por un solo vértice y un borde (no un borde F) que lo conecta a la ruta de sabor. Los bordes F son bordes que conectan dos ciclos / rutas de sabor entre sí (o un ciclo / ruta de sabor a sí mismo). Las interacciones a lo largo de un ciclo / ruta de sabor tienen un orden cíclico definido y representan un tipo especial de gráfico donde el orden de los bordes inciden en un vértice, pero solo hasta una permutación cíclica, y dado que esta es una teoría de los escalares reales, también una reversión de orden (pero si tenemos SU (N) en lugar de SU (2), las reversiones de orden no son " t valido). A cada borde F se le asigna un momento (la transferencia de momento) y hay una integral de momento interna asociada con cada ciclo de sabor.

QCD [ editar ]

Artículo principal: Cromodinámica cuántica.

QCD es una teoría de calibre SU (3) que involucra gluones y quarks . Los quarks zurdos pertenecen a una representación triplete , los diestros a una representación antitriplet (después de conjugarlos) y los gluones a una representación adjunta real . A un borde de quark se le asigna un color y una orientación y a un borde de gluón se le asigna un par de colores.

En el gran límite de N, solo consideramos el término dominante. Ver AdS / CFT .

En física teórica, la teoría de campos superconformales de seis dimensiones (2,0) es una teoría de campos cuántica cuya existencia se predice con argumentos en la teoría de cuerdas . Todavía se entiende poco porque no hay una descripción conocida de la teoría en términos de una acción funcional . A pesar de la dificultad inherente en el estudio de esta teoría, se considera un objeto interesante por una variedad de razones, tanto físicas como matemáticas.

Aplicaciones [ editar ]

La teoría (2.0) ha demostrado ser importante para estudiar las propiedades generales de las teorías de campos cuánticos. De hecho, esta teoría incluye una gran cantidad de teorías de campo cuántico efectivas matemáticamente interesantes y apunta a nuevas dualidades que relacionan estas teorías. Por ejemplo, Luis Alday, Davide Gaiotto y Yuji Tachikawa demostraron que al compactar esta teoría en una superficie , se obtiene una teoría del campo cuántico de cuatro dimensiones, y existe una dualidadconocida como la correspondencia AGT que relaciona la física de esta teoría con Ciertos conceptos físicos asociados a la superficie misma. ^[2]Más recientemente, los teóricos han extendido estas ideas para estudiar las teorías obtenidas al compactar hasta tres dimensiones. ^[3]

Además de sus aplicaciones en la teoría cuántica de campos, la teoría (2.0) ha generado una serie de resultados importantes en matemáticas puras . Por ejemplo, la existencia de la teoría (2.0) fue utilizada por Witten para dar una explicación "física" de una relación conjetural en matemáticas llamada correspondencia geométrica de Langland . ^[4] En un trabajo posterior, Witten demostró que la teoría (2.0) podría usarse para comprender un concepto en matemáticas llamado homología de Khovanov . ^[5] Desarrollado por Mikhail Khovanov hacia el año 2000, la homología de Khovanov proporciona una herramienta en la teoría de nudos., la rama de las matemáticas que estudia y clasifica las diferentes formas de los nudos. ^[6] Otra aplicación de la teoría (2.0) en matemáticas es el trabajo de Davide Gaiotto, Greg Moore y Andrew Neitzke, que utilizó ideas físicas para derivar nuevos resultados en la geometría hiperkähler .

 la teoría ABJM es una teoría cuántica de camposestudiada por Ofer Aharony, Oren Bergman, Daniel Jafferis y Juan Maldacena . Proporciona un dual holográfico a la teoría M sobre$${\ displaystyle AdS_ {4} \ times S ^ {7}}. La teoría ABJM también está estrechamente relacionada con la teoría de Chern-Simons , y sirve como un modelo de juguete útil para resolver problemas que surgen en la física de la materia condensada.