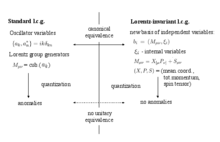
Por lo general , la teoría de cuerdas no crítica se considera en marcos del enfoque propuesto por Polyakov . [1] El otro enfoque se ha desarrollado en [2] [3] . [4] Representa un método universal para mantener la invarianciaexplícita de Lorentz en cualquier teoría relativista cuántica. En un ejemplo de la teoría de cuerdas Nambu-Gotoen el espacio-tiempo Minkowski 4-dimensional , la idea se puede demostrar de la siguiente manera:
Geométricamente, la hoja de cuerdas del mundo está cortada por un sistema de planos paralelos para arreglar una parametrización específica, o calibrarla . Los planos están definidos por un vector normal n μ , el eje de medición. Si este vector pertenece al cono de luz , la parametrización corresponde al calibre de cono de luz , si se dirige a lo largo del periodo P μ de la lámina de mundo , es el calibre de Rohrlich similar al tiempo . El problema del medidor de cono de luz estándar es que el vector n μ es constante, por ejemplo, n μ = (1, 1, 0, 0), y el sistema de planos está "congelado" en el espacio-tiempo de Minkowski.Las transformaciones de Lorentz cambian la posición de la hoja mundial con respecto a estos planos fijos, y son seguidas por reparametrizaciones de la hoja mundial. En el nivel cuántico, el grupo de reparametrización tiene una anomalía , que aparece también en el grupo de Lorentz y viola la invariancia de la teoría de Lorentz . Por otro lado, el indicador de Rohrlich se relaciona n μcon la propia hoja del mundo. Como resultado, los generadores de Lorentz transforman n μ y la hoja mundial simultáneamente, sin reparametrizaciones. La misma propiedad es válida si uno relaciona el eje similar a la luz n μ con la hoja del mundo, usando además de P μOtros vectores dinámicos disponibles en la teoría de cuerdas. De esta manera, se construye la parametrización invariante de Lorentz de la hoja del mundo, donde el grupo de Lorentz actúa de forma trivial y no tiene anomalías cuánticas.
Algebraicamente esto corresponde a una transformación canónica a i -> b i en la mecánica clásica a un nuevo conjunto de variables, que contiene explícitamente todos los generadores necesarios de simetrías. Para el medidor de cono de luz estándar, los generadores de Lorentz M μν son cúbicos en términos de variables del oscilador a i , y su cuantificación adquiere una anomalía bien conocida. Considere un conjunto b i = (M μν , ξ i ) que contiene los generadores del grupo de Lorentz y las variables internas ξ i , que complementan M μν al espacio de fase completo. En la selección de un conjunto de este tipo, hay que tener cuidado de queitendrá simples paréntesis de Poisson con M μν y entre sí. La existencia local de tales variables es proporcionada por el teorema de Darboux . La cuantización en el nuevo conjunto de variables elimina la anomalía del grupo de Lorentz. Las teorías clásicas canónicamente equivalentes no se corresponden necesariamente con las teorías cuánticas de unidades equivalentes , por eso las anomalías cuánticas pueden estar presentes en un enfoque y ausentes en el otro.
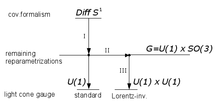
En teoría, la teoría de cuerdas de grupo tiene una simetría gauge Diff S 1 , reparametrizaciones de un círculo. La simetría es generada por elálgebra de Virasoro L n . El medidor de cono de luz estándar fija la mayor parte de los grados de libertad del medidor, dejando solo rotaciones de fase trivial U (1) ~ S 1 . Corresponden a la evolución periódica de la cadena, generada por Hamiltonian L 0 . Introduzcamos una capa adicional en este diagrama: un grupo G = U (1) x SO (3) de transformaciones de calibre de la hoja mundial, que incluyen el factor de evolución trivial y las rotaciones del eje del calibre en el marco del centro de masa, con respecto a la hoja fija mundial. El medidor de cono de luz estándar corresponde a una selección de un punto en el factor SO (3), lo que lleva a la parametrización no invariante de Lorentz. Por lo tanto, uno debe seleccionar un representante diferente en la órbita de G, esta vez relacionada con la hoja mundial de manera invariante de Lorentz. Después de la reducción de la mecánica a este indicador anómalo, los grados de libertad se eliminan de la teoría. La simetría de calibre trivial U (1) x U (1) permanece, incluidas la evolución y las rotaciones que conservan la dirección del eje del calibre.
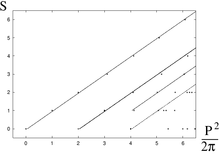
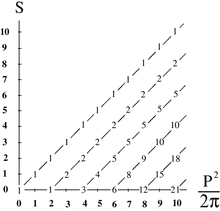
La implementación exitosa de este programa se ha realizado en [3] [4] . [5]Estas son varias versiones unitarias no equivalentes de la teoría cuántica de cuerdas abiertas de Nambu-Goto, donde el eje de calibre está unido a diferentes características geométricas de la hoja del mundo. Sus propiedades comunes son.
- Lorentz-invarianza explícita en d = 4
- Grados de reparación reparametrización fijados por el ancho de vía.
- Regge-como espectro de spin-masa
El lector familiarizado con la variedad de ramas que coexisten en la moderna teoría de cuerdas no se preguntará por qué se pueden construir muchas teorías cuánticas diferentes para esencialmente el mismo sistema físico. El enfoque descrito aquí no tiene la intención de producir un resultado final único, solo proporciona un conjunto de herramientas adecuadas para la construcción de su propia teoría cuántica de cuerdas. Dado que se puede usar cualquier valor de dimensión, y especialmente d = 4, las aplicaciones podrían ser más realistas. Por ejemplo, el enfoque puede aplicarse en la física de los hadrones , para describir sus espectros e interacciones electromagnéticas.
La teoría M es una teoría de la física que unifica todas las versiones coherentes de la teoría de supercuerdas . La existencia de tal teoría fue conjeturada por primera vez por Edward Witten en una conferencia de teoría de cuerdas en la Universidad del Sur de California en la primavera de 1995. El anuncio de Witten inició una serie de actividades de investigación conocidas como la segunda revolución de supercuerdas .
Antes del anuncio de Witten, los teóricos de cuerdas habían identificado cinco versiones de la teoría de supercuerdas. Aunque estas teorías parecían, al principio, ser muy diferentes, el trabajo de varios físicos demostró que las teorías estaban relacionadas de manera intrincada y no trivial. En particular, los físicos descubrieron que aparentemente distintas teorías podrían ser unificadas por las transformaciones matemáticas llamadas S-dualidad y la T-dualidad. La conjetura de Witten se basó en parte en la existencia de estas dualidades y en parte en la relación de las teorías de cuerdas con una teoría de campo llamada supergravedad de once dimensiones .
Aunque no se conoce una formulación completa de la teoría M, la teoría debería describir objetos de dos y cinco dimensiones denominados branas y debería aproximarse a la supergravedad de once dimensiones a bajas energías . Los intentos modernos de formular la teoría M se basan típicamente en la teoría de matrices o la correspondencia AdS / CFT .
Según Witten, M debe significar "magia", "misterio" o "membrana" según el gusto, y el verdadero significado del título debe decidirse cuando se conoce una formulación más fundamental de la teoría. [1]
Las investigaciones de la estructura matemática de la teoría M han generado importantes resultados teóricos en física y matemáticas. Más especulativamente, la teoría M puede proporcionar un marco para desarrollar una teoría unificada de todas las fuerzas fundamentales de la naturaleza. Los intentos de conectar la teoría M para experimentar normalmente se centran en la compactación de sus dimensiones adicionales para construir modelos candidatos de nuestro mundo cuatridimensional, aunque hasta ahora no se ha verificado que ninguno de ellos genere la física como se observa en experimentos de física de alta energía.
Fondo [ editar ]
La gravedad cuántica y cuerdas [ editar ]
Uno de los problemas más profundos en la física moderna es el problema de la gravedad cuántica . La comprensión actual de la gravedad se basa en Albert Einstein 's teoría general de la relatividad , que se formula en el marco de la física clásica . Sin embargo, las fuerzas no gravitacionales se describen en el marco de la mecánica cuántica , un formalismo radicalmente diferente para describir fenómenos físicos basados en la probabilidad . [a] Se necesita una teoría cuántica de la gravedad para reconciliar la relatividad general con los principios de la mecánica cuántica, [b]pero surgen dificultades cuando uno intenta aplicar las prescripciones habituales de la teoría cuántica a la fuerza de la gravedad. [do]
La teoría de cuerdas es un marco teórico que intenta reconciliar la gravedad y la mecánica cuántica. En la teoría de cuerdas, las partículas puntuales de la física de partículas son reemplazadas por objetos unidimensionalesllamados cadenas . La teoría de cuerdas describe cómo las cadenas se propagan a través del espacio e interactúan entre sí. En una versión dada de la teoría de cuerdas, solo hay un tipo de cadena, que puede parecer un pequeño bucle o segmento de cadena ordinaria, y puede vibrar de diferentes maneras. En escalas de distancia más grandes que la escala de cuerda, una cuerda se verá como una partícula ordinaria, con su masa , carga, y otras propiedades determinadas por el estado vibracional de la cadena. De esta manera, todas las diferentes partículas elementales pueden verse como cuerdas vibrantes. Uno de los estados vibracionales de una cuerda da origen al gravitón , una partícula mecánica cuántica que transporta la fuerza gravitacional. [re]
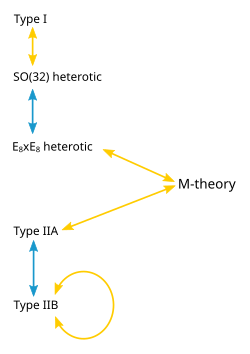
Existen varias versiones de la teoría de cuerdas: tipo I , tipo IIA , tipo IIB y dos tipos de teoría heterótica de cuerdas ( SO (32) y E 8 × E 8 ). Las diferentes teorías permiten diferentes tipos de cuerdas, y las partículas que surgen a bajas energías exhiben simetrías diferentes . Por ejemplo, la teoría del tipo I incluye tanto cadenas abiertas (que son segmentos con puntos finales) como cadenas cerradas (que forman bucles cerrados), mientras que los tipos IIA y IIB incluyen solo cadenas cerradas. [2]Cada una de estas cinco teorías de cuerdas surge como un caso limitante especial de la teoría M. Esta teoría, al igual que sus antecesores de la teoría de cuerdas, es un ejemplo de una teoría cuántica de la gravedad. Describe una fuerza como la fuerza gravitacional familiar sujeta a las reglas de la mecánica cuántica. [3]
Número de dimensiones [ editar ]
En la vida cotidiana, hay tres dimensiones familiares del espacio: altura, anchura y profundidad. La teoría general de la relatividad de Einstein trata el tiempo como una dimensión a la par con las tres dimensiones espaciales; en general, la relatividad, el espacio y el tiempo no se modelan como entidades separadas, sino que se unifican en un espacio- tiempo de cuatro dimensiones , tres dimensiones espaciales y una dimensión temporal. En este marco, el fenómeno de la gravedad se ve como una consecuencia de la geometría del espacio-tiempo. [4]
A pesar del hecho de que el universo está bien descrito por el espacio-tiempo de cuatro dimensiones, hay varias razones por las cuales los físicos consideran las teorías en otras dimensiones. En algunos casos, al modelar el espacio-tiempo en un número diferente de dimensiones, una teoría se vuelve más manejable matemáticamente, y uno puede realizar cálculos y obtener información general más fácilmente. [e] También hay situaciones en las que las teorías en dos o tres dimensiones del espacio-tiempo son útiles para describir fenómenos en la física de la materia condensada . [5] Finalmente, existen escenarios en los que podría haber más de cuatro dimensiones del espacio-tiempo que, sin embargo, han logrado escapar de la detección. [6]
Una característica notable de la teoría de cuerdas y la teoría M es que estas teorías requieren dimensiones adicionales de espacio-tiempo para su consistencia matemática. En la teoría de cuerdas, el espacio - tiempo es de diez dimensiones (nueve dimensiones espaciales y una dimensión de tiempo),mientras que en la teoría M es de once dimensiones (diez dimensiones espaciales y una dimensión temporal). Para describir los fenómenos físicos reales utilizando estas teorías, uno debe, por lo tanto, imaginar escenarios en los que estas dimensiones adicionales no se observen en los experimentos. [7]
La compactación es una forma de modificar el número de dimensiones en una teoría física. [f] En la compactificación, se supone que algunas de las dimensiones adicionales se "cierran" sobre sí mismas para formar círculos. [8] En el límite donde estas dimensiones curvadas se vuelven muy pequeñas, se obtiene una teoría en la que el espacio-tiempo tiene efectivamente un número menor de dimensiones. Una analogía estándar para esto es considerar un objeto multidimensional como una manguera de jardín. Si se ve la manguera desde una distancia suficiente, parece tener solo una dimensión, su longitud. Sin embargo, a medida que uno se acerca a la manguera, uno descubre que contiene una segunda dimensión, su circunferencia. Por lo tanto, una hormiga que se arrastra en la superficie de la manguera se movería en dos dimensiones. [sol]
Dualidades [ editar ]
Las teorías que surgen como límites diferentes de la teoría M se relacionan de manera no trivial. Una de las relaciones que pueden existir entre estas diferentes teorías físicas se llama dualidad-S . Esta es una relación que dice que una colección de partículas que interactúan fuertemente en una teoría puede, en algunos casos, verse como una colección de partículas que interactúan débilmente en una teoría completamente diferente. En términos generales, se dice que una colección de partículas interactúa fuertemente si se combinan y se descomponen con frecuencia y de interacción débil si lo hacen con poca frecuencia. La teoría de cuerdas de tipo I resulta ser equivalente por dualidad S a la teoría de cuerdas heterótica SO (32) . De manera similar, la teoría de cuerdas de tipo IIB se relaciona consigo misma de una manera no trivial por la dualidad S.[10]
Otra relación entre las diferentes teorías de cuerdas es T-dualidad . Aquí se consideran cuerdas que se propagan alrededor de una dimensión extra circular. La dualidad T indica que una cadena que se propaga alrededor de un círculo de radio R es equivalente a una cadena que se propaga alrededor de un círculo de radio 1 / R en el sentido de que todas las cantidades observables en una descripción se identifican con cantidades en la descripción dual. Por ejemplo, una cuerda tiene impulso a medida que se propaga alrededor de un círculo, y también puede enrollarse alrededor del círculo una o más veces. La cantidad de veces que la cuerda se enrolla alrededor de un círculo se denomina número de cuerda . Si una cuerda tiene impulso p y número de giro nen una descripción, tendrá un impulso n y un número de giro p en la descripción dual. Por ejemplo, la teoría de cuerdas de tipo IIA es equivalente a la teoría de cuerdas de tipo IIB a través de la dualidad T, y las dos versiones de la teoría de cuerdas heterótica también están relacionadas por la dualidad T. [10]
En general, el término dualidad se refiere a una situación en la que dos sistemas físicos aparentemente diferentes resultan ser equivalentes de una manera no trivial. Si dos teorías están relacionadas por una dualidad, significa que una teoría puede transformarse de alguna manera para que termine pareciéndose a la otra teoría. Luego se dice que las dos teorías son duales entre sí durante la transformación. En otras palabras, las dos teorías son descripciones matemáticamente diferentes de los mismos fenómenos. [11]
Supersimetria [ editar ]
Otra idea teórica importante que juega un papel en la teoría M es la supersimetría . Esta es una relación matemática que existe en ciertas teorías físicas entre una clase de partículas llamadas bosones y una clase de partículas llamadas fermiones . En términos generales, los fermiones son los constituyentes de la materia, mientras que los bosones median las interacciones entre las partículas. En las teorías con supersimetría, cada bosón tiene una contraparte que es un fermión, y viceversa. Cuando la supersimetría se impone como una simetría local, uno obtiene automáticamente una teoría cuántica mecánica que incluye la gravedad. Tal teoría se llama teoría de supergravedad . [12]
Una teoría de cuerdas que incorpora la idea de supersimetría se llama teoría de supercuerdas . Hay varias versiones diferentes de la teoría de supercuerdas que están incluidas en el marco de la teoría M. A bajas energías , las teorías de supercuerdas se aproximan a la supergravedad en diez dimensiones de espacio-tiempo. De manera similar, la teoría M se aproxima a bajas energías por la supergravedad en once dimensiones. [3]
Branes [ editar ]
En la teoría de cuerdas y teorías relacionadas, como las teorías de supergravedad, una brana es un objeto físico que generaliza la noción de partícula puntual a dimensiones más altas. Por ejemplo, una partícula puntual puede verse como una brana de dimensión cero, mientras que una cuerda puede verse como una brana de dimensión uno. También es posible considerar branas de dimensión superior. En la dimensión p , estos se llaman p -branes. Las branas son objetos dinámicos que pueden propagarse a través del espacio-tiempo de acuerdo con las reglas de la mecánica cuántica. Pueden tener masa y otros atributos como carga. Una p- grúa barre un volumen tridimensional ( p + 1) en el espacio-tiempo llamado su volumen mundial. Los físicos a menudo estudian camposanálogos al campo electromagnético que vive en el volumen mundial de una brana. La palabra brana proviene de la palabra "membrana" que se refiere a una brana bidimensional. [13]
En la teoría de cuerdas, los objetos fundamentales que dan origen a partículas elementales son las cuerdas unidimensionales. Aunque los fenómenos físicos descritos por la teoría M aún no se conocen bien, los físicos saben que la teoría describe branas bidimensionales y cinco dimensiones. Gran parte de la investigación actual en la teoría M intenta comprender mejor las propiedades de estas branas. [h]
Historia y desarrollo [ editar ]
Teoría Kaluza-Klein [ editar ]
A principios del siglo XX, los físicos y matemáticos, incluidos Albert Einstein y Hermann Minkowski, fueron pioneros en el uso de la geometría de cuatro dimensiones para describir el mundo físico. [14] Estos esfuerzos culminaron en la formulación de la teoría general de la relatividad de Einstein, que relaciona la gravedad con la geometría del espacio-tiempo de cuatro dimensiones. [15]
El éxito de la relatividad general llevó a los esfuerzos para aplicar geometría dimensional superior para explicar otras fuerzas. En 1919, el trabajo de Theodor Kaluza demostró que al pasar al espacio-tiempo de cinco dimensiones, uno puede unificar la gravedad y el electromagnetismo en una sola fuerza. [15] Esta idea fue mejorada por el físico Oskar Klein , quien sugirió que la dimensión adicional propuesta por Kaluza podría tomar la forma de un círculo con un radio de alrededor de 10 a 30 cm. [dieciséis]
La teoría de Kaluza-Klein y los intentos posteriores de Einstein para desarrollar una teoría de campo unificadanunca fueron completamente exitosos. En parte esto fue porque la teoría de Kaluza-Klein predijo una partícula [ ¿cuál? ] que nunca se ha demostrado que exista, y en parte porque no pudo predecir correctamente la relación entre la masa de un electrón y su carga. Además, estas teorías se estaban desarrollando justo cuando otros físicos comenzaban a descubrir la mecánica cuántica, lo que finalmente resultaría exitoso al describir fuerzas conocidas como el electromagnetismo, así como nuevas fuerzas nucleares.que fueron descubiertos a mediados del siglo. Por lo tanto, tomaría casi cincuenta años para que la idea de nuevas dimensiones se tome en serio nuevamente.




No hay comentarios:
Publicar un comentario