Electrónica: conceptos, definiciones, leyes, teoremas

Tensión eléctrica. Diferencia de potencial

Es la diferencia de potencia eléctrico provocado por la acumulación de cargas en un punto o en un material.

Si un material se le quitan electrones, su carga eléctrica total será positiva. Ver el primer diagrama.

Hay que recordar que se le está quitando a un átomo neutro (no tiene carga), electrones que tienen carga negativa. Esto causa que el átomo ya no sea neutro sino que tenga carga positiva.

Ver que en este caso hay en el átomo 6 protones (carga positiva) y 4 electrones (carga negativa). En conclusión la carga total es positiva.

Si ahora al material se aumentan electrones (tiene ahora más de los que tiene cuando el átomo es neutro), su carga total será negativa. Ver el segundo diagrama.

Ver que en este caso hay en el átomo 6 protones (carga positiva) y 8 electrones(carga negativa). En conclusión la carga total es negativa.

Si se tienen dos materiales con diferentes niveles o tipos de carga, se dice entonces que hay una diferencia de potencial entre ellos.

Para poder lograr cargar de alguna manera los materiales, es necesario aplicar energía al átomo.

Hay varios métodos para lograrlo:

- por frotamiento
- por presión
- por calor
- por magnetismo
- por una acción química

La unidad en que se mide la diferencia de potencial es el voltio (V).

RELACIÓN ENTRE CAMPO Y POTENCIAL   Después de ver el campo, E, y el potencial, V, son dos formas distintas de caracterizar el campo eléctrico, interesa fijarse en la relación entre ambos conceptos. La relación matemática entre ambos conceptos se expresa diciendo que el campo es igual al gradiente (negativo) del potencial, y esto, limitando el análisis a una sola componente espacial, x, se reduce a:     Expresión que supone que la magnitud de la componente del campo eléctrico en la dirección adoptada, x, equivale al ritmo de variación del potencial eléctrico con la distancia. El signo menos indica que la orientación del campo es la que coincide con el sentido hacia el que el potencial decrece.     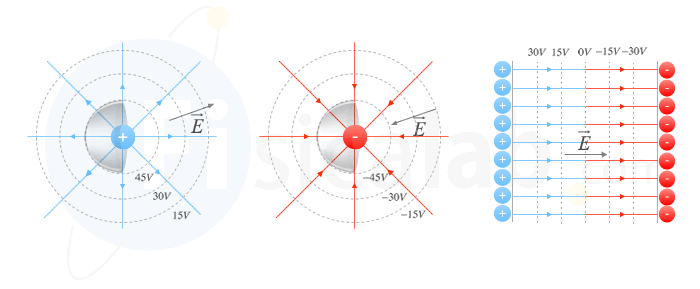En la figura de la izquierda se visualiza esta relación en el caso del campo creado por una carga puntual de signo positivo. En este caso, las líneas de fuerza del campo eléctrico forman un haz que emerge de la carga en todas las direcciones y se dirige hacia el exterior. Junto con ellas, se han dibujado también tres superficies esféricas (1, 2 y 3) con centro en la carga. Son superficies equipotenciales, ya que, como el valor del potencial eléctrico depende únicamente de la carga y de la distancia, en todos los puntos que pertenecen a cada una de estas superficies, el potencial tiene un valor constante. El dibujo completo muestra que, tal como predice la relación escrita un poco más arriba, las líneas del campo eléctrico atraviesan a dichas superficies equipotenciales perpendicularmente y se dirigen desde donde el potencial el mayor (superficie 1) hacia donde es menor (superficie 3).   Este tipo de representación, que dibuja las líneas de fuerza del campo y superficies equipotenciales, es muy instructivo, porque, después de calcular el potencial el cada punto circundante a cualquier distribución de carga, ayuda a prever la dirección y el sentido de las líneas de fuerza del campo, y viceversa. Como ejemplo, se muestran a la derecha las líneas del campo eléctrico (en color rojo) y las superficies equipotenciales (en azul) de un dipolo eléctrico, formado por dos cargas puntuales de signos opuestos (la positiva representada de color rojo y la negativa de color verde).       Un caso de especial interés es el condensador plano. Entre sus placas el campo eléctrico es prácticamente uniforme y por eso sus líneas de fuerza son casi paralelas. Dichas líneas se dirigen desde la zona donde el potencial el mayor (la placa con carga positiva) hacia donde es menor (la placa con carga negativa). A su camino atraviesan las superficies equipotenciales, en este caso planos paralelos a las placas, siendo mayor el potencial cuanto más cerca se esté de la placa positiva (superficie 1) y menor cuanto más cerca ese esté de la negativa (superficie 3).   En este caso especial, la intensidad del campo eléctrico uniforme existente entre las placas y la tensión, V, o diferencia de potencial entre ellas, se relacionan mediante la sencilla expresión:     En este documento se deducen, mediante desarrollos sencillos, las dos expresiones que aparecen en esta página. Quienes estén interesados, pueden consultar en este otro documento el desarrollo de la relación entre el campo y el potencial eléctrico creados por una carga puntual, considerando las tres dimensiones del espacio. Si introducimos una carga q' en el seno de un campo eléctrico, la carga sufrirá la acción de una fuerza eléctrica y como consecuencia de esto, adquirirá cierta energía potencial eléctrica (también conocida como energía potencial electrostática). Si lo vemos desde una perspectiva más simple, podemos pensar que el campo eléctrico crea un área de influencia donde cada uno de sus puntos tienen la propiedad de poder conferir una energía potencial a cualquier carga que se sitúe en su interior. A partir de este razonamiento, se establece una nueva magnitud escalar propia de los campos eléctricos denominadapotencial eléctrico y que representa la energía potencial electrostática que adquiere una unidad de carga positiva si la situamos en dicho punto. El potencial eléctrico en un punto del espacio de un campo eléctrico es la energía potencial eléctrica que adquiere una unidad de carga positiva situada en dicho punto. V=Epq' donde: V es el potencial eléctrico en un punto del campo eléctrico. Su unidad en el S.I. es el julio por culombio (J/C) que en honor a Alesandro Volta recibe el nombre de Voltio. Ep es la energía potencial eléctrica que adquiere una carga testigo positiva q' al situarla en ese punto. El hecho de que todas las magnitudes sean escalares, permite que el estudio del campo eléctrico sea más sencillo. De esta forma, si conocemos el valor del potencial eléctrico V en un punto, podemos determinar que la energía potencial eléctrica de una carga q situada en él es: Ep=V⋅q Potencial eléctrico creado por una carga puntual Tal y como estudiamos en el apartado de intensidad del campo eléctrico, una única carga q es capaz de crear un campo eléctrico a su alrededor. Si en dicho campo introducimos una carga testigo q' entonces, atendiendo a la definición de energía potencial eléctrica de dos cargas puntuales: V=Epq'=K⋅q⋅q'rq'⇒V=K⋅qr El potencial eléctrico del campo eléctrico creado por una carga puntual q se obtiene por medio de la siguiente expresión: V=K⋅qr donde: V es el potencial eléctrico en un punto. K es la constante de la ley de Coulomb. q es la carga puntual que crea el campo eléctrico. r es la distancia entre la carga y el punto donde medimos el potencial. Si observas detenidamente la expresión puedes darte cuenta de que: Si la carga q es positiva, la energia potencial es positiva y el potencial eléctrico V es positivo. Si la carga q es negativa, la energía el potencial es negativa y el potencial eléctrico V es negativo. Si no existe carga, la energía potencial y el potencial eléctrico es nulo. El potencial eléctrico no depende de la carga testigo q' que introducimos para medirlo. Ejemplo ¿Cuál es el potencial eléctrico creado por una carga puntual de -2 mC en un punto situado a 5 metros de ella en el vacío? Ver solución Potencial eléctrico creado por varias cargas puntuales Si el campo eléctrico es creado por varias cargas puntuales, el potencial eléctrico en un punto sigue el principio de superposición: El potencial eléctrico originado por n cargas puntuales en un punto de un campo eléctrico es la suma escalar de los potenciales eléctricos en dicho punto creados por cada una de las cargas por separado. V=V1+V2+...+Vn=∑i=1nVi o lo que es lo mismo: V=K⋅(q1r1+q2r2+...+qnrn)=K⋅∑i=1nqiri Diferencia de Potencial Eléctrico Si dos puntos de un campo eléctrico poseen distinto potencial eléctrico, entre ambos puntos existe lo que se denomina unadiferencia de potencial o tensión, ΔV. Este valor se encuentra íntimamente relacionado con el trabajo eléctrico. Por definición, el trabajo que debe realizar un campo eléctrico para trasladar una carga q desde un punto A a otro B dentro del campo se obtiene por medio de la siguiente expresión: We(A→B)=−(EpB − EpA) = EpA − EpB Si aplicamos la definición de potencial eléctrico, obtenemos que: We(A→B)=EpA−EpB=q⋅VA−q⋅VB = q⋅(VA−VB) La diferencia de potencial eléctrico entre dos puntos A y B de un campo eléctrico es el opuesto del trabajo realizado por el campo eléctrico para trasladar una unidad de carga positiva desde el punto A al B. ∆V=VB−VA=−We(A→B)q Potencial Eléctrico y el Movimiento de las Cargas Si analizamos detenidamente la expresión de la diferencia de potencial: VB−VA=−We(A→B)q Tal y como vimos en el apartado del trabajo eléctrico, el trabajo realizado por una fuerza eléctrica para desplazar una carga qdesde un punto A a otro B, sin presencia de fuerzas externas, es un valor positivo. Si estudiamos que ocurre si la carga q es positiva o negativa, obtenemos que: q < 0 VB-VA >0 => VB>VA La carga se mueve desde puntos de menor potencial a mayor potencial q > 0 VB-VA<0> VBA

Se mueve desde puntos de mayor potencial a menor potencial

Por tanto:

• Las cargas positivas se mueven desde zonas de mayor potencial eléctrico a zonas de menor potencial eléctrico.
• Las cargas negativas se mueven desde zonas de menor potencial eléctrico a zonas de mayor potencial eléctrico.

Teniendo en cuenta que tal y como estudiamos en el apartado de intensidad del campo eléctrico, las cargas positivas se mueven en el sentido de dicha intensidad entonces, la intensidad de campo eléctrico se dirige siempre desde zonas de mayor potencial a zonas de menor potencial.

La intensidad de campo eléctrico apunta siempre hacia potenciales decrecientes.