Física - Mecánica clásica

Astrodinámica

semieje mayor de una elipse es la mitad del diámetro más largo; su símbolo es a. En astronomía, es equivalente a la distancia media de un objeto que orbita alrededor de otro, ya que el objeto central (por ejemplo, el Sol) ocupa uno de los focos.

Parámetros de una elipse. El semieje mayor está representado aquí por a, que corresponde a la misma distancia entre el centro de la elipse y los puntos A y B, es decir, la mitad del eje mayor.

El semieje mayor es una de las características más importantes de una órbita, junto con su período orbital. Puede ser matemáticamente probado que para un cuerpo orbitando, el semieje mayor representa la distancia media del cuerpo a la fuente central gravitacional. Para los objetos del Sistema Solar, el semieje mayor está relacionado con el período de la órbita por la tercera ley de Kepler, originalmente descrita como:

${\displaystyle P^{2}=ka^{3}\,}$

donde P es el período medido en años, a es el semieje mayor medido en unidades astronómicas y k una constante de proporcionalidad.

Esta fórmula fue modificada por Newton al desarrollar su teoría gravitatoria, expresándola como:

${\displaystyle P^{2}={\frac {4\pi ^{2}}{GM}}a^{3}}$

donde G es la Constante de gravitación universal y M es la masa del cuerpo central.

semieje menor de una elipse es la mitad del diámetro más corto; su símbolo es b.

De la definición de elipse, el extremo del eje menor equidista de los focos y dichas distancias (F₁-C y F₂-C) equivalen a la medida del semieje mayor a.

El centro de la elipse, el foco y el extremo del semieje menor conforman un triángulo rectángulo. Aplicando el Teorema de Pitágoras:

${\displaystyle a^{2}=b^{2}+c^{2}\,}$

donde c es la semi-distancia focal.

Como la excentricidad es: ${\displaystyle e={\frac {c}{a}}}$, su relación será:

${\displaystyle b=a\cdot {\sqrt {1-e^{2}}}}$

${\displaystyle b^{2}=al\,\!}$

donde (ℓ) es el semi-latus rectum de una elipse.

Parámetros de una elipse. El semieje menor: b

Semi-latus rectum (ℓ) de una elipse.

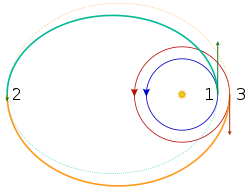
La transferencia bielíptica es una maniobra orbital que traslada una nave espacial desde una órbita hacia otra y que, en algunas situaciones, requiere un menor cambio en la velocidad que una transferencia de Hohmann, lo que se traduce en un menor gasto de combustible.

La transferencia bielíptica consiste en dos medias órbitas elípticas. Desde una órbita inicial, un primer encendido de motor brinda un delta-v para impulsar al vehículo hacia una órbita elípica exterior. En el apoapsis de esta órbita elíptica, un segundo encendido de motor envía al vehículo a una segunda órbita elíptica, cuya periapsis coincide con el radio de la órbita final. En este punto, un tercer encendido de motor desacelera el vehículo de modo que este queda confinado a la órbita final que se deseaba alcanzar.

Transferencia bielíptica desde una órbita circular baja (azul) a una órbita circular más alta (rojo).

Una trayectoria terrestre (del inglés ground track) es el camino en la superficie de la Tierra directamente debajo de una aeronave o satélite. En el caso de un satélite, es la proyección de la órbita del satélite sobre la superficie de la Tierra (o del cuerpo en el que el satélite está orbitando).

Una trayectoria terrestre de satélite puede ser pensada como un camino a lo largo de la superficie terrestre que traza el movimiento de una línea imaginaria entre el satélite y el centro de la tierra. En otras palabras, la trayectoria terrestre es el conjunto de puntos por los cuales el satélite pasará directamente arriba, o cruza el cenit, en el marco de referencia de un observador de la Tierra.

Trayectoria terrestre de la Estación espacial internacional. Las regiones claras y oscuras representan el día y la noche.

La velocidad de escape es la velocidad mínima con la que debe lanzarse un cuerpo para que escape de la atracción gravitatoria de la Tierra o de cualquier otro astro. Por tratarse de la velocidad mínima, la velocidad final del cuerpo será nula. Esto significa que el cuerpo o proyectil no volverá a caer sobre la Tierra o astro de partida, quedando en reposo a una distancia suficientemente grande (en principio, infinita) de la Tierra o del astro.

Ilustración del razonamiento de Isaac Newton. Desde la Cima de una montaña, un cañón dispara proyectiles con cada vez más velocidad. Los proyectiles A y B caen en tierra. El proyectil C entra en órbita circular y el D en órbita elíptica. El proyectil E se libera de la atracción terrestre.

Concepto

La velocidad de escape es aplicable tan solo a objetos que dependan únicamente de su impulso inicial (proyectiles) para vencer la atracción gravitatoria; no es aplicable a los cohetes, lanzaderas espaciales u otros artefactos con propulsión propia.

La velocidad de escape depende de la forma del potencial gravitatorio en que se encuentra el proyectil, por lo que el planteamiento sería ligeramente distinto si el punto de partida está situado en el interior o en el exterior del astro. En el exterior del astro, sobre la superficie de éste, la velocidad de escape depende solamente de la altura del punto de lanzamiento, si se desprecian las fuerzas de fricción en la atmósfera, si la hubiere (como es el caso de la Tierra).

La velocidad de escape no depende de la masa del proyectil; tampoco depende de la dirección del lanzamiento, como se verá luego en su deducción en términos puramente energéticos.

La velocidad de escape desde la superficie de la Tierra es 11,2 km/s, lo que equivale a 40 320 km/h. La velocidad de escape de la Luna es de 2,38 km/s, la de Marte 5,027 km/s y la del Sol 617,7 km/s.^{[cita requerida]}

A velocidades inferiores a la de escape, el proyectil se convertiría en un satélite artificial en órbita elíptica alrededor del astro que lo atraiga. Según las dimensiones del astro y la velocidad inicial del proyectil, puede ocurrir que esa trayectoria elíptica se complete o que termine en colisión con el astro que atrae al proyectil. En este segundo caso, suele aproximarse la trayectoria elíptica por una parábola (Tiro parabólico).

Para velocidades superiores a la de escape, el proyectil se elejaría indefinidamete de la Tierra o astro desde el que se lanzó, describiendo una trayectoria abierta del tipo parabólico o hipérbolico, según sea su velocidad de lanzamiento, con uno de sus focos en el centro del astro.

Deducción de la velocidad de escape

Para calcular la velocidad de escape, se usan las siguientes fórmulas relacionadas con la energía cinética y potencial:

${\displaystyle E_{\text{c}}={\frac {1}{2}}mv^{2}\qquad E_{\text{p}}=-G{\frac {Mm}{R}}}$

El principio de conservación de la energía, al que imponemos la condición de que el objeto se aleje hasta una distancia infinita (${\displaystyle R=\infty }$) y quede en reposo, nos permite escribir:

${\displaystyle {\frac {1}{2}}m{v_{e}}^{2}-G{\frac {Mm}{R}}\;=\;0}$

de modo que

${\displaystyle v_{e}={\sqrt {\frac {2GM}{R}}}={\sqrt {2gR}}}$

donde:

• v_e es la velocidad de escape.
• G es la Constante de gravitación universal (6.672×10⁻¹¹ N m²/kg²).
• M es la masa del astro.
• m es la masa del proyectil.
• R es el radio del astro (en el supuesto de forma esférica).
• g es la intensidad del campo gravitatorio en la superficie del astro. En la Tierra, g = 9.81 m/s².