Física - Mecánica clásica

Astrodinámica

periodo orbital es el tiempo que le toma a un astro recorrer su órbita. Cuando se trata de objetos que orbitan alrededor del sol existen dos tipos:

• El periodo sideral es el tiempo que tarda el objeto en dar una vuelta completa alrededor del sol, tomando como punto de referencia una estrella fija. Se considera el auténtico período orbital del objeto y sería el que vería un observador inmóvil que no orbitara alrededor del sol.
• El periodo sinódico es el tiempo que tarda el objeto en volver a aparecer en el mismo punto del cielo respecto al sol, cuando se observa desde la Tierra. Este periodo tiene en cuenta que la Tierra, lugar desde el cual es observado el objeto, también orbita en torno al sol. Es, por tanto, el tiempo que transcurre entre dos conjunciones sucesivas con el sol, y es el período orbital aparente.

El período sideral y el sinódico difieren ya que la Tierra, a su vez, da vueltas alrededor del Sol.

Calcular el periodo sideral

Suponiendo órbitas completamente circulares, la Tierra se movería 360° en un tiempo T de 365.2425 días, mientras que el astro se movería 360° en un tiempo P (periodo sideral o real). Eso es igual al tiempo S (periodo sinódico o aparente) más una compensación por ir más o menos rápido que la Tierra. Se obtiene por lo tanto la siguiente ecuación:

${\displaystyle \left({360grados \over P}\right)\cdot S=\left({360grados \over T}\right)\cdot S\pm 360grados}$

El signo de ±360° es una suma si el astro da una vuelta a su órbita en menor tiempo que la Tierra —sea un planeta interior (diferente a Marte o la propia Tierra) o la Luna—, es una resta si el astro da una vuelta a su órbita en mayor tiempo que la Tierra —sea Marte, un planeta exterior o un planeta enano—.

Simplificando y despejando, usando el álgebra, obtenemos la siguiente fórmula:

${\displaystyle {1 \over P}={1 \over T}\pm {1 \over S}}$

Comprobación

Para comprobar la validez de la fórmula usaremos un caso real: la Luna. Si estamos en la Tierra y observamos la luna a través de los días veremos que tarda aproximadamente 29 d 12 h 44 min en su periodo sinódico (aparente desde la Tierra con respecto al sol) o bien 29.530556 días, lo cual es el valor de S. Sabemos que la Tierra tarda aproximadamente 365.256363 días en dar una vuelta al sol,¹ lo cual será nuestro valor T. La operación queda así:

${\displaystyle {1 \over P}={1 \over 365.256363}+{1 \over 29.530556}=0.036601}$

El signo es positivo dado que da una vuelta a su propia órbita más rápido que la Tierra a la suya. El resultado es redondeado con seis decimales. Es el valor de 1/P y para obtener P (periodo sideral o real, de la luna en este caso) sólo hacemos la operación 1÷0.036601 = 27.321659 días.

Sabemos que el periodo sideral de la luna es de aproximadamente 27 d 7 h 43 min o 27.321529 días, por lo que nuestro resultado se aproxima mucho al valor real.

página de problemas de éste tema .- ..................................................:http://www.elaprendiz.es/F2B_prob_4.htm

El plano orbital de un objeto orbitando alrededor de otro es el plano geométrico en el cual está contenida la órbita. Bastan tres puntos en el espacio para definir el plano orbital: el centro del objeto más pesado, el centro del segundo objeto (objeto que orbita) y el centro de este último objeto transcurrido un tiempo.

Por definición, la inclinación de un planeta en el Sistema Solar es el ángulo entre su plano orbital y el plano orbital de la Tierra. En otros casos, por ejemplo un satélite en órbita en torno a otro planeta, es conveniente definir la inclinación de la órbita del satélite como el ángulo entre su plano orbital y el ecuador del planeta.

De los elementos orbitales, el plano orbital se representa como P1.

 potencial gravitatorio o potencial gravitacional en un punto del campo gravitatorio es una magnitud escalar que se define como el trabajo por unidad de masa que debe realizar una fuerza para transportar un cuerpo, a velocidad constante, desde el infinito hasta un punto del campo gravitatorio. Su unidad en el SI es el julio por kilogramo (J/kg).

Representación gráfica en tres dimensiones de una porción de un potencial gravitatorio alrededor de un cuerpo uniforme esférico. Los puntos de inflexión de la sección transversal se encuentran en la superficie del cuerpo.

Cálculo del potencial gravitatorio

Para una masa puntual

${\displaystyle V=-{\frac {GM}{r}}}$

Donde ${\displaystyle G}$ es la constante de gravitación universal y ${\displaystyle r}$ la distancia del punto de interés a la masa puntual ${\displaystyle M}$.

Para una distribución continua de masa

${\displaystyle V=-G\int _{m}{\frac {1}{r}}\,dm}$

Donde ${\displaystyle r}$ es la distancia desde el punto de interés a cada una de las porciones infinitesimales del cuerpo extenso que genera el campo.

Cálculo a partir del campo gravitatorio

${\displaystyle V_{a}-V_{b}=\int _{\text{a}}^{\text{b}}\mathbf {g} \cdot \mathrm {d} \mathbf {r} \,}$

De esta ecuación se puede deducir la relación inversa:

${\displaystyle \mathbf {g} =-\nabla V}$

El potencial gravitatorio es, junto con la intensidad de campo gravitatorio, la magnitud que se utiliza para cuantificar el campo gravitatorio en un punto. A diferencia del primero, el potencial es una magnitud escalar. Mientras que la intensidad de campo es una magnitud útil para estudiar las fuerzas que aparecen en un cuerpo fruto de la acción gravitatoria, el potencial, como vamos a ver, es útil para estudiar la energía potencial que posee una partícula debido a esta. En este apartado veremos:

• El concepto de potencial gravitatorio y de diferencia de potencial gravitatorio
• La expresión del potencial gravitatorio creado por una masa puntual (o un cuerpo esférico) y sus propiedades
• El potencial gravitatorio creado por varias masas puntuales (o cuerpos esféricos)
• La relación que hay entre potencial e intensidad de campo gravitatorio

¿Empezamos?

Concepto de potencial gravitatorio

Imaginemos una masa m generadora de campo. Si situamos en sus proximidades una masa testigo m', esta contara con una determinada energía potencial gravitatoria. Al igual que ocurría con la fuerza gravitatoria, dicha energía es una magnitud que depende de la masa testigo, por lo que no es exclusiva del campo en sí. Sin embargo, a partir de ella podemos llegar al concepto de potencial y usarlo para cuantificar dicho campo, al igual que hacíamos con el concepto de intensidad de campo gravitatorio a partir de la citada fuerza gravitatoria.

El potencial gravitatorio en un punto es la energía potencial que la unidad de masa m' adquiere al ser colocada sobre dicho punto.

V=Epm'

Donde:

• V es el potencial gravitatorio en un punto del campo gravitatorio. Su unidad de medida en el Sistema Internacional (S.I.) es el julio por kilogramo (J/kg)
• Ep es la energía potencial gravitatoria que adquiere una partícula testigo m' al situarla en ese punto.

El hecho de que todas las magnitudes sean escalares, permite que el estudio del campo gravitatorio sea más sencillo. De esta forma, si conocemos el valor del potencial gravitatorio V en un punto, podemos determinar que la energía potencial gravitatoria de una masa m situada en él es:

Ep=V⋅m

Diferencia de Potencial Gravitatorio

Si dos puntos de un campo gravitatorio poseen distinto potencial, entre ambos puntos existe lo que se denomina una diferencia de potencial, ΔV. Este valor se encuentra íntimamente relacionado con el trabajo gravitatorio. Por definición, el trabajo que realiza la fuerza gravitatoria para trasladar una masa m en el interior de un campo gravitatorio desde un punto A a otro B se obtiene, de acuerdo a lo ya visto en el apartado sobre energía potencial gravitatoria, por medio de la siguiente expresión:

WgA→B=−ΔEp=EpA−EpB

Si aplicamos la definición de potencial gravitatorio, obtenemos que:

WgA→B=EpA−EpB=m⋅VA−m⋅VB=m⋅(VA−VB)

La diferencia de potencial gravitatorio entre dos puntos A y B de un campo gravitatorio es el opuesto del trabajo realizado por el campo para trasladar una unidad de masa desde el punto A al B.

ΔV=VB−VA=−WgA→Bm

Donde la unidad de medida en el Sistema Internacional de la diferencia de potencial gravitatorio es el julio por kilogramo (J/kg).

Potencial gravitatorio creado por una masa puntual

Una única partícula m es capaz de crear un campo gravitatorio a su alrededor. Si en dicho campo introducimos una masa testigo m' , entonces, aplicando la definición de potencial gravitatorio y atendiendo a la definición de energía potencial gravitatoria de dos masas puntuales, nos quedaría que:

V=Epm'=−G⋅M⋅m'rm'=−G⋅mr

El potencial gravitatorio del campo gravitatorio creado por una masa puntual m se obtiene por medio de la siguiente expresión:

V=−G⋅mr

Donde:

• V es el potencial gravitatorio en un punto. Su unidad de medida en el Sistema Internacional ( S.I. ) es el julio por kilogramo ( J/kg )
• G es la constante de gravitación universal. Su valor es G = 6.67·10-11 N·m2/kg2
• m es la masa puntual que crea el campo gravitatorio. Su unidad de medida en el Sistema Internacional ( S.I ) es el kilogramo ( kg )
• r es la distancia entre la masa y el punto donde medimos el potencial. En el Sistema Internacional ( S.I. ) se mide en metros (m).

La expresión anterior también es válida para el potencial que genera una masa esférica, siempre que r > R, siendo R el radio de la esfera.

Propiedades

El potencial de campo gravitatorio creado por una masa puntual o una masa esférica de radio R tiene las siguientes propiedades:

• Depende de la masa que lo crea y es independiente de la masa o masas a las que pueda afectar
• Su valor, como ocurre con la energía potencial, es negativo a una distancia genérica de la masa y aumenta de forma inversamente proporcional a esta hasta llegar a un valor máximo de 0 a una distancia infinita
• Su valor es el mismo para todas las partículas que se sitúan a una determinada distancia de la masa generadora. Dicho con otras palabras: tiene simetría esférica

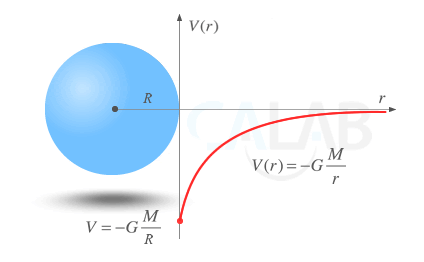
Potencial Gravitatorio

A medida que nos alejamos de la masa generadora de campo el potencial gravitatorio, cuyo valor depende de la masa generadora, aumenta. En el infinito el potencial, al igual que la energía potencial gravitatoria, es cero.