Matemáticas - Fracciones

 problema de Znám pregunta que conjuntos de k enteros tienen la propiedad de que cada entero en el conjunto es un divisor propio del producto de los demás enteros del conjunto más 1. El problema de Znám toma su nombre del matemático eslovaco Štefan Znám, quien lo sugirió en 1972, aunque otros matemáticos ya estaban trabajando con problemas similares en esa misma época. Un problema directamente relacionado ignora la suposición de que el divisor sea propio; recibe por lo tanto el nombre de problema de Znám impropio.

Se puede dar fácilmente una solución para el problema de Znám impropio, dado cualquier k: los primeros k términos de la sucesión de Sylvester cumplen la propiedad pedida. Sun (1983) demostró que hay al menos una solución para el problema de Znám (propio) para cualquier k ≥ 5. La solución de Sun está basada en una recurrencia similar a la de la sucesión de Sylvester, pero con un conjunto distinto de valores iniciales.

El problema de Znám está íntimamente relacionado con las fracciones egipcias. Se sabe que hay solo un número finito de soluciones posibles para cada k. Entre las varias preguntas abiertas en torno al problema, se desconoce si hay alguna solución para el problema usando solo números impares.

Demostración gráfica de que 1 = 1/2 + 1/3 + 1/11 + 1/23 + 1/31 + 1/(2×3×11×23×31). Cada fila de k cuadrados de lado 1/k tiene un área total de 1/k, y todos los cuadrados juntos cubren exactamente un cuadrado de área 1. La fila inferior, con 47058 cuadrados de lado 1/47058 es demasiado pequeño para apreciarse en la figura, por lo que no se muestra.

El problema

El problema de Znám pregunta que conjuntos de k enteros tienen la propiedad de que cada entero en el conjunto es un divisor propio del producto de los demás enteros del conjunto más 1. Esto es, dado k, que conjuntos de enteros

${\displaystyle \{n_{1},\ldots ,n_{k}\}}$

existen, tales que, para cada i, n_i divide, sin ser igual, a

${\displaystyle {\Bigl (}\prod _{j\neq i}^{n}n_{j}{\Bigr )}+1\quad }$

Un problema directamente relacionado trata sobre conjuntos de enteros en los que cada entero en el conjunto es un divisor, no necesariamente propio, de uno más el producto de los demás enteros en el conjunto. Este problema no parece haber recibido ningún nombre en la literatura matemática, por lo que será referido como problema de Znám impropio. Toda solución al problema de Znám es también una solución al problema de Znám impropio, pero el inverso no es necesariamente cierto.

Historia

El problema de Znám recibe su nombre del matemático eslovaco Štefan Znám, que lo enunció en 1972. Barbeau (1971) había planteado su versión impropia para k = 3, y Mordell (1973), con independencia de Znám, encontró todas las soluciones del problema impropio para k ≤ 5. Skula (1975) demostró que el problema es irresoluble para k < 5, y reconoció el mérito de J. Janák por encontrar la solución {2, 3, 11, 23, 31} para k = 5.

Ejemplos

Una solución para k = 5 es {2, 3, 7, 47, 395}. Unos pocos cálculos demuestran que

3 × 7 × 47 × 395	+ 1 =	389866,		que es divisible por 2, pero diferente,
2 × 7 × 47 × 395	+ 1 =	259911,		que es divisible por 3, pero diferente,
2 × 3 × 47 × 395	+ 1 =	111391,		que es divisible por 7, pero diferente,
2 × 3 × 7 × 395	+ 1 =	16591,		que es divisible por 47, pero diferente,
2 × 3 × 7 × 47	+ 1 =	1975,		que es divisible por 395, pero diferente,

Un caso interesante de solución que "casi funciona" para k = 4 es el conjunto {2, 3, 7, 43}, formado por los primeros cuatro términos de los secuencia de Sylvester. Tiene la propiedad de que cada entero del conjunto divide el producto de los demás más uno, pero el último elemento del conjunto es igual al producto de los tres primeros más uno, por lo que no es un divisor propio. Es, por lo tanto, solución al problema impropio de Znám, pero no al propio.

Conexión con las fracciones egipcias

Toda solución del problema de Znám impropio es equivalente (dividiendo por el producto de las x_i) a la solución de la ecuación

${\displaystyle \sum {\frac {1}{x_{i}}}+\prod {\frac {1}{x_{i}}}=y,}$

donde tanto y como cada x_i tienen que ser enteros. A la inversa, toda solución a la ecuación corresponde a una solución del problema de Znám impropio. Sin emabrgo, todas las soluciones conocidas tienen y = 1, por lo que satisfacen la ecuación

${\displaystyle \sum {\frac {1}{x_{i}}}+\prod {\frac {1}{x_{i}}}=1.}$

Es decir, llevan a una representación en forma de fracción egipcia del número uno como suma de fracciones unitarias. Varios de los artículos citados en referencia al problema de Znám estudian también las soluciones a dicha ecuación. Brenton y Hill (1988) describe una aplicación de la ecuación en topología, a la clasificación de singularidades en superficies, y Domaratzki et al. (2005) describe una aplicación a la teoría de autómatas finitos no deterministas.

Número de soluciones

Como Janák y Skula (1978) demostró, el número de soluciones para cualquier k es finito, por lo que tiene sentido contar el número total de soluciones para cada k.

Brenton y Vasiliu calcularon que el número de soluciones para valores pequeños de k, empezando con k = 5, forma la secuencia

2, 5, 18, 96 (sucesión A075441 en OEIS).

Actualmente se conocen unas pocas soluciones para k = 9 y k = 10, pero no se sabe cuantas soluciones faltan por descubrir para esos valores de k. Sin embargo, hay infinitas soluciones si no se fija k: Cao y Jing (1998) demostró que hay al menos 39 soluciones para cada k ≥ 12, mejorando los resultados anterior sobre existencia de soluciones hechos por (Cao, Liu y Zhang, 1987 y Sun y Cao, 1988). Sun y Cao (1988) conjeturó que el número de soluciones para cada valor de k crece monótonamente con k.

Se desconoce si existen soluciones al problema de Znám usando solo números impares. Con una excepción, todas las soluciones conocidas empiezan por 2. Si todos los números en una solución a cualquiera de las dos versiones del problema son primos, su producto es un número pseudoperfecto primario (Butske, Jaje y Mayernik, 2000); también se ignora si existen infinitas soluciones de este tipo.

 proporcionalidad es una relación o razón constante entre magnitudes medibles."Si uno aumenta o disminuye el otro también aumenta o disminuye proporcionalmente".

Símbolo

El símbolo matemático '∝' se utiliza para indicar que dos valores son proporcionales. Por ejemplo: A ∝ B. En Unicode el símbolo es U+221D.

Proporcionalidad directa

Dadas dos variables X y Y, Y es (directamente) proporcional a X (X y Y varían directamente, o X y Y están en variación directa) si hay una constante 'que distinta de cero tal que:

${\displaystyle y=kx.\,}$

La relación a menudo se denota

Los dos rectángulos con franjas son semejantes, los cocientes de sus dimensiones se indican horizontalmente en la imagen. La duplicación de la escala del triángulo con franjas se indica oblicuamente en la imagen.

${\displaystyle y\propto x}$

y la razón constante

${\displaystyle k=y/x\,}$

es llamada constante de proporcionalidad.

Para ilustrar, supongamos que si dividimos el peso de una muestra de hierro por su volumen, el resultado será el mismo que el obtenido al dividir el peso de cualquier otra muestra por su volumen, dicho cociente corresponde a la constante de proporcionalidad.¹

Primer ejemplo

La receta de un pastel de vainilla indica que para cuatro personas se necesitan 200 g de harina, 150 g de mantequilla, cuatro huevos y 120 g de azúcar. ¿Cómo adaptar la receta para cinco personas? Según varios estudios, la mayoría de la gente calcularía las cantidades para una persona (dividiendo entre cuatro) y luego las multiplicaría por el número real de personas, cinco, otras solo le sumarían lo que a una persona le corresponde. Una minoría no siente la necesidad de pasar por las cantidades unitarias (es decir por persona) y multiplicaría los números de la receta por 5/4 = 1,25 (lo que equivale a añadir cinco huevos, 250 g de harina; 187,5 g de mantequilla y 150 g de azúcar).

Se dice que la cantidad de cada ingrediente es proporcional al número de personas y se representa esta situación mediante una tabla de proporcionalidad: coeficiente k no nulo (${\displaystyle 5 \over 4}$ en el ejemplo) tal que

${\displaystyle y_{1}=k\cdot x_{1},y_{2}=k\cdot x_{2}\quad ...\quad y_{n}=k\cdot x_{n}\ }$

recta que pasa por el origen de coordenadas

Si se consideran ${\displaystyle x_{1},x_{2}...x_{n}\ }$ e ${\displaystyle y_{1},y_{2}...y_{n}\ }$ como valores de variables ${\displaystyle x\ }$ e ${\displaystyle y\ }$, entonces se dice que estas variables son proporcionales; la igualdad y = k·x significa que y es una Función lineal de x.
La representación gráfica de esta función es una recta que pasa por el origen del sistema de coordenadas. Una variación (incremento o decremento) de x da lugar a una variación proporcional de y (y recíprocamente, puesto que k≠0: y = 1/k · x):

${\displaystyle \Delta y=k\cdot \Delta x\ }$

Son las funciones más sencillas que existen y las primeras que se estudian en clase de matemáticas, con alumnos de trece años aproximadamente.

La relación «Ser proporcional a» es

• reflexiva ( toda variable es proporcional a sí misma, con el coeficiente 1)
• simétrica (cuando y es proporcional a x entonces x lo es a y, con el coeficiente inverso) y
• transitiva (si x es proporcional a y, e y a z, entonces x lo es con z, multiplicando los coeficientes)

por lo que se trata de una relación de equivalencia. En particular dos variables proporcionales a una tercera serán proporcionales entre sí).

La tabla del primer ejemplo se puede descomponer en tres de formato dos por dos:

por tanto las propiedades de la proporcionalidad se ilustran preferentemente con tablas de cuatro casillas.

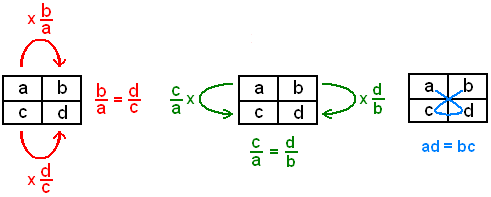
Una proporción está formada por los números a, b, c y d, si la razón entre a y b es la misma que entre c y d.

Una proporción está formada por dos razones iguales: a : b = c : d

Dónde a, b, c y d son distintos de cero y se lee a es a b como c es a d .

Proporción múltiple:

Una serie de razones está formada por tres o más razones iguales: a : b = c : d = e : f

Y se puede expresar como una proporción múltiple: a : c : e = b : d : f

En la proporción hay cuatro términos; a y d se llaman extremos; c y b se llaman medios.

En toda proporción el producto de los extremos es igual al producto de los medios.

Para establecer que una tabla es proporcional, se puede:

1. verificar que la segunda columna es múltiple de la primera, (primera tabla: para pasar de la primera casilla a la segunda, hay que multiplicar por ${\displaystyle b \over a}$; en la segunda línea se tiene que multiplicar por ${\displaystyle d \over c}$, luego estas fracciones deben ser iguales para obtener columnas proporcionales)
2. verificar que la segunda línea es múltiple de la primera (segunda tabla, con un raciocinio parecido) o
3. verificar la igualdad de los productos cruzados: a·d = b·c. (tercera tabla: las igualdades anteriores equivalen a a·d = b·c, cuando no hay valores nulos, que por cierto no tienen un gran interés en este contexto). ya que no se puede comprobar el número

Segundo ejemplo

Dos albañiles construyeron un muro de doce metros cuadrados de superficie en tres horas; ¿ Qué superficie construirán cinco albañiles en cuatro horas ?

Hay dos parámetros que influyen en la superficie construida: El número de albañiles y el tiempo de trabajo. No hay que resistir a la tentación de aplicar dos veces la proporcionalidad, pero eso sí, explicitando las hipótesis subyacentes.

Afirmar que el trabajo realizado es proporcional al número de albañiles equivale a decir que todos los obreros tienen la misma eficacia al trabajo (son intercambiables); y afirmar que la superficie es proporcional al tiempo de trabajo supone que el rendimiento no cambia con el tiempo: los albañiles no se cansan.

Admitiendo estas dos hipótesis, se puede contestar a la pregunta pasando por una etapa intermedia: ¿ Qué superficie construirían dos albañiles en cuatro horas ? El parámetro "número de albañiles" tiene un valor fijo, luego se aplica la proporcionalidad con el tiempo (subtabla roja). La superficie construida será multiplicada por ${\displaystyle 4 \over 3}$. Luego, fijando el parámetro tiempo a cuatro horas, y variando él del número de obreros de 2 a 5, la superficie será multiplicada por ${\displaystyle 5 \over 2}$ (la subtabla azul es proporcional).

El resultado final es

${\displaystyle 12\times {\frac {4}{3}}\times {\frac {5}{2}}=40}$

metro cuadrado.

La proporcionalidad múltiple se resuelve así, multiplicando por los coeficientes correspondientes a cada factor:

Tercer ejemplo

Dos autos recorren exactamente el mismo camino. Al primero le ha tomado dos horas y media llegar al destino, rodando a una velocidad promedia de 70 km/h. El segundo rueda a 100 km/h. ¿Cuánto tiempo ha tardado en llegar?

Cuanta mayor velocidad tenga uno, menor tiempo durará el viaje. Si se multiplica por dos la velocidad, la duración del viaje se dividirá en dos. Aquí, claramente el tiempo del recorrido no es proporcional a la velocidad sino justamente lo contrario: es inversamente proporcional, es decir proporcional a la inversa de la velocidad. Esto permite responder a la pregunta:

cambiando una multiplicación por una división (primera tabla) o aplicando la proporcionalidad con la inversa de la velocidad (segunda tabla). El tiempo será ${\displaystyle 2,5\times {\frac {7}{10}}=1,75}$, es decir una hora y 45 minutos.

Más generalmente, si una variable y es inversamente proporcional a otra variable x, se puede aplicar la proporcionalidad con ${\displaystyle 1 \over x}$, o más bien utilizar la siguiente equivalencia:

Es decir que el producto de los valores correspondientes (aquí en la misma línea) es constante. En el ejemplo: 70 × 2,5 = 100 × 1, 75 = 175 km, que es la longitud del recorrido.

Una tabla de variación proporcional es aquella que sigue una secuencia utilizando de base el precio de algún objeto u otra cosa que pueda aumentar o disminuir cierto número u objeto de forma proporcional. ejem:

número de canicas precio

2 canicas 50 centavos

4 canicas 1 peso

6 canicas 1,50 pesos

Magnitudes Directamente Proporcionales:

Dos magnitudes son directamente proporcionales cuando al multiplicar o dividir una de ellas por un número, la otra queda multiplicada o dividida respectivamente por el mismo número.

Ejemplo:

Un automóvil consume 3 galones de gasolina por 120 km de recorrido ¿Cuantos kilómetros recorre con 20 galones?

Observamos que las magnitudes son directas Si la razón o cociente entre ellas es un valor constante. Con los datos de la tabla, hallamos la razón.

Elaboramos una tabla de proporcionalidad:

Gasolina 3 1 10 20 40 (galones)

Recorrido 120 40 400 800 1600 (kilómetros)

Con 20 galones de gasolina, el auto recorre 800 kilómetros: Mientras más kilómetros se recorran, más galones de gasolina se consumirán. El número de kilómetros recorridos es directamente proporcional (D.P) al número de galones de gasolina. Siempre que las demás condiciones se mantuvieran constantes. Significa, que no se modificaran las condiciones climáticas o geográficas que modificaran el consumo.

Aplicación en geometría

El concepto de proporcionalidad es equivalente al de semejanza cuando se comparan dos triángulos semejantes. De hecho las propiedades de la proporcionalidad (reflexividad, simetría y transitividad) son las mismas que las de la semejanza.

Propiedades

Ya que

${\displaystyle y=kx\,}$

es equivalente a

${\displaystyle x=\left({\frac {1}{k}}\right)y,}$

se sigue que si y es proporcional a x, con constante de proporcionalidad k distinta de cero, entonces x es también proporcional a y con constante de proporcionalidad 1/k.

Si y es proporcional a x, entonces el gráfico de y como función de x será una línea recta que pasa por el origen con la pendiente de la línea igual a la constante de proporcionalidad: corresponde a un crecimiento lineal.

Proporcionalidad inversa

El concepto de proporcionalidad inversa puede ser contrastado contra la proporcionalidad directa. Considere dos variables que se dice son "inversamente proporcionales" entre sí. Si todas las otras variables se mantienen constantes, la magnitud o el valor absoluto de una variable de proporcionalidad inversa disminuirá proporcionalmente si la otra variable aumenta, mientras que su producto se mantendrá (la constante de proporcionalidad k) siempre igual.

Formalmente, dos variables son inversamente proporcionales (o están en variación inversa, o en proporción inversa o en proporción recíproca) si una de las variables es directamente proporcional con la multiplicativa inversa (recíproca) de la otra, o equivalentemente, si sus productos son constantes. Se sigue que la variable y es inversamente proporcional a la variable x si existe una constante k distinta de cero tal que

${\displaystyle y={k \over x}}$

Factor constante de proporcionalidad

La constante, o factor de proporcionalidad, puede ser encontrada multiplicando la variable "x" original y la variable "y" original.

Mejor definido en palabras sencillas es que cuando una cantidad o variable sube proporcionalmente la otra variable baja o viceversa.

Como ejemplo, el tiempo consumido en una travesía es inversamente proporcional a la velocidad del viaje; el tiempo necesitado para cavar un hoyo es (aproximadamente) inversamente proporcional al número de personas cavando.

El gráfico de dos variables variando inversamente en un plano de coordenadas cartesianas es una hipérbola. El producto de los valores X e Y de cada punto de esa curva igualarán la constante de proporcionalidad (k). Ya que ni x ni y pueden ser igual a cero (si k es distinta de), la curva nunca cruzará ningún eje.

Coordenadas hiperbólicas

Los conceptos de proporción directa e inversa conllevan a la ubicación y puntos en el plano cartesiano por coordenadas hiperbólicas; las dos coordenadas corresponden a la constante de proporcionalidad directa que ubica un punto en un rayo y la constante de proporcionalidad inversa que posiciona un punto en una hipérbola.

Proporcionalidad exponencial y logarítmica

Una variable y es proporcionalmente exponencial a una variable x, si y es directamente proporcional a la función exponencial de x, esto es si existen constantes k y a diferentes de cero.

${\displaystyle y=ka^{x}.\,}$

Del mismo modo, una variable y es logaritmicamente proporcional a una variable x, si y es directamente proporcional al logaritmo de x, esto es si existen las constantes k y a distintas de cero.

${\displaystyle y=k\log _{a}(x).\,}$

Determinación experimental

Para determinar experimentalmente si dos cantidades físicas son directamente proporcionales, uno realiza diversas mediciones y plotea los puntos resultantes de la data en un sistema de coordenadas cartesianas. Si los puntos caen en o cerca de una línea recta que pasa por el origen (0, 0), entonces las dos variables son probablemente proporcionales, con la constante de proporcionalidad dada por la pendiente de la línea.

Relación de equivalencia

La proporcionalidad es una relación de equivalencia en un conjunto ${\displaystyle \mathbb {R} \setminus \{0\}}$ (o incluso ${\displaystyle \mathbb {C} \setminus \{0\}}$). Esto es porque es: reflexiva, simétrica ytransitiva. Esto se prueba a continuación usando la definición: si a∝b entonces

${\displaystyle a=kb}$, _{donde k es una constante diferente de cero.}

Reflexividad

Para todo ${\displaystyle a\in \mathbb {R} \setminus \{0\}}$,

${\displaystyle a=1\cdot a}$

Por lo tanto, como uno es una constante diferente de cero,

${\displaystyle a\propto a}$

Simetría

Supongase que ${\displaystyle a,b\in \mathbb {R} \setminus \{0\}}$ y a∝b, entonces,

${\displaystyle a=kb\,}$

en donde k es una constante diferente de cero. Dividiendo por k, tenemos:

${\displaystyle b={\frac {a}{k}}={\frac {1}{k}}\cdot a}$

Como k es diferente de cero, 1/k es también diferente de cero. De modo que:

${\displaystyle b\propto a}$

Transitividad

Supongase que ${\displaystyle a,b,c\in \mathbb {R} \setminus \{0\}}$, a∝b y b∝c. Entonces,

${\displaystyle a=kb\,}$

y,

${\displaystyle b=nc\,}$

en donde k y n son constantes distintas de cero. Substituyendo la segunda ecuación en la primera, tenemos:

${\displaystyle a=k\cdot (nc)=(kn)\cdot c}$

Como k y n son diferentes a cero, kn debe ser también diferente de cero. Por lo tanto:

${\displaystyle a\propto c}$

Repartos proporcionales

Antecedente histórico

Las primeras compañías europeas fueron fundadas por armadores navieros de Italia. Empiezan en el siglo IX. La aritmética negocial, tomada de los árabes por Leonardo de Pisa, tuvo una gran aceptación y uso en Europa en esa época. Se aplicaba en la resolución de problemas vinculados en la repartición de beneficios y pérdidas que acarreaban las actividades de dichas empresa navales.

Casos de repartos proporcionales

Estos consisten en distribuir un número en partes proporcionales a otros varios y diversos. Pueden presentarse los repartos directos o inversos o compuestos.

"Para repartir un número dato en partes directamente proporcionales a diversos números enteros positivos, se multiplica el número a repartir por cada uno de los enteros y se divide por la suma de todos ellos". Ejemplo

Repartir 120 en partes directamente proporcionales a 2, 3 y 5.

Solución de la ecuación: El primero recibirá 2k, el segundo 3k y el tercero 5k. Los tres reciben 2k + 3k + 5k = 120, de donde 10k = 120. De modo que la incógnita k = 120/10 = 12.

Así al primero le toca 12 x 2 = 24; al segundo, 12 x 3 = 36; al tercero, 12 x 5 = 60.

En partes inversamente proporcionales

Un padre dispone que , en caso de falecimiento, sus 6.200 acciones bancarias se repartan en partes inversamente proporcionales a las edades de su hijos que tienen 4, 6 y 10 años respectivamnente.

Esto significa que debe recibir más el que tiene menos edad y menos el de más edad.

En este caso se divide en partes 'directamente proporcionales a 1/4, a 1/6 y 1/10. Que llevados a mínimo común denominador, resultan: 15/60, 10/60 y 6/60.

Luego se reparte en partes directamente proporcionales a 15, 10 y 6. Resultando:

El menor con 3.000 acciones; el intermedio, 2.000; y el mayor, con 1.200 acciones.