Física - Mecánica clásica

Astrodinámica

La longitud del nodo ascendente (${\displaystyle \Omega \,}$) es uno de los elementos orbitales utilizados para especificar la órbita de un cuerpo celeste. Para un objeto que orbita el Sol, es el ángulo, con vértice en el Sol, que va desde el punto Aries hasta el nodo ascendente de la órbita del objeto, medido en el plano de referencia de la eclíptica y en sentido directo.

Elementos orbitales de un cuerpo alrededor del Sol.

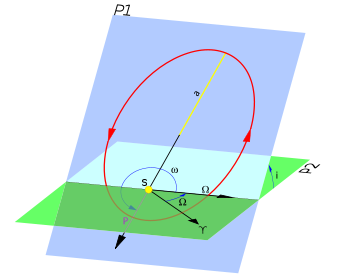
La ${\displaystyle {\bar {\omega }}\,}$ (longitud del periastro), es la suma de dos ángulos medidos en planos distintos: la Longitud del nodo ascendente (${\displaystyle \Omega \,\!}$) medido sobre el plano de referencia, y el Argumento del periastro (${\displaystyle \omega \,\!}$) medido sobre al plano de la órbita:

${\displaystyle {\bar {\omega }}=\Omega +\omega \,}$

En el caso del Sol se llama longitud del perihelio y en el caso de la Tierra longitud del perigeo.

Elementos orbitales de un cuerpo alrededor del Sol.

la longitud media es la longitud a la que un cuerpo orbitando podría encontrarse si su órbita fuese circular y su inclinación fuese nula. La longitud media cambia uniformemente con el tiempo. Los únicos instantes en es igual a la longitud verdadera son el periastro y el apoastro.

La longitud media ${\displaystyle L\,}$ puede calcularse como sigue:

${\displaystyle L=M+{\bar {\omega }}=M+\Omega +\omega \,}$

donde:

• ${\displaystyle M\,}$ es la anomalía media,
• ${\displaystyle {\bar {\omega }}\,}$ es la longitud del periastro,
• ${\displaystyle \Omega \,}$ es la longitud de nodo ascendente y
• ${\displaystyle \omega \,}$ es el argumento del periastro.

${\displaystyle L=M+{\bar {\omega }}=M+\Omega +\omega \,}$

Elementos orbitales de un cuerpo alrededor del Sol.

La masa reducida es un concepto que permite resolver el problema de los dos cuerpos de la mecánica como si fuese un problema de un cuerpo. Dados dos cuerpos, uno con masa ${\displaystyle m_{1}}$ y el otro con masa ${\displaystyle m_{2}}$, orbitarán el baricentro. El equivalente al problema de un cuerpo, teniendo la posición de un cuerpo respecto al otro como incógnita es la de un cuerpo único con masa inercial

${\displaystyle m_{red}\equiv \mu \equiv {1 \over {{1 \over m_{1}}+{1 \over m_{2}}}}={{m_{1}m_{2}} \over {m_{1}+m_{2}}}}$

con la fuerza el uno.

Aplicando la fórmula de la gravedad se obtiene la posición de los cuerpos como si sólo existiese un único cuerpo en el baricentro de masa ${\displaystyle {{m_{1}m_{2}} \over {m_{red}}}=m_{1}+m_{2}}$ y la masa de los dos cuerpos no afectase.

EL PROBLEMA DE DOS CUERPOS. MASA REDUCIDA  Introducimos ahora una cantidad llamada masa reducida del sistema de dos partículas y designada por μ , que definimos por : 1μ=1m1+1m2=m1+m2m1⋅m2 μ=m1⋅m2m1+m2 Podemos escribir entonces la ecuación (A) en la forma: a12=F12μ⇒F12=μ⋅a12 De donde podemos enunciar que el movimiento relativo de dos partículas sujetas únicamente a una interacción mutua es equivalente al movimiento, relativo a un observador inercial, de una partícula de masa igual a la masa reducida bajo una fuerza igual a la interacción.

Por ejemplo, podemos reducir el movimiento de la luna relativo a la tierra a un problema de una única partícula usando la masa reducida del sistema luna-tierra y una fuerza igual a la atracción de la tierra sobre la luna. De la misma forma, cuando hablamos del movimiento de un electrón alrededor del núcleo, podemos suponer el sistema reducido a una partícula con masa igual a la masa reducida del sistema electrón-núcleo moviéndose bajo la fuerza entre el electrón y el núcleo. Por consiguiente, al describir el movimiento de dos partículas bajo su interacción mutua podemos separar el movimiento del sistema en el movimiento del centro de masa cuya velocidad es constante, y el movimiento de las dos partículas, dado por las ecuaciones desarrolladas anteriormente, referido a un sistema de referencia ligado al centro de masa. Cuando una de las partículas tiene una masa mucha mas pequeña de la otra, por ejemplo la m1, la masa reducida se puede escribir: μ=m11+m1/m2≅m1(1−m1m2) Donde hemos empleado la aproximación (1+x)n≅1+nx( cuando x<<1) Esto conduce a una masa reducida aproximadamente igual a la masa de la partícula mas ligera. Por ejemplo, al discutir el movimiento de un satélite artificial alrededor de la tierra podemos usar, con muy buena aproximación, la masa del satélite y no la masa reducida del sistema tierra-satélite. Por otra parte, cuando las dos partículas tienen la misma masa (m1=m2) se tiene: μ=12⋅m1 Esta ecuación se puede emplear para el caso de dos protones interactuando entre si y también, con muy buena aproximación para un sistema formado por un neutrón y un protón, tal como ocurre en el deuterón.