GEOMETRÍA ANALÍTICA - CURVAS

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Curva cúbica de Bézier con cuatro puntos de control.

La base funciona en el rango t en [0,1] para curvas de Bézier cúbicas: azul: y = (1 - t ) ³ , verde: y = 3 (1 - t ) ² t , rojo: y = 3 (1 - t ) t ² , y cian: y = t ³ .

Una curva de Bézier (pronunciada[bezje] en francés) es una curva paramétrica utilizada en gráficos de computadora y campos relacionados. ^[1] La curva, relacionada con el polinomio de Bernstein , lleva el nombre de Pierre Bézier , quien la usó en la década de 1960 para diseñar curvas para la carrocería de losautomóviles Renault . ^[2]Otros usos incluyen el diseño de fuentes de computadoray animaciones. ^[2] Las curvas de Bézier pueden combinarse para formar una spline de Bézier , o generalizarse a dimensiones más altas para formar superficies de Bézier . ^[2] El triángulo de Bézier. Es un caso especial de este último.

En los gráficos vectoriales , las curvas de Bézier se utilizan para modelar curvas suaves que se pueden escalar indefinidamente. Las "rutas", como se las conoce comúnmente en los programas de manipulación de imágenes, ^{[nota 1]} son combinaciones de curvas de Bézier vinculadas. Las rutas no están limitadas por los límites de las imágenes rasterizadasy son intuitivas de modificar.

Las curvas de Bézier también se utilizan en el dominio del tiempo, particularmente en animación , diseño de la interfaz de usuario ^{[nota 2]} y suavización de la trayectoria del cursor en las interfaces controladas por la mirada. ^[3] Por ejemplo, una curva de Bézier se puede usar para especificar la velocidad a lo largo del tiempo de un objeto, como un icono que se mueve de A a B, en lugar de simplemente moverse a un número fijo de píxeles por paso. Cuando los animadores o diseñadores de interfaces hablan sobre la "física" o "sensación" de una operación, pueden referirse a la curva Bézier particular utilizada para controlar la velocidad en el tiempo del movimiento en cuestión.

Esto también se aplica a la robótica donde el movimiento de un brazo de soldadura, por ejemplo, debe ser suave para evitar un desgaste innecesario.

La base matemática de las curvas de Bézier, el polinomio de Bernstein , se conocía desde 1912, pero los polinomios no se aplicaron a los gráficos hasta unos 50 años más tarde, cuando fueron ampliamente publicitados por el ingeniero francés Pierre Bézier , quien los utilizó para diseñar carrocerías de automóviles. en Renault . Sin embargo, el estudio de estas curvas fue desarrollado por primera vez en 1959 por el matemático Paul de Casteljau utilizando el algoritmo de Casteljau , un método numéricamente estable para evaluar las curvas de Bézier en Citroën , otro fabricante de automóviles francés.

Aplicaciones [ editar ]

Gráficos por computadora [ editar ]

Ruta Bézier en Adobe Illustrator

Las curvas de Bézier son ampliamente utilizadas en gráficos de computadora para modelar curvas suaves. Como la curva está completamente contenida en el casco convexo de sus puntos de control , los puntos pueden visualizarse gráficamente y usarse para manipular la curva de manera intuitiva. Las transformaciones afines , como la traslación y la rotación, se pueden aplicar en la curva aplicando la transformación respectiva en los puntos de control de la curva.

Las curvas de Bézier cuadráticas y cúbicas son las más comunes. Las curvas de mayor grado son más costosas de evaluar computacionalmente . Cuando se necesitan formas más complejas, las curvas de Bézier de orden bajo se parchean juntas, produciendo una curva de Bézier compuesta . Una curva de Bézier compuesta se conoce comúnmente como "ruta" en lenguajes de gráficos vectoriales (como PostScript ), estándares de gráficos vectoriales (como SVG ) y programas de gráficos vectoriales (como Artline , Timeworks Publisher , Adobe Illustrator , CorelDraw e Inkscape ). Para garantizar la suavidad (Continuidad C ^{1 [ aclaración necesaria ]} ), el punto de control en el que se encuentran dos curvas debe estar en la línea entre los dos puntos de control en cada lado.

El método más sencillo para convertir ( rasterizar ) una curva de Bézier mediante el escaneo es evaluarla en muchos puntos muy próximos y convertir la secuencia aproximada de los segmentos de línea. Sin embargo, esto no garantiza que la salida rasterizada se vea lo suficientemente suave, ya que los puntos pueden estar demasiado separados. A la inversa, puede generar demasiados puntos en áreas donde la curva es casi lineal. Un método de adaptación común es la subdivisión recursiva, en la cual los puntos de control de una curva se verifican para ver si la curva se aproxima a una línea recta dentro de una pequeña tolerancia. Si no, la curva se subdivide paramétricamente en dos segmentos, 0 ≤ t ≤ 0.5 y 0.5 ≤ t≤ 1, y el mismo procedimiento se aplica recursivamente a cada mitad. También hay métodos de diferenciación hacia adelante, pero se debe tener mucho cuidado para analizar la propagación de errores. ^{[ cita requerida ]}

Los métodos analíticos en los que un Bézier se intersecta con cada línea de exploración implican encontrar raíces de polinomios cúbicos (para Béziers cúbicos) y tratar con múltiples raíces, por lo que no se utilizan a menudo en la práctica. ^[5]

Animacion [ editar ]

En aplicaciones de animación, como Adobe Flash y Synfig , las curvas de Bézier se utilizan para delinear, por ejemplo, el movimiento. Los usuarios delinean la ruta deseada en las curvas de Bézier, y la aplicación crea los marcos necesarios para que el objeto se mueva a lo largo de la ruta. ^[6] [7]

Para la animación 3D, las curvas de Bézier se utilizan a menudo para definir rutas 3D, así como curvas 2D para la interpolación de fotogramas clave. ^{[ cita requerida ]} . Las curvas de Bézier ahora se utilizan con mucha frecuencia para controlar la aceleración de la animación en CSS , JavaScript y JavaFx .

Fuentes [ editar ]

Las fuentes TrueType utilizan curvas compuestas de Bézier compuestas de curvas cuadráticas de Bézier. Otros lenguajes y herramientas de imagen (como PostScript , Asymptote , Metafont y SVG ) usan Béziers compuestos compuestos de curvas de Bézier cúbicas para dibujar formas curvas. Las fuentes OpenType pueden usar cualquier tipo, dependiendo del tipo de fuente. ^[8]

La representación interna de todas las curvas de Bézier en fuentes o gráficos vectoriales las dividirá recursivamente hasta el punto donde la curva es lo suficientemente plana como para dibujarla como una serie de segmentos lineales o circulares. El algoritmo de división exacto depende de la implementación, solo se deben respetar los criterios de planitud para alcanzar la precisión necesaria y para evitar cambios locales de curvatura no monotónicos. La característica de "curva suave" de los gráficos en Microsoft Excel también utiliza este algoritmo. ^[9]

Debido a que los arcos de círculos y elipsis no se pueden representar exactamente mediante curvas de Bézier, primero se aproximan mediante curvas de Bézier, que a su vez se aproximan mediante arcos de círculos. Esto es ineficiente ya que también existen aproximaciones de todas las curvas de Bézier que usan arcos de círculos o elipsis, que se pueden representar incrementalmente con precisión arbitraria. Otro enfoque, utilizado por los modernos adaptadores de gráficos de hardware con geometría acelerada, puede convertir exactamente todas las curvas (o superficies) de Bézier y cónicas en NURBS , que se pueden representar de manera incremental sin dividir primero la curva de forma recursiva para alcanzar la condición de planitud necesaria. Este enfoque también permite preservar la definición de la curva en todas las transformaciones y proyecciones lineales o en perspectiva 2D y 3D. ^{[ cita requerida]}

Los motores de fuentes, como FreeType , dibujan las curvas (y líneas) de la fuente en una superficie pixelada mediante un proceso conocido como rasterización de fuentes . ^[10]

Casos específicos [ editar ]

Una curva de Bézier se define por un conjunto de puntos de control P ₀ a P _n , donde n se denomina orden ( n = 1 para lineal, 2 para cuadrática, etc.). Los primeros y últimos puntos de control son siempre los puntos finales de la curva; sin embargo, los puntos de control intermedios (si los hay) generalmente no se encuentran en la curva. Las sumas en las siguientes secciones deben entenderse como combinaciones afines , los coeficientes suman 1.

Curvas lineales de Bézier [ editar ]

Dados los distintos puntos P ₀ y P ₁ , una curva lineal de Bézier es simplemente una línea recta entre esos dos puntos. La curva está dada por

$${\ displaystyle \ mathbf {B} (t) = \ mathbf {P} _ {0} + t (\ mathbf {P} _ {1} - \ mathbf {P} _ {0}) = (1-t) \ mathbf {P} _ {0} + t \ mathbf {P} _ {1} {\ mbox {,}} 0 \ leq t \ leq 1}

y es equivalente a la interpolación lineal .

Las curvas de Bézier cuadráticas [ editar ]

Béziers cuadráticos en el arte de las cuerdas: los puntos finales ( • ) y el punto de control ( × ) definen la curva Bézier cuadrática ( ⋯ ).

Una curva de Bézier cuadrática es la trayectoria trazada por la función B ( t ), dados los puntos P ₀ , P ₁ y P ₂ .

$${\ displaystyle \ mathbf {B} (t) = (1-t) [(1-t) \ mathbf {P} _ {0} + t \ mathbf {P} _ {1}] + t [(1- t) \ mathbf {P} _ {1} + t \ mathbf {P} _ {2}] {\ mbox {,}} 0 \ leq t \ leq 1},

que puede interpretarse como el interpolante lineal de los puntos correspondientes en las curvas lineales de Bézier de P ₀ a P ₁ y de P ₁ a P _2,respectivamente. Reorganizando los rendimientos de la ecuación anterior:

$${\ displaystyle \ mathbf {B} (t) = (1-t) ^ {2} \ mathbf {P} _ {0} +2 (1-t) t \ mathbf {P} _ {1} + t ^ {2} \ mathbf {P} _ {2} {\ mbox {,}} 0 \ leq t \ leq 1.}

Esto se puede escribir de una manera que resalte la simetría con respecto a P ₁ :

$${\ displaystyle \ mathbf {B} (t) = \ mathbf {P} _ {1} + (1-t) ^ {2} (\ mathbf {P} _ {0} - \ mathbf {P} _ {1 }) + t ^ {2} (\ mathbf {P} _ {2} - \ mathbf {P} _ {1}) {\ mbox {,}} 0 \ leq t \ leq 1.}

Lo que inmediatamente da la derivada de la curva de Bézier con respecto a t :

$${\ displaystyle \ mathbf {B} '(t) = 2 (1-t) (\ mathbf {P} _ {1} - \ mathbf {P} _ {0}) + 2t (\ mathbf {P} _ { 2} - \ mathbf {P} _ {1}) \ ,.}

de donde se puede concluir que las tangentes a la curva en P ₀ y P _{2 se}intersecan en P ₁ . A medida que t aumenta de 0 a 1, la curva parte de P ₀ en la dirección de P ₁ , luego se dobla para llegar a P ₂ desde la dirección de P ₁ .

La segunda derivada de la curva de Bézier con respecto a t es

$${\ displaystyle \ mathbf {B} '' (t) = 2 (\ mathbf {P} _ {2} -2 \ mathbf {P} _ {1} + \ mathbf {P} _ {0}) \ ,. }

Las curvas de Bézier cúbicos [ editar ]

Cuatro puntos P ₀ , P ₁ , P ₂ y P ₃ en el plano o en un espacio de dimensión superior definen una curva de Bézier cúbica. La curva comienza en P _{0 y} va hacia P ₁ y llega a P ₃ desde la dirección de P ₂ . Por lo general, no pasará por P ₁ o P ₂ ; Estos puntos solo están ahí para proporcionar información direccional. La distancia entre P ₁ y P ₂determina "a qué distancia" y "a qué velocidad" se mueve la curva hacia P ₁ antes de girar hacia P ₂ .

Al escribir B _{P i , P j , P k} ( t ) para la curva de Bézier cuadrática definida por los puntos P _i , P _j y P _k , la curva de Bézier cúbica se puede definir como una combinación afín de dos curvas de Bézier cuadráticas:

$${\ displaystyle \ mathbf {B} (t) = (1-t) \ mathbf {B} _ {\ mathbf {P} _ {0}, \ mathbf {P} _ {1}, \ mathbf {P} _ {2}} (t) + t \ mathbf {B} _ {\ mathbf {P} _ {1}, \ mathbf {P} _ {2}, \ mathbf {P} _ {3}} (t) { \ mbox {,}} 0 \ leq t \ leq 1.}

La forma explícita de la curva es:

$${\ displaystyle \ mathbf {B} (t) = (1-t) ^ {3} \ mathbf {P} _ {0} +3 (1-t) ^ {2} t \ mathbf {P} _ {1 } +3 (1-t) t ^ {2} \ mathbf {P} _ {2} + t ^ {3} \ mathbf {P} _ {3} {\ mbox {,}} 0 \ leq t \ leq 1.}

Para algunas opciones de P ₁ y P _2, la curva puede intersecarse o contener una cúspide .

Cualquier serie de 4 puntos distintos se puede convertir en una curva de Bézier cúbica que recorre los 4 puntos en orden. Dado el punto inicial y final de alguna curva de Bézier cúbica, y los puntos a lo largo de la curva correspondientes a t = 1/3 yt = 2/3, los puntos de control para la curva de Bézier original se pueden recuperar. ^[11]

La derivada de la curva de Bézier cúbica con respecto a t es

$${\ displaystyle \ mathbf {B} '(t) = 3 (1-t) ^ {2} (\ mathbf {P} _ {1} - \ mathbf {P} _ {0}) + 6 (1-t ) t (\ mathbf {P} _ {2} - \ mathbf {P} _ {1}) + 3t ^ {2} (\ mathbf {P} _ {3} - \ mathbf {P} _ {2}) \ ,.}

La segunda derivada de la curva de Bézier con respecto a t es

$${\ displaystyle \ mathbf {B} '' (t) = 6 (1-t) (\ mathbf {P} _ {2} -2 \ mathbf {P} _ {1} + \ mathbf {P} _ {0 }) + 6t (\ mathbf {P} _ {3} -2 \ mathbf {P} _ {2} + \ mathbf {P} _ {1}) \ ,.}

Definición general [ editar ]

Las curvas de Bézier se pueden definir para cualquier grado n.

Definición recursiva [ editar ]

Una definición recursiva para la curva de Bézier de grado n lo expresa como una combinación lineal punto a punto ( interpolación lineal ) de un par de puntos correspondientes en dos curvas de Bézier de grado n  - 1.

Dejar $${\ displaystyle \ mathbf {B} _ {\ mathbf {P} _ {0} \ mathbf {P} _ {1} \ ldots \ mathbf {P} _ {n}}}denota la curva de Bézier determinada por cualquier selección de puntos P ₀ , P ₁ , ...,  P _n . Entonces para empezar,

$${\ displaystyle \ mathbf {B} _ {\ mathbf {P} _ {0}} (t) = \ mathbf {P} _ {0} {\ text {, y}}}

$${\ displaystyle \ mathbf {B} (t) = \ mathbf {B} _ {\ mathbf {P} _ {0} \ mathbf {P} _ {1} \ ldots \ mathbf {P} _ {n}} ( t) = (1-t) \ mathbf {B} _ {\ mathbf {P} _ {0} \ mathbf {P} _ {1} \ ldots \ mathbf {P} _ {n-1}} (t) + t \ mathbf {B} _ {\ mathbf {P} _ {1} \ mathbf {P} _ {2} \ ldots \ mathbf {P} _ {n}} (t)}

Esta recursión se explica en las animaciones a continuación.

Definición explícita [ editar ]

La fórmula se puede expresar explícitamente de la siguiente manera:

{\ displaystyle {\ begin {alineado} \ mathbf {B} (t) & = \ sum _ {i = 0} ^ {n} {n \ elige i} (1-t) ^ {ni} t ^ {i } \ mathbf {P} _ {i} \\ & = (1-t) ^ {n} \ mathbf {P} _ {0} + {n \ elige 1} (1-t) ^ {n-1} t \ mathbf {P} _ {1} + \ cdots + {n \ elige n-1} (1-t) t ^ {n-1} \ mathbf {P} _ {n-1} + t ^ {n } \ mathbf {P} _ {n} && 0 \ leqslant t \ leqslant 1 \ end {alineado}}}

dónde $${\ displaystyle \ scriptstyle {n \ elige i}}Son los coeficientes binomiales .

Por ejemplo, para n  = 5:

{\ displaystyle {\ begin {alineado} \ mathbf {B} (t) & = (1-t) ^ {5} \ mathbf {P} _ {0} + 5t (1-t) ^ {4} \ mathbf {P} _ {1} + 10t ^ {2} (1-t) ^ {3} \ mathbf {P} _ {2} + 10t ^ {3} (1-t) ^ {2} \ mathbf {P } _ {3} + 5t ^ {4} (1-t) \ mathbf {P} _ {4} + t ^ {5} \ mathbf {P} _ {5} && 0 \ leqslant t \ leqslant 1 \ end { alineado}}}

Terminología [ editar ]

Alguna terminología está asociada con estas curvas paramétricas. Tenemos

$${\ displaystyle \ mathbf {B} (t) = \ sum _ {i = 0} ^ {n} b_ {i, n} (t) \ mathbf {P} _ {i}, \ quad 0 \ leq t \ leq 1}

donde los polinomios

$${\ displaystyle b_ {i, n} (t) = {n \ elige i} t ^ {i} (1-t) ^ {ni}, \ quad i = 0, \ ldots, n}

Son conocidos como polinomios de base Bernstein de grado n .

Tenga en cuenta que t ⁰  = 1, (1 -  t ) ⁰  = 1, y que el coeficiente binomial ,$${\ displaystyle \ scriptstyle {n \ elige i}}, expresado también como $${\ displaystyle ^ {n} {\ mathbf {C}} _ ​​{i}} o $${\ displaystyle {\ mathbf {C}} _ ​​{i} ^ {n}}, es:

$${\ displaystyle {n \ elige i} = {\ frac {n!} {i! (ni)!}}}

Los puntos P _i se denominan puntos de control para la curva de Bézier. El polígono formado al conectar los puntos Bézier con líneas , comenzando con P ₀ y terminando con P _n , se llama polígono Bézier (o polígono de control ). El casco convexo del polígono de Bézier contiene la curva de Bézier.

Forma polinomial [ editar ]

A veces es deseable expresar la curva de Bézier como un polinomio en lugar de una suma de polinomios de Bernstein menos sencillos . La aplicación del teorema del binomio a la definición de la curva seguida por alguna reorganización dará como resultado:

$${\ displaystyle \ mathbf {B} (t) = \ sum _ {j = 0} ^ {n} {t ^ {j} \ mathbf {C} _ {j}}}

dónde

$${\ displaystyle \ mathbf {C} _ {j} = {\ frac {n!} {(nj)!}} \ sum _ {i = 0} ^ {j} {\ frac {(-1) ^ {i + j} \ mathbf {P} _ {i}} {i! (ji)!}} = \ prod _ {m = 0} ^ {j-1} (nm) \ sum _ {i = 0} ^ { j} {\ frac {(-1) ^ {i + j} \ mathbf {P} _ {i}} {i! (ji)!}}.}

Esto podría ser práctico si $${\ displaystyle \ mathbf {C} _ {j}} Se puede calcular antes de muchas evaluaciones de $${\ displaystyle \ mathbf {B} (t)}; sin embargo, se debe tener cuidado, ya que las curvas de orden alto pueden carecer de estabilidad numérica ( si esto ocurre, se debe usar el algoritmo de Casteljau ). Tenga en cuenta que el producto vacío es 1.

Propiedades [ editar ]

Una curva de Bézier cúbica (amarilla) se puede hacer idéntica a una cuadrática (negra) mediante

1. Copiando los puntos finales, y

2. Colocar sus 2 puntos de control medio (círculos amarillos) 2/3 a lo largo de los segmentos de línea desde los puntos finales hasta el punto de control medio de la curva cuadrática (rectángulo negro)

• La curva comienza en P ₀ y termina en P _n ; Esta es la llamada propiedad de interpolación de punto final .
• La curva es una línea recta si y solo si todos los puntos de control son colineales .
• El inicio y el final de la curva es tangente a la primera y última sección del polígono de Bézier, respectivamente.
• Una curva se puede dividir en cualquier punto en dos subcurves, o arbitrariamente en muchos subcurves, cada uno de los cuales es también una curva de Bézier.
• Algunas curvas que parecen simples, como el círculo , no se pueden describir exactamente mediante una curva de Bézier o de Bézier a trozos ; aunque una curva de Bézier cúbica de cuatro piezas puede aproximarse a un círculo (ver curva de Bézier compuesta ), con un error radial máximo de menos de una parte en mil, cuando cada punto de control interno (o punto fuera de línea) es la distancia$${\ displaystyle \ textstyle {\ frac {4 \ left ({\ sqrt {2}} - 1 \ right)} {3}}}horizontal o verticalmente desde un punto de control externo en un círculo unitario. Más generalmente, una curva Bézier cúbica de n piezas puede aproximarse a un círculo, cuando cada punto de control interno es la distancia$${\ displaystyle \ textstyle {\ frac {4} {3}} \ tan (t / 4)}desde un punto de control externo en un círculo unitario, donde t es 360 / n grados, y n > 2.
• Cada curva de Bézier cuadrática es también una curva de Bézier cúbica, y más generalmente, cada curva de Bézier de grado n es también una curva de grado m para cualquier m > n . En detalle, una curva de grado n con puntos de control P ₀ , ..., P _n es equivalente (incluida la parametrización) a la curva de grado n + 1 con puntos de control P ' ₀ , ..., P' _{n + 1} , donde$${\ displaystyle \ mathbf {P} '_ {k} = {\ tfrac {k} {n + 1}} \ mathbf {P} _ {k-1} + \ left (1 - {\ tfrac {k} { n + 1}} \ derecha) \ mathbf {P} _ {k}}.
• Las curvas de Bézier tienen la variación disminuyendo la propiedad . Lo que esto significa en términos intuitivos es que las curvas de Bézier no "ondulan" más que el polígono de sus puntos de control, y en realidad pueden "ondular" menos que eso. ^[12]
• No hay control local en las curvas de Bézier de grado n , lo que significa que cualquier cambio en un punto de control requiere un nuevo cálculo y, por lo tanto, afecta el aspecto de toda la curva ", aunque cuanto más lejos esté uno del punto de control que se cambió, más pequeño es El cambio en la curva ". ^[13]

Curva de segundo orden es un segmento parabólico [ editar ]

Equivalencia de una curva de Bézier cuadrática y un segmento parabólico.

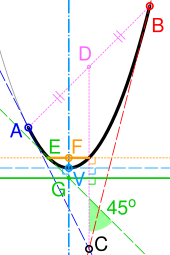
Una curva de Bézier cuadrática es también un segmento de una parábola . Como una parábola es una sección cónica , algunas fuentes se refieren a los Béziers cuadráticos como "arcos cónicos". ^[10] Con referencia a la figura de la derecha, las características importantes de la parábola se pueden derivar de la siguiente manera: ^[14]

1. Las tangentes a la parábola en los puntos finales de la curva (A y B) se intersecan en su punto de control (C).
2. Si D es el punto medio de AB, la tangente a la curva que es perpendicular a CD (línea cian discontinua) define su vértice (V). Su eje de simetría (guión-punto cian) pasa a través de V y es perpendicular a la tangente.
3. E es cualquier punto en la curva con una tangente a 45 ° a CD (verde discontinuo). Si G es la intersección de esta tangente y el eje, la línea que pasa a través de G y perpendicular a CD es la directriz (verde continuo).
4. El foco (F) se encuentra en la intersección del eje y una línea que pasa por E y es perpendicular a CD (punto amarillo). El latus recto es el segmento de línea dentro de la curva (amarillo sólido).

Derivado [ editar ]

La derivada para una curva de orden n es

$${\ displaystyle \ mathbf {B} '(t) = n \ sum _ {i = 0} ^ {n-1} b_ {i, n-1} (t) (\ mathbf {P} _ {i + 1 } - \ mathbf {P} _ {i})}

Construyendo curvas de Bézier [ editar ]

Curvas lineales [ editar ]

Se puede pensar que la t en la función para una curva de Bézier lineal describe la distancia a la que B ( t ) está desde P ₀ a P ₁ . Por ejemplo, cuando t = 0.25 , B ( t ) es un cuarto del camino desde el punto P ₀ hasta P ₁ . Como t varía de 0 a 1, B ( t ) describe una línea recta de P ₀ a P ₁ .

Animación de una curva de Bézier lineal, t en [0,1]

Curvas cuadráticas [ editar ]

Para las curvas de Bézier cuadráticas, se pueden construir los puntos intermedios Q ₀ y Q _{1, de} modo que t varía de 0 a 1:

• El punto Q ₀ ( t ) varía de P ₀ a P ₁ y describe una curva de Bézier lineal.
• El punto Q ₁ ( t ) varía de P ₁ a P ₂ y describe una curva de Bézier lineal.
• El punto B ( t ) se interpola linealmente entre Q ₀ ( t ) y Q ₁ ( t ) y describe una curva de Bézier cuadrática.

Construcción de una curva cuadrática de Bézier.		Animación de una curva de Bézier cuadrática, t en [0,1]

Curvas de orden superior [ editar ]

Para las curvas de orden superior, se necesitan más puntos intermedios. Para las curvas cúbicas, se pueden construir puntos intermedios Q ₀ , Q ₁ y Q ₂ que describen curvas lineales de Bézier, y puntos R ₀ y R ₁ que describen curvas cuadráticas de Bézier:

Construcción de una curva cúbica de Bézier.		Animación de una curva de Bézier cúbica, t en [0,1]

Para curvas de cuarto orden se pueden construir puntos intermedios Q ₀ , Q ₁ , Q ₂ y Q ₃ que describen curvas lineales de Bézier, puntos R ₀ , R ₁ y R ₂ que describen curvas cuadráticas de Bézier y puntos S ₀ y S ₁ que Describe las curvas cúbicas de Bézier:

Construcción de una curva de Bézier quártica.		Animación de una curva de Bézier quartic, t en [0,1]

Para las curvas de quinto orden, se pueden construir puntos intermedios similares.

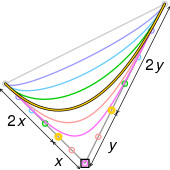
Animación de una curva de Bézier de quinto orden, t en [0,1] en rojo. También se muestran las curvas de Bézier para cada uno de los órdenes inferiores.

Estas representaciones se basan en el proceso utilizado en el algoritmo de De Casteljau para calcular las curvas de Bézier. ^[15]

Desplazamientos (también conocidos como trazos) de las curvas de Bézier [ editar ]

La curva en un desplazamiento fijo de una curva de Bézier dada, denominada desviación o curva paralela en matemáticas (que se encuentra "paralela" a la curva original, como el desplazamiento entre rieles en una vía del ferrocarril ), no puede formarse exactamente mediante una curva de Bézier ( excepto en algunos casos triviales). En general, la curva de desplazamiento bilateral de un Bézier cúbico es una curva algebraica de décimo orden ^[16] y, más generalmente, para un Bézier de grado n, la curva de desplazamiento bilateral es una curva algebraica de grado 4 n -2. ^[17] Sin embargo, hay métodos heurísticos que generalmente dan una aproximación adecuada para propósitos prácticos. ^[18]

En el campo de los gráficos vectoriales , la pintura de dos curvas de desviación simétricamente distanciadas se denomina trazo (la curva de Bézier o, en general, una trayectoria de varios segmentos de Bézier). ^[16] La conversión de curvas de desplazamiento a contornos Bézier rellenos es de importancia práctica en la conversión de las fuentes definidas en METAFONT , que permite el trazo de las curvas de Bézier, a las fuentes PostScript tipo 1 más utilizadas , que solo permiten (por razones de eficiencia) las matemáticas Operación más simple de rellenar un contorno definido por curvas de Bézier (que no se intersectan por sí mismas). ^[19]

Grado de elevación [ editar ]

Una curva de Bézier de grado n se puede convertir en una curva de Bézier de grado n  + 1 con la misma forma . Esto es útil si el software admite curvas de Bézier solo de un grado específico. Por ejemplo, los sistemas que solo pueden trabajar con curvas de Bézier cúbicas pueden trabajar implícitamente con curvas cuadráticas utilizando su representación cúbica equivalente.

Para hacer la elevación del grado, utilizamos la igualdad. $${\ displaystyle \ mathbf {B} (t) = (1-t) \ mathbf {B} (t) + t \ mathbf {B} (t).} Cada componente $${\ displaystyle \ mathbf {b} _ {i, n} (t) \ mathbf {P} _ {i}}se multiplica por (1 -  t )  yt , aumentando así un grado en uno, sin cambiar el valor. Aquí está el ejemplo de grado creciente de 2 a 3.

{\ displaystyle {\ begin {alineado} (1-t) ^ {2} \ mathbf {P} _ {0} +2 (1-t) t \ mathbf {P} _ {1} + t ^ {2} \ mathbf {P} _ {2} & = (1-t) ^ {3} \ mathbf {P} _ {0} +2 (1-t) ^ {2} t \ mathbf {P} _ {1} + (1-t) t ^ {2} \ mathbf {P} _ {2} + (1-t) ^ {2} t \ mathbf {P} _ {0} +2 (1-t) t ^ { 2} \ mathbf {P} _ {1} + t ^ {3} \ mathbf {P} _ {2} \\ & = (1-t) ^ {3} \ mathbf {P} _ {0} + ( 1-t) ^ {2} t \ left (\ mathbf {P} _ {0} +2 \ mathbf {P} _ {1} \ right) + (1-t) t ^ {2} \ left (2 \ mathbf {P} _ {1} + \ mathbf {P} _ {2} \ right) + t ^ {3} \ mathbf {P} _ {2} \\ & = (1-t) ^ {3} \ mathbf {P} _ {0} +3 (1-t) ^ {2} t {\ tfrac {1} {3}} \ left (\ mathbf {P} _ {0} +2 \ mathbf {P} _ {1} \ derecha) +3 (1-t) t ^ {2} {\ tfrac {1} {3}} \ izquierda (2 \ mathbf {P} _ {1} + \ mathbf {P} _ { 2} \ derecha) + t ^ {3} \ mathbf {P} _ {2} \ end {alineado}}}

Para n arbitrarios utilizamos igualdades.

$${\ displaystyle {\ begin {cases} {n + 1 \ elige i} (1-t) \ mathbf {b} _ {i, n} = {n \ elige i} \ mathbf {b} _ {i, n +1} \\ {n + 1 \ elige i + 1} t \ mathbf {b} _ {i, n} = {n \ elige i} \ mathbf {b} _ {i + 1, n + 1} \ end {cases}} \ quad \ Rightarrow \ quad {\ begin {cases} (1-t) \ mathbf {b} _ {i, n} = {\ frac {n + 1-i} {n + 1}} \ mathbf {b} _ {i, n + 1} \\ t \ mathbf {b} _ {i, n} = {\ frac {i + 1} {n + 1}} \ mathbf {b} _ {i + 1, n + 1} \ end {cases}}}

Por lo tanto:

{\ displaystyle {\ begin {alineado} \ mathbf {B} (t) & = (1-t) \ sum _ {i = 0} ^ {n} \ mathbf {b} _ {i, n} (t) \ mathbf {P} _ {i} + t \ sum _ {i = 0} ^ {n} \ mathbf {b} _ {i, n} (t) \ mathbf {P} _ {i} \\ & = \ sum _ {i = 0} ^ {n} {\ frac {n + 1-i} {n + 1}} \ mathbf {b} _ {i, n + 1} (t) \ mathbf {P} _ {i} + \ sum _ {i = 0} ^ {n} {\ frac {i + 1} {n + 1}} \ mathbf {b} _ {i + 1, n + 1} (t) \ mathbf {P} _ {i} \\ & = \ sum _ {i = 0} ^ {n + 1} \ left ({\ frac {i} {n + 1}} \ mathbf {P} _ {i-1 } + {\ frac {n + 1-i} {n + 1}} \ mathbf {P} _ {i} \ right) \ mathbf {b} _ {i, n + 1} (t) \\ & = \ sum _ {i = 0} ^ {n + 1} \ mathbf {b} _ {i, n + 1} (t) \ mathbf {P '} _ {i} \ end {alineado}}}

introduciendo arbitrario $${\ displaystyle \ mathbf {P} _ {- 1}} y $${\ displaystyle \ mathbf {P} _ {n + 1}}.

Por lo tanto, los nuevos puntos de control son ^[20]

$${\ displaystyle \ mathbf {P '} _ {i} = {\ frac {i} {n + 1}} \ mathbf {P} _ {i-1} + {\ frac {n + 1-i} {n +1}} \ mathbf {P} _ {i}, \ quad i = 0, \ ldots, n + 1}

Grado de elevación repetida [ editar ]

El concepto de Elevación de grado se puede repetir en un polígono de control R para obtener una secuencia de polígonos de control R , R ₁ , R ₂ , etc. Después de las elevaciones de r grados, el polígono R _r tiene los vértices P _{0, r} , P _{1, r} , P _{2, r} , ..., P _{n + r, r} dados por ^[20]

$${\ displaystyle \ mathbf {P} _ {i, r} = \ sum _ {j = 0} ^ {n} \ mathbf {P} _ {j} {\ tbinom {n} {j}} {\ frac { \ tbinom {r} {ij}} {\ tbinom {n + r} {i}}}}

También se puede demostrar que para la curva B de Bézier subyacente ,

$${\ displaystyle \ mathbf {\ lim _ {r \ to \ infty} R_ {r}} = \ mathbf {B}}

Las curvas de Bézier racionales [ editar ]

Segmentos de secciones cónicas representadas exactamente por curvas de Bézier racionales

La curva racional de Bézier agrega pesos ajustables para proporcionar aproximaciones más cercanas a formas arbitrarias. El numerador es una curva de Bézier de forma de Bernstein ponderada y el denominador es una suma ponderada de polinomios de Bernstein . Las curvas Rational Bézier pueden, entre otros usos, ser usadas para representar segmentos de secciones cónicas exactamente, incluyendo arcos circulares. ^[21]

Dados n + 1 puntos de control P _i , la curva de Bézier racional se puede describir mediante:

$${\ displaystyle \ mathbf {B} (t) = {\ frac {\ sum _ {i = 0} ^ {n} b_ {i, n} (t) \ mathbf {P} _ {i} w_ {i} } {\ sum _ {i = 0} ^ {n} b_ {i, n} (t) w_ {i}}}}

o simplemente

$${\ displaystyle \ mathbf {B} (t) = {\ frac {\ sum _ {i = 0} ^ {n} {n \ elige i} t ^ {i} (1-t) ^ {ni} \ mathbf {P} _ {i} w_ {i}} {\ sum _ {i = 0} ^ {n} {n \ elige i} t ^ {i} (1-t) ^ {ni} w_ {i}} }.}