GEOMETRÍA ANALÍTICA - CURVAS

 bicorn , también conocido como una curva de sombrero abombado debido a su parecido con un bicorne , es una curva quártica racional definida por la ecuación.

$${\ displaystyle y ^ {2} (a ^ {2} -x ^ {2}) = (x ^ {2} + 2ay-a ^ {2}) ^ {2}.}

Tiene dos cúspides y es simétrica respecto al eje y.

Bicornio

Historia [ editar ]

En 1864, James Joseph Sylvester estudió la curva.

$${\ displaystyle y ^ {4} -xy ^ {3} -8xy ^ {2} + 36x ^ {2} y + 16x ^ {2} -27x ^ {3} = 0}

en relación con la clasificación de las ecuaciones quínticas ; llamó a la curva un bicorn porque tiene dos cúspides. Esta curva fue estudiada más a fondo por Arthur Cayley en 1867.

Propiedades [ editar ]

Un bicorn transformado con a = 1

El bicorn es una curva algebraica plana de grado cuatro y género cero. Tiene dos singularidades de cúspide en el plano real y un punto doble en el plano proyectivo complejo en x = 0, z = 0. Si movemos x = 0 y z = 0 al origen sustituyendo y realizamos una rotación imaginaria en x bu sustituyendo ix / z por x y 1 / z por y en la curva bicorn, obtenemos

$${\ displaystyle (x ^ {2} -2az + a ^ {2} z ^ {2}) ^ {2} = x ^ {2} + a ^ {2} z ^ {2}. \,}

Esta curva, un limaçon , tiene un punto doble ordinario en el origen, y dos nodos en el plano complejo, en x = ± i y z = 1.

Las ecuaciones paramétricas de una curva bicorn son:

$${\ displaystyle x = a \ sin (\ theta)} y $${\ displaystyle y = a {\ frac {\ cos ^ {2} (\ theta) \ left (2+ \ cos (\ theta) \ right)} {3+ \ sin ^ {2} (\ theta)}} } con $${\ displaystyle - \ pi \ leq \ theta \ leq \ pi}

Un bifolio es una curva de plano quárticodibujada en un plano a través de la ecuación

$${\ displaystyle (x ^ {2} + y ^ {2}) ^ {2} = ax ^ {2} y.}

Construcción y ecuaciones [ editar ]

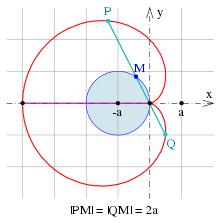
Dado un círculo C a través de un punto O, y la línea L tangente al círculo en el punto O: para cada punto Q en C, defina el punto P tal que PQ sea paralelo a la línea tangente L, y PQ = OQ. La colección de puntos P forma el bifolio. ^[1]

En coordenadas polares , la ecuación del bifolio es

$${\ displaystyle \ rho = a \ sin \ theta \ cos ^ {2} \ theta.}

Para un = 1, el total incluido área es de aproximadamente 0,10.

Construcción del Bifolio.

Bifolium para a = 1.

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Curva de punta de bala con a = 1 y b= 1

En matemáticas , una curva de punta de bala es una curva cuártica unicursal con tres puntos de inflexión , dada por la ecuación

$${\ displaystyle a ^ {2} y ^ {2} -b ^ {2} x ^ {2} = x ^ {2} y ^ {2} \,}

La curva de la bala tiene tres puntos dobles en el plano proyectivo real , en x = 0 e y = 0, x = 0 y z = 0, y y = 0 y z = 0, y por lo tanto es una curva unicursal (racional) del género. cero.

Si

$${\ displaystyle f (z) = \ sum _ {n = 0} ^ {\ infty} {2n \ elegir n} z ^ {2n + 1} = z + 2z ^ {3} + 6z ^ {5} + 20z ^ {7} + \ cdots}

entonces

$${\ displaystyle y = f \ left ({\ frac {x} {2a}} \ right) \ pm 2b \}

Son las dos ramas de la curva de la bala en el origen.

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Una construcción animada da una idea de la complejidad de la curva ( haga clic para obtener una versión ampliada ).

La curva de la mariposa.

La curva de mariposa es una curva de plano trascendental descubierta por el Templo H. Fay . La curva está dada por las siguientes ecuaciones paramétricas:

$${\ displaystyle x = \ sin (t) \ left (e ^ {\ cos (t)} - ​​2 \ cos (4t) - \ sin ^ {5} \ left ({t \ over 12} \ right) \ right )}

$${\ displaystyle y = \ cos (t) \ left (e ^ {\ cos (t)} - ​​2 \ cos (4t) - \ sin ^ {5} \ left ({t \ over 12} \ right) \ right )}

$${\ displaystyle 0 \ leq t \ leq 12 \ pi}

o por la siguiente ecuación polar :

$${\ displaystyle r = e ^ {\ sin \ theta} -2 \ cos (4 \ theta) + \ sin ^ {5} \ left ({\ frac {2 \ theta - \ pi} {24}} \ right) }

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Cardioide generado por un círculo rodante en un círculo con el mismo radio

Un cardioide (del καρδία griego "corazón") es una curva plana trazada por un punto en el perímetro de un círculo que gira alrededor de un círculo fijo del mismo radio. También se puede definir como un epicicloide que tiene una sola cúspide . También es un tipo de espiral sinusoidal y una curva inversa de la parábola con el foco como centro de inversión. ^[1]

El nombre fue acuñado por de Castillon en 1741 ^[2], pero había sido objeto de estudio décadas antes. ^[3] Llamado así por su forma de corazón, tiene la forma más parecida al contorno de la sección transversal de una manzana redonda sin el tallo.

Un micrófono cardioide muestra un patrón de captación acústica que, cuando se grafica en dos dimensiones, se asemeja a un cardioide (cualquier plano 2d que contiene la línea recta 3d del cuerpo del micrófono). En tres dimensiones, el cardioide tiene la forma de una manzana centrada alrededor del micrófono. que es el "tallo" de la manzana.

Ecuaciones [ editar ]

Generación de un cardioide y el sistema de coordenadas utilizado.

Dejar $${\ displaystyle a} Ser el radio común de los dos círculos generadores con puntos medios. $${\ displaystyle (-a, 0), (a, 0)}, $${\ displaystyle \ varphi}el ángulo de rodadura y el origen el punto de inicio (ver imagen). Uno obtiene el

• Representación paramétrica :

$${\ displaystyle x (\ varphi) = 2a (1- \ cos \ varphi) \ cdot \ cos \ varphi \,}

{\ displaystyle y (\ varphi) = 2a (1- \ cos \ varphi) \ cdot \ sin \ varphi \, \ qquad 0 \ leq \ varphi <2 font="" pi="">

y la representación en

• coordenadas polares :

$${\ displaystyle r (\ varphi) = 2a (1- \ cos \ varphi)}.

Introduciendo las sustituciones. $${\ displaystyle \ cos \ varphi = x / r} y $${\ displaystyle r = {\ sqrt {x ^ {2} + y ^ {2}}}} uno obtiene después de eliminar la raíz cuadrada la representación implícita en

• coordenadas cartesianas :

$${\ displaystyle (x ^ {2} + y ^ {2}) ^ {2} + 4ax (x ^ {2} + y ^ {2}) - 4a ^ {2} y ^ {2} \, = \ , 0} .

Prueba de la representación paramétrica.

La prueba se puede hacer fácilmente utilizando números complejos y su descripción común como plano complejo. El movimiento de rodadura del círculo negro sobre el azul se puede dividir en dos rotaciones. En el plano complejo una rotación alrededor del punto.$${\ displaystyle 0} (origen) por un ángulo $${\ displaystyle \ varphi} Se puede realizar mediante la multiplicación de un punto. $${\ displaystyle z} (número complejo) por $${\ displaystyle e ^ {i \ varphi}}. Por lo tanto, la

rotación $${\ displaystyle \ Phi _ {+}} alrededor del punto $${\ displaystyle a} es$${\ displaystyle: \ quad z \ mapsto \ quad a + (za) e ^ {i \ varphi}},

rotación $${\ displaystyle \ Phi _ {-}} alrededor del punto $${\ displaystyle -a} es: $${\ displaystyle z \ mapsto -a + (z + a) e ^ {i \ varphi}}.

Un punto $${\ displaystyle p (\ varphi)} del cardioide se genera girando el origen alrededor del punto $${\ displaystyle a} y posterior rotación alrededor $${\ displaystyle -a}por el mismo ángulo $${\ displaystyle \ varphi}:

$${\ displaystyle p (\ varphi) = \ Phi _ {-} (\ Phi _ {+} (0)) = \ Phi _ {-} (a-ae ^ {i \ varphi}) = - a + (a- ae ^ {i \ varphi} + a) e ^ {i \ varphi} = a \; (- e ^ {i2 \ varphi} + 2e ^ {i \ varphi} -1)}.

De aquí se obtiene la representación paramétrica arriba:

{\ displaystyle {\ begin {array} {cclcccc} x (\ varphi) & = & a \; (- \ cos (2 \ varphi) +2 \ cos \ varphi -1) & = & 2a (1- \ cos \ varphi ) \ cdot \ cos \ varphi && \\ y (\ varphi) & = & a \; (- \ sin (2 \ varphi) +2 \ sin \ varphi) & = & 2a (1- \ cos \ varphi) \ cdot \ sin \ varphi &. & \ end {array}}}

(Las siguientes fórmulas $${\ displaystyle e ^ {i \ varphi} = \ cos \ varphi + i \ sin \ varphi, \ (\ cos \ varphi) ^ {2} + (\ sin \ varphi) ^ {2} = 1, \ \ cos 2 \ varphi = (\ cos \ varphi) ^ {2} - (\ sin \ varphi) ^ {2}, \; \ sin 2 \ varphi = 2 \ sin \ varphi \ cos \ varphi}fueron usados. Ver funciones trigonométricas .

Propiedades métricas [ editar ]

Para el cardioide como se definió anteriormente, las siguientes fórmulas contienen:

• zona $${\ displaystyle A = 6 \ pi a ^ {2}},
• longitud de arco $${\ displaystyle L = 16a} y
• radio de curvatura $${\ displaystyle \ rho (\ varphi) = {\ tfrac {8} {3}} a \ sin {\ tfrac {\ varphi} {2}} \.}

Las pruebas de esta declaración utilizan en ambos casos la representación polar del cardioide. Para las fórmulas adecuadas, consulte el sistema de coordenadas polares (longitud del arco) y el sistema de coordenadas polares (área)

prueba de la fórmula del área

$${\ displaystyle A = 2 \ cdot {\ tfrac {1} {2}} \ int _ {0} ^ {\ pi} {(r (\ varphi)) ^ {2}} \; d \ varphi = \ int _ {0} ^ {\ pi} {4a ^ {2} (1- \ cos \ varphi) ^ {2}} \; d \ varphi = \ cdots = 4a ^ {2} \ cdot {\ tfrac {3} {2}} \ pi = 6 \ pi a ^ {2}} .

prueba de la fórmula de longitud de arco

$${\ displaystyle L = 2 \ int _ {0} ^ {\ pi} {\ sqrt {r (\ varphi) ^ {2} + (r '(\ varphi)) ^ {2}}} \; d \ varphi = \ cdots = 8a \ int _ {0} ^ {\ pi} {\ sqrt {{\ tfrac {1} {2}} (1- \ cos \ varphi)}} \; d \ varphi = 8a \ int _ {0} ^ {\ pi} \ sin ({\ tfrac {\ varphi} {2}}) d \ varphi = 16a} .

prueba del radio de curvatura

El radio de curvatura. $${\ displaystyle \ rho} de una curva en coordenadas polares con ecuación $${\ displaystyle r = r (\ varphi)}es (s. curvatura )

$${\ displaystyle \ rho (\ varphi) = {\ frac {\ left [r (\ varphi) ^ {2} + {\ dot {r}} (\ varphi) ^ {2} \ right] ^ {3/2 }} {r (\ varphi) ^ {2} +2 {\ dot {r}} (\ varphi) ^ {2} -r (\ varphi) {\ ddot {r}} (\ varphi)}} \. }

Para el cardioide $${\ displaystyle r (\ varphi) = 2a (1- \ cos \ varphi) = 4a \ sin ^ {2} {\ tfrac {\ varphi} {2}}} uno obtiene

$${\ displaystyle \ rho (\ varphi) = \ cdots = {\ frac {[16a ^ {2} \ sin ^ {2} {\ frac {\ varphi} {2}}] ^ {\ frac {3} {2 }}} {24a ^ {2} \ sin ^ {2} {\ frac {\ varphi} {2}}}} = {\ frac {8} {3}} a \ sin {\ frac {\ varphi} { 2}} \.}

Propiedades de un cardioide [ editar ]

Acordes de un cardioide

Acordes a través de la cúspide [ editar ]

• C1: los acordes a través de la cúspide del cardioide tienen la misma longitud$${\ displaystyle 4a} .
• C2: Los puntos medios de los acordes a través de la cúspide se encuentran en el perímetro del círculo del generador fijo (ver imagen).

prueba de C1

Los puntos $${\ displaystyle P: p (\ varphi), \; Q: p (\ varphi + \ pi)}están en un acorde a través de la cúspide (= origen). Por lo tanto

$${\ displaystyle | PQ | = r (\ varphi) + r (\ varphi + \ pi)}

$${\ displaystyle = 2a (1- \ cos \ varphi) + 2a (1- \ cos (\ varphi + \ pi)) = \ cdots = 4a} .

prueba de C2

Para la prueba se usa la representación en el plano complejo (ver arriba). Por los puntos

$${\ displaystyle P: \ p (\ varphi) = a \; (- e ^ {i2 \ varphi} + 2e ^ {i \ varphi} -1)}

$${\ displaystyle Q: \ p (\ varphi + \ pi) = a \; (- e ^ {i2 (\ varphi + \ pi)} + 2e ^ {i (\ varphi + \ pi)} - 1) = a \; (- e ^ {i2 \ varphi} -2e ^ {i \ varphi} -1)},

el punto medio del acorde $${\ displaystyle PQ} es

$${\ displaystyle M: ​​\ {\ tfrac {1} {2}} (p (\ varphi) + p (\ varphi + \ pi)) = \ cdots = -a-ae ^ {i2 \ varphi}}

que se encuentra en el perímetro del círculo con el punto medio $${\ displaystyle -a} y radio $${\ displaystyle a} (ver foto).

Cardioide como curva inversa de una parábola [ editar ]

cardioide generado por la inversión de una parábola a través del círculo unitario (discontinua)

Articulo principal: geometría inversiva.

• Un cardioide es la curva inversa de una parábola con su enfoque en el centro de inversión (ver gráfico)

Para el ejemplo que se muestra en la gráfica, los círculos generadores tienen un radio $${\ displaystyle a = {\ tfrac {1} {2}}}. De ahí que el cardioide tenga la representación polar.

$${\ displaystyle r (\ varphi) = 1- \ cos \ varphi}

y su curva inversa

$${\ displaystyle r (\ varphi) = {\ frac {1} {1- \ cos \ varphi}}},

que es una parábola (s. parábola en coordenadas polares ) con la ecuación$${\ displaystyle x = {\ tfrac {1} {2}} (y ​​^ {2} -1)} En coordenadas cartesianas.

Observación: No todas las curvas inversas de una parábola son cardioides. Por ejemplo, si una parábola se invierte a través de un círculo cuyo centro se encuentra en el vértice de la parábola, el resultado es un cissoide de Diocles .

Cardioide como sobre de un lápiz de círculos [ editar ]

Cardioide como sobre de un lápiz de círculos.

En la sección anterior, si uno invierte adicionalmente las tangentes de la parábola, obtiene un lápiz de círculos a través del centro de la inversión (origen). Una consideración detallada muestra: Los puntos medios de los círculos se encuentran en el perímetro del círculo del generador fijo. (El círculo generador es la curva inversa de la directriz de las parábolas).

Esta propiedad da lugar al siguiente método simple para dibujar un cardioide:

1) Elige un círculo $${\ displaystyle c} y un punto $${\ displaystyle O} en su perímetro,

2) dibujar círculos que contengan $${\ displaystyle O} con centros en $${\ displaystyle c}y

3) Dibuja el sobre de estos círculos.

prueba con la condición del sobre

El sobre del lápiz de curvas dado implícitamente.

$${\ displaystyle F (x, y, t) = 0}

con parametro $${\ displaystyle t} consiste en tales puntos $${\ displaystyle (x, y)} Cuales son las soluciones del sistema no lineal.

• $${\ displaystyle F (x, y, t) = 0, \ quad F_ {t} (x, y, t) = 0 \}( condición del sobre ).

($${\ displaystyle F_ {t}}Significa la derivada parcial para parámetro. $${\ displaystyle t}.

Dejar $${\ displaystyle c} sé el círculo con el punto medio $${\ displaystyle (-1,0)} y radio $${\ displaystyle 1}. Entonces$${\ displaystyle c} tiene representación paramétrica $${\ displaystyle (-1+ \ cos t, \ sin t)}. El lápiz de círculos con centro en$${\ displaystyle c} punto que contiene $${\ displaystyle O = (0,0)} puede ser representado implícitamente por

$${\ displaystyle F (x, y, t) = (x + 1- \ cos t) ^ {2} + (y- \ sin t) ^ {2} - (2-2 \ cos t) = 0},

que es equivalente a

$${\ displaystyle F (x, y, t) = x ^ {2} + y ^ {2} + 2x \; (1- \ cos t) -2y \; \ sin t = 0 \ ;.}

La segunda condición del sobre es

$${\ displaystyle F_ {t} (x, y, t) = 2x \; \ sin t-2y \; \ cos t = 0}.

Se comprueba fácilmente que los puntos del cardioide con la representación paramétrica.

$${\ displaystyle x (t) = 2 (1- \ cos t) \ cos t, \ quad y (t) = 2 (1- \ cos t) \ sin t}

cumplir con el sistema no lineal anterior. El parámetro$${\ displaystyle t} Es idéntico al parámetro de ángulo del cardioide.

Cardioide como sobre de un lápiz de líneas [ editar ]

Cardioide como sobre de un lápiz de líneas.

Un método similar y simple para dibujar un cardioide usa un lápiz de líneas . Se debe a L. Cremona :

1. Dibuja un círculo, divide su perímetro en partes espaciadas iguales con $${\ displaystyle 2N} Puntos (s. imagen) y numéralas consecutivamente.
2. Dibuja los acordes: $${\ displaystyle (1,2), (2,4), ...., (n, 2n), ...., (N, 2N), (N + 1,2), (N + 2, 4), ....,}. (Es decir: el segundo punto se mueve por velocidad doble).
3. El sobre de estos acordes es un cardioide.

La generación de un cardioide de Cremona.

prueba

La siguiente consideración utiliza fórmulas trigonométricas para $${\ displaystyle \ cos \ alpha + \ cos \ beta, \ \ sin \ alpha + \ sin \ beta, \ 1+ \ cos 2 \ alpha, \ \ cos 2 \ alpha, \ sin 2 \ alpha}. Para mantener los cálculos simples, se proporciona una prueba para el cardioide con representación polar $${\ displaystyle r = 2 (1 {\ color {rojo} +} \ cos \ varphi)}(Ver apartado Cardioides en diferentes posiciones ).

ecuación de la tangente

del cardioide con representación polar$${\ displaystyle r = 2 (1+ \ cos \ varphi)}:

De la representación paramétrica.

$${\ displaystyle x (\ varphi) = 2 (1+ \ cos \ varphi) \ cos \ varphi,}

$${\ displaystyle y (\ varphi) = 2 (1+ \ cos \ varphi) \ sin \ varphi}

uno obtiene el vector normal $${\ displaystyle {\ vec {n}} = ({\ dot {y}}, - {\ dot {x}}) ^ {T}}. La ecuación de la tangente.$${\ displaystyle {\ dot {y}} (\ varphi) \ cdot (xx (\ varphi)) - {\ dot {x}} (\ varphi) \ cdot (yy (\ varphi)) = 0} es:

$${\ displaystyle (\ cos 2 \ varphi + \ cos \ varphi) \ cdot x \ + \ (\ sin 2 \ varphi + \ sin \ varphi) \ cdot y = 2 (1+ \ cos \ varphi) ^ {2} \.}

Con ayuda de fórmulas trigonométricas y subsiguiente división por. $${\ displaystyle \ cos {\ tfrac {1} {2}} \ varphi}, la ecuación de la tangente se puede reescribir como:

• {\ displaystyle \ cos ({\ tfrac {3} {2}} \ varphi) \ cdot x + \ sin ({\ tfrac {3} {2}} \ varphi) \ cdot y = 4 (\ cos {\ tfrac { 1} {2}} \ varphi) ^ {3} \ quad 0 <\ varphi <2 font="" neq="" pi.="" pi="" varphi="">

ecuación del acorde

del circulo con punto medio$${\ displaystyle (1,0)} y radio $${\ displaystyle 3}: Para la ecuación de la línea secante que pasa los dos puntos. $${\ displaystyle (1 + 3 \ cos \ theta, 3 \ sin \ theta), \ (1 + 3 \ cos {\ color {rojo} 2} \ theta, 3 \ sin {\ color {rojo} 2} \ theta ))} uno obtiene:

$${\ displaystyle (\ sin \ theta - \ sin 2 \ theta) \ cdot x \ + \ (\ cos 2 \ theta - \ sin \ theta) \ cdot y = -2 \ cos \ theta - \ sin 2 \ theta \ .}

Con ayuda de fórmulas trigonométricas y la subsiguiente división por $${\ displaystyle \ sin {\ tfrac {1} {2}} \ theta} La ecuación de la línea secante puede ser reescrita por:

• {\ displaystyle \ cos ({\ tfrac {3} {2}} \ theta) \ cdot x + \ sin ({\ tfrac {3} {2}} \ theta) \ cdot y = 4 (\ cos {\ tfrac { 1} {2}} \ theta) ^ {3} \ quad 0 <\ theta <2 font="" pi.="">

A pesar de los dos ángulos $${\ displaystyle \ varphi, \ theta} tienen diferentes significados (foto) uno obtiene para $${\ displaystyle \ varphi = \ theta}la misma linea Por lo tanto, cualquier línea secante del círculo, definida anteriormente, también es una tangente del cardioide:

• El cardioide es el sobre de los acordes de un círculo.

Observación:
La prueba se puede realizar con la ayuda de las condiciones del sobre (vea la sección anterior) de un lápiz de curvas implícito:

$${\ displaystyle F (x, y, t) = \ cos {\ tfrac {3} {2}} t \ cdot x \ + \ \ sin {\ tfrac {3} {2}} t \ cdot y-4 ( \ cos {\ tfrac {1} {2}} t) ^ {3} = 0 \} es el lápiz de las líneas secantes de un círculo (s. arriba) y

$${\ displaystyle F_ {t} (x, y, t) = - {\ tfrac {3} {2}} \ sin {\ tfrac {3} {2}} t \ cdot x \ + \ {\ tfrac {3 } {2}} \ cos {\ tfrac {3} {2}} t \ cdot y + 3 \ cos {\ tfrac {1} {2}} t \ sin t = 0 \.}

Para el parámetro fijo t, ambas ecuaciones representan líneas. Su punto de intersección es

$${\ displaystyle x (t) = 2 (1+ \ cos t) \ cos t, \ quad y (t) = 2 (1+ \ cos t) \ sin t},

El cual es un punto del cardioide con ecuación polar. $${\ displaystyle r = 2 (1+ \ cos t).}

Cardioide como cáustico : fuente de luz$${\ displaystyle Z}, rayo de luz $${\ displaystyle {\ vec {s}}}rayo reflejado $${\ displaystyle {\ vec {r}}}

Cardioide como cáustico de un círculo con fuente de luz (derecha) en el perímetro

Cardioide como cáustico de un círculo [ editar ]

Las consideraciones hechas en la sección anterior dan una prueba del hecho de que la cáustica de un círculo con una fuente de luz en el perímetro del círculo es un cardioide.

• Si en el plano hay una fuente de luz. $${\ displaystyle Z} En el perímetro de un círculo que está reflejando cualquier rayo, entonces los rayos reflejados dentro del círculo son tangentes de un cardioide.

prueba

Como en la sección anterior, el círculo puede tener un punto medio. $${\ displaystyle (1,0)} y radio $${\ displaystyle 3}. Su representación paramétrica es.

$${\ displaystyle c (\ varphi) = (1 + 3 \ cos \ varphi, 3 \ sin \ varphi) \.}

La tangente en el punto del círculo. $${\ displaystyle C: \ k (\ varphi)} tiene vector normal $${\ displaystyle {\ vec {n}} _ {t} = (\ cos \ varphi, \ sin \ varphi) ^ {T}}. De ahí que el rayo reflejado tenga el vector normal.$${\ displaystyle {\ vec {n}} _ {r} = (\ cos {\ color {red} {\ tfrac {3} {2}}} \ varphi, \ sin {\ color {red} {\ tfrac { 3} {2}}} \ varphi) ^ {T}} (ver gráfico) y contiene punto $${\ displaystyle C: \ (1 + 3 \ cos \ varphi, 3 \ sin \ varphi)}. El rayo reflejado es parte de la línea con la ecuación (ver la sección anterior)

$${\ displaystyle \ cos {\ tfrac {3} {2}} \ varphi \ cdot x \ + \ \ sin {\ tfrac {3} {2}} \ varphi \ cdot y = 4 (\ cos {\ tfrac {1 } {2}} \ varphi) ^ {3} \,}

La cual es tangente del cardioide con ecuación polar.

$${\ displaystyle r = 2 (1+ \ cos \ varphi)}

de la sección anterior.

Observación: Para tales consideraciones, por lo general se descuidan las reflexiones múltiples en el círculo.

Cardioide como pedal de curva de un círculo [ editar ]

El punto de cardioide es el pie de la perpendicular caída sobre la tangente del círculo

La generación Cremona de un cardioide no debe confundirse con la siguiente generación:

Permitir $${\ displaystyle k} un circulo y $${\ displaystyle O}Un punto en el perímetro de este círculo. Lo siguiente es cierto:

• Los pies de las perpendiculares del punto. $${\ displaystyle O} en las tangentes del circulo $${\ displaystyle k} Son puntos de un cardioide.

Por lo tanto, un cardioide es una curva de pedal especial de un círculo.

prueba

En un círculo de sistema de coordenadas cartesiano. $${\ displaystyle k} puede tener punto medio $${\ displaystyle (2a, 0)} y radio $${\ displaystyle 2a}. La tangente en el punto del círculo.$${\ displaystyle (2a + 2a \ cos \ varphi, 2a \ sin \ varphi)} tiene la ecuación

$${\ displaystyle (x-2a) \ cdot \ cos \ varphi + y \ cdot \ sin \ varphi = 2a \.}

El pie de la perpendicular desde el punto. $${\ displaystyle O} en la tangente es punto $${\ displaystyle (r \ cos \ varphi, r \ sin \ varphi)} con la distancia aún desconocida $${\ displaystyle r} al origen $${\ displaystyle O}. Insertando el punto en la ecuación de los rendimientos tangentes.

$${\ displaystyle (r \ cos \ varphi -2a) \ cos \ varphi + r \ sin ^ {2} \ varphi = 2a \ quad \ rightarrow \ quad r = 2a (1+ \ cos \ varphi)}

que es la ecuación polar de un cardioide.

Observación: si punto$${\ displaystyle O} no está en el perímetro del círculo $${\ displaystyle k}, se consigue una limaçon de pascal .

La evolución de un cardioide [ editar ]

Evolución de un 
magenta cardioide : un punto P, su centro de curvatura M y su círculo oscilante

La evolución de una curva es el lugar de los centros de curvatura. En detalle: Para una curva.$${\ displaystyle {\ vec {x}} (s) = {\ vec {c}} (s)} con radio de curvatura $${\ displaystyle \ rho (s)} El evolucionado tiene la representación.

$${\ displaystyle {\ vec {X}} (s) = {\ vec {c}} (s) + \ rho (s) {\ vec {n}} (s).

con $${\ displaystyle {\ vec {n}} (s)} La unidad adecuadamente orientada normal.

Para un cardioide se obtiene:

• La evolución de un cardioide es otro cardioide de un tercio de grande (s. Imagen).

prueba

Para el cardioide con representación paramétrica.

$${\ displaystyle x (\ varphi) = 2a (1- \ cos \ varphi) \ cos \ varphi = 4a \ sin ^ {2} {\ tfrac {\ varphi} {2}} \ cos \ varphi \,}

$${\ displaystyle y (\ varphi) = 2a (1- \ cos \ varphi) \ sin \ varphi = 4a \ sin ^ {2} {\ tfrac {\ varphi} {2}} \ sin \ varphi}

la unidad normal es

$${\ displaystyle {\ vec {n}} (\ varphi) = (- \ sin {\ tfrac {3} {2}} \ varphi, \ cos {\ tfrac {3} {2}} \ varphi)}

y el radio de curvatura

$${\ displaystyle \ rho (\ varphi) = {\ tfrac {8} {3}} a \ sin {\ tfrac {\ varphi} {2}} \.}

De ahí que las ecuaciones paramétricas de la evolución sean

$${\ displaystyle X (\ varphi) = 4a \ sin ^ {2} {\ tfrac {\ varphi} {2}} \ cos \ varphi - {\ tfrac {8} {3}} a \ sin {\ tfrac {\ varphi} {2}} \ cdot \ sin {\ tfrac {3} {2}} \ varphi = \ cdots = {\ tfrac {4} {3}} a \ cos ^ {2} {\ tfrac {\ varphi} {2}} \ cos \ varphi - {\ tfrac {4} {3}} a \,}

$${\ displaystyle Y (\ varphi) = 4a \ sin ^ {2} {\ tfrac {\ varphi} {2}} \ sin \ varphi + {\ tfrac {8} {3}} a \ sin {\ tfrac {\ varphi} {2}} \ cdot \ cos {\ tfrac {3} {2}} \ varphi \ = \ cdots = {\ tfrac {4} {3}} a \ cos ^ {2} {\ tfrac {\ varphi } {2}} \ sin \ varphi \.}

Estas ecuaciones describen un cardioide un tercio como grande, girado 180 grados y desplazado a lo largo del eje x en $${\ displaystyle - {\ tfrac {4} {3}} a}.

(Se utilizaron fórmulas trigonométricas: $${\ displaystyle \ sin {\ tfrac {3} {2}} \ varphi = \ sin {\ tfrac {\ varphi} {2}} \ cos \ varphi + \ cos {\ tfrac {\ varphi} {2}} \ sin \ varphi \, \ \ cos {\ tfrac {3} {2}} \ varphi = \ cdots, \ \ sin \ varphi = 2 \ sin {\ tfrac {\ varphi} {2}} \ cos {\ tfrac { \ varphi} {2}} \, \ \ cos \ varphi = \ cdots \.})

Trayectorias ortogonales [ editar ]

cardioides ortogonales

Una trayectoria ortogonal de un lápiz de curvas es una curva que intersecta ortogonalmente cualquier curva del lápiz. Para cardioides se cumple lo siguiente:

• Las trayectorias ortogonales del lápiz de cardioides con ecuaciones.

{\ displaystyle r = 2a (1- \ cos \ varphi) \, \; a> 0 \, \}

son los cardioides con ecuaciones

{\ displaystyle r = 2b (1+ \ cos \ varphi) \, \; b> 0 \.}

(El segundo lápiz puede considerarse como reflejos en el eje y del primero. Vea el diagrama).

Prueba:
Para una curva dada en coordenadas polares por una función.$${\ displaystyle r (\ varphi)} Se mantiene la siguiente conexión a coordenadas cartesianas:

$${\ displaystyle x (\ varphi) = r (\ varphi) \ cos \ varphi \, \ qquad} $${\ displaystyle y (\ varphi) = r (\ varphi) \ sin \ varphi \ qquad}

y para los derivados.

$${\ displaystyle {\ frac {dx} {d \ varphi}} = r '(\ varphi) \ cos \ varphi -r (\ varphi) \ sin \ varphi \, \ qquad}$${\ displaystyle {\ frac {dy} {d \ varphi}} = r '(\ varphi) \ sin \ varphi + r (\ varphi) \ cos \ varphi \.}

Al dividir la segunda ecuación por la primera, se obtiene la pendiente cartesiana de la línea tangente a la curva en el punto $${\ displaystyle (r (\ varphi), \ varphi)}:

$${\ displaystyle {\ frac {dy} {dx}} = {\ frac {r '(\ varphi) \ sin \ varphi + r (\ varphi) \ cos \ varphi} {r' (\ varphi) \ cos \ varphi -r (\ varphi) \ sin \ varphi}}.}

Para los cardioides con las ecuaciones. $${\ displaystyle r = 2a (1- \ cos \ varphi) \;} y $${\ displaystyle r = 2b (1+ \ cos \ varphi) \} respectivamente se obtiene:

$${\ displaystyle {\ frac {dy_ {a}} {dx}} = {\ frac {\ cos \ varphi - \ cos 2 \ varphi} {\ sin 2 \ varphi - \ sin \ varphi}} \ quad} y $${\ displaystyle \ quad {\ frac {dy_ {b}} {dx}} = - {\ frac {\ cos \ varphi + \ cos 2 \ varphi} {\ sin 2 \ varphi + \ sin \ varphi}} \. }

(La pendiente de cualquier curva es dependiente de $${\ displaystyle \ varphi} Solo, y no a partir de los parámetros. $${\ displaystyle a, b} !) 
Por lo tanto

$${\ displaystyle {\ frac {dy_ {a}} {dx}} \ cdot {\ frac {dy_ {b}} {dx}} = \ cdots = - {\ frac {\ cos ^ {2} \ varphi - \ cos ^ {2} 2 \ varphi} {\ sin ^ {2} 2 \ varphi - \ sin ^ {2} \ varphi}} = - {\ frac {-1+ \ cos ^ {2} \ varphi + 1- \ cos ^ {2} 2 \ varphi} {\ sin ^ {2} 2 \ varphi - \ sin ^ {2} \ varphi}} = - 1 \.}

Eso significa que: cualquier curva del primer lápiz interseca con cualquier curva del segundo lápiz ortogonalmente.

4 cardioides en representación polar y su posición en el sistema de coordenadas

Cardioides en diferentes posiciones [ editar ]

La elección de otras posiciones del cardioide dentro del sistema de coordenadas da como resultado diferentes ecuaciones. La imagen muestra las 4 posiciones más comunes de un cardioide y sus ecuaciones polares.

Cardioides en análisis complejo [ editar ]

El límite de la bombilla central del conjunto de Mandelbrot es un cardioide.

En un análisis complejo , la imagen de cualquier círculo a través del origen debajo del mapa$${\ displaystyle z \ to z ^ {2}}Es un cardioide. Una aplicación de este resultado es que el límite del bulbo central del conjunto de Mandelbrot es un cardioide dado por la ecuación

$${\ displaystyle c \, = \, {\ frac {1- \ left (e ^ {it} -1 \ right) ^ {2}} {4}}. \,}

El conjunto de Mandelbrot contiene un número infinito de copias ligeramente distorsionadas de sí mismo y la bombilla central de cualquiera de estas copias más pequeñas es un cardioide aproximado.

La cáustica que aparece en la superficie de esta taza de café es un cardioide.

Cáusticos [ editar ]

Ciertos cáusticos pueden tomar la forma de cardioides. La catacáustica de un círculo con respecto a un punto de la circunferencia es un cardioide. Además, la catacaústica de un cono con respecto a los rayos paralelos a una línea generadora es una superficie cuya sección transversal es un cardioide. Esto se puede ver, como en la fotografía de la derecha, en una copa cónica parcialmente llena de líquido cuando una luz brilla desde una distancia y en un ángulo igual al ángulo del cono. ^[4] La forma de la curva en la parte inferior de una copa cilíndrica es la mitad de una nefroide , que parece bastante similar.