modo normal de un sistema oscilatorio es la frecuencia a la cual la estructura deformable oscilará al ser perturbada. Los modos normales son también llamados frecuencias naturales o frecuencias resonantes. Para cada estructura existe un conjunto de estas frecuencias que es único.
Es usual utilizar un sistema formado por una masa y un resorte para ilustrar el comportamiento de una estructura deformable. Cuando este tipo de sistema es excitado en una de sus frecuencias naturales, todas las masas se mueven con la misma frecuencia. Las fases de las masas son exactamente las mismas o exactamente las contrarias. El significado práctico puede ser ilustrado mediante un modelo de masa y resorte de un edificio. Si un terremoto excita al sistema con una frecuencia próxima a una de las frecuencias naturales el desplazamiento de un piso (nivel) respecto de otro será máximo. Obviamente, los edificios solo pueden soportar desplazamientos de hasta una cierta magnitud. Ser capaz de representar un edificio y encontrar sus modos normales es una forma fácil de verificar si el diseño del edificio es seguro. El concepto de modos normales también es aplicable en teoría ondulatoria, óptica y mecánica cuántica.
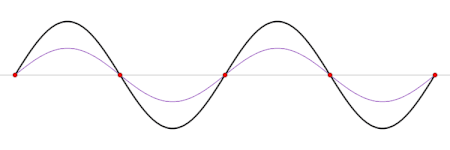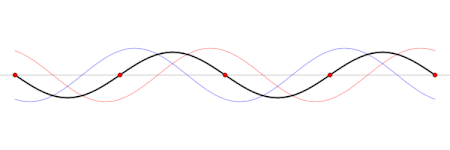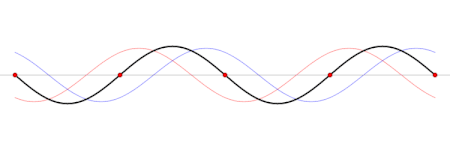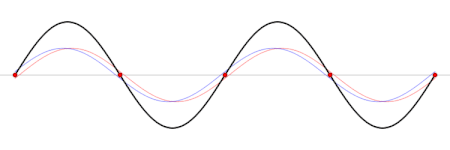
Varios modos normales de una red unidimensional.
Ejemplo - modos normales de osciladores acoplados
Sean dos cuerpos (no afectados por la gravedad), cada uno de ellos de masa M, vinculados a tres resortes con constante característica K. Los mismos se encuentran vinculados de la siguiente manera:
donde los puntos en ambos extremos están fijos y no se pueden desplazar. Se utiliza la variable x1(t) para identificar el desplazamiento de la masa de la izquierda, y x2(t) para identificar el desplazamiento de la masa de la derecha.
Si se indica la derivada segunda de x(t) con respecto al tiempo como x″, las ecuaciones de movimientos son:
Se prueba una solución del tipo:
Sustituyendo estas en las ecuaciones de movimiento se obtiene:
dado que el factor exponencial es común a todos los términos, se puede omitir y simplificar la expresión:
Lo que en notación matricial es:
Para que esta ecuación tenga más solución que la solución trivial, la matriz de la izquierda debe ser singular, por lo tanto el determinante de la matriz debe ser igual a cero, por lo tanto:
Resolviendo para , existen dos soluciones:
- \,
- \,
Si se substituye en la matriz y se resuelve para (), se obtiene (1, 1). Si se substituye , se obtiene (1, -1). (Estos vectores son autovectores (o eigenvectors), y las frecuencias se denominan autovalores, (o eigenvalues).)
El primer modo normal es:
y el segundo modo normal es:
La solución general es una superposición de los modos normales donde c1, c2, φ1, y φ2, son determinados por las condiciones iniciales del problema.
El proceso demostrado aquí puede ser generalizado utilizando el formalismo de la mecánica lagrangiana o el de la mecánica hamiltoniana.
Ondas estacionarias
Una onda estacionaria es una forma continua de modo normal. En una onda estacionaria, todos los elementos del espacio (o sea las coordenadas (x,y,z)) oscilan con la misma frecuencia y en fase (alcanzando el punto de equilibrio juntas), pero cada una de ellas con una amplitud diferente.
La forma general de una onda estacionaria es:
donde f(x, y, z) representan la dependencia de la amplitud con la posición y el seno y coseno son las oscilaciones en el transcurso del tiempo.
En términos físicos, las ondas estacionarias son producidas por la interferencia (superposición) de ondas y sus reflexiones (a pesar de que también es posible decir justamente lo opuesto; que una onda viajera es una superposición de ondas estacionarias). La forma geométrica del medio determina cual será el patrón de interferencia, o sea determina la forma f(x, y, z) de la onda estacionaria. Esta dependencia en el espacio es llamada un modo normal.
Usualmente, en problemas con dependencia continua de (x,y,z) no existe un número determinado de modos normales, en cambio existe un número infinito de modos normales. Si el problema está acotado (o sea está definido en una porción restringida del espacio) existe un número discreto infinito de modos normales (usualmente numerados n = 1,2,3,...). Si el problema no está acotado, existe un espectro continuo de modos normales.
Las frecuencias permitidas dependen de los modos normales como también de las constantes físicas del problema (densidad, tensión, presión, etc.) lo que determina la velocidad de fase de la onda. El rango de todas las frecuencias normales es por lo general llamado el espectro de frecuencias. Por lo general, cada frecuencia está modulada por la amplitud a la cual se ha generado, dando lugar a un gráfico del espectro de potencia de las oscilaciones.
En el ámbito de la música, los modos normales de vibración de los instrumentos (cuerdas, vientos, percusión, etc.) son llamados "armónicos".
Modos normales en mecánica cuántica
En mecánica cuántica, el estado de un sistema se describe por su función de onda , la cual es una solución de la ecuación de Schrödinger. El cuadrado del valor absoluto de , o sea:
Usualmente, cuando se relaciona con algún tipo de potencial, la función de onda se descompone en la superposición de autovectores de energía definida, cada uno oscilando con una frecuencia . Por lo tanto, se puede expresar:
Los autovectores poseen un significado físico más allá de la base ortonormal. Cuando se mide la energía del sistema, la función de onda colapsa en uno de sus autovectores y por lo tanto la función de onda de la partícula se describe por el autovector puro correspondiente a la energía medida.
modos normales de vibración de una cuerda cuyos extremos están fijos por otro procedimiento más general que nos va a servir de modelo para describir los modos de vibración de una barra con ambos extremos fijos.
Ondas estacionarias en una cuerda
- La ecuación diferencial del movimiento ondulatorio es
siendo v la velocidad de propagación de las ondas en la cuerda y ψ el desplazamiento trasversal de un punto x de la cuerda en el instante t.
- Estudiamos una solución de la forma
ψ(x,t)=y(x)·sen(ωt)Cada punto de la cuerda vibra con una amplitud y(x) y con frecuencia angular ω.La ecuación diferencial se convierte enLa solución de esta ecuación diferencial, similar a la de un M.A.S., esy=Asen (kx)+Bcos(kx) con k=ω/v que es el número de onda
- Las condiciones de contorno son:
La cuerda está fija por sus extremos x=0 y x=LDe la primera condición, tenemos que B=0.y de la segunda,sen(kL)=0 o bien, kL=nπ, con n=1, 2, 3,…que nos da los distintas frecuencias de vibración de la cuerda
La amplitud de las oscilaciones de los puntos x de la cuerda en el modo normal n es
Estas funciones cumplen que
La integral es el área bajo la curva de la figura inferior.
Modos normales de vibración de una barra elástica con extremos fijos
Para encontrar los modos normales de vibración de una barra elástica con ambos extremos fijos seguimos un procedimiento similar
- La ecuación diferencial del movimiento de un elemento de la barra es
Siendo ψ el desplazamiento trasversal de un punto x de la barra en el instante t.ρ es la densidad de la barraY es el módulo de Young del material de la barra.I=ab3/12 es el momento de inercia de la sección trasversal rectangular de la barra de anchura a y espesor b.
- Estudiamos una solución de la forma
ψ(x,t)=y(x)·sen(ωt)Cada punto x de la barra vibra con una amplitud y(x) y con frecuencia angular ω.La ecuación diferencial se convierte enLas raíces de la ecuación característica sonson dos raíces reales y dos imaginariasr=q, r=-q, r=iq, r=-iqLa solución general eso de forma equivalentey=A1senh(qx)+A2·cosh(qx)+A3·sen(qx)+A4·cos(qx)La pendiente o derivada de y es,
- Condiciones de contorno.
La barra está firmemente sujeta por sus extremo x=0, y la pendiente en este punto es dy/dx=0.0=A2+A40=A1+A3La barra está firmemente sujeta por sus extremo x=L, y la pendiente en este punto es dy/dx=0.0=A1(senh(qL)-sen(qL))+A2(cosh(qL)-cos(qL))
0=A1(cosh(qL)-cos (qL))+A2(senh(qL)+sen(qL))Eliminado A1 y A2 obtenemos una ecuación trascendente en qL(senh(qL)-sen(qL))·(senh(qL)+sen(qL))-(cosh(qL)-cos (qL))2=0Las raíces rn=qn·L de esta ecuación se calculan por el procedimiento numérico del punto medio, sus primeros cinco valores son:rn=4.73, 7.85, 11.00, 14.14, 17.27Conocido los valores posibles de qn se calculan las frecuencias de vibración ωn=2πfnDonde fn es la frecuencia del modo normal n de vibración y Cn es un número que corresponde a este modo. Sus primeros valores son:C1=3.56, C2=9.82, C3=19.2, C4=31.8, C5=47.5, etc.El coeficiente Cn es independiente de las características de la barra y el segundo término, bajo la raíz, depende del material y de las dimensiones de la barra.La amplitud de la vibración y(x) de los distintos puntos x de la barra en el modo normal de vibración n es:El valor de la constante de proporcionalidad A es la escala vertical. Para que todos los modos de vibración estén dibujados a la misma escala, se calcula A de modo que
Aproximaciones
Cuando qL es grande exp(-qL)≈0 y el seno y el coseno hiperbólico se pueden aproximar a exp(-qL)/2.
Con esta aproximación la ecuación trascendente
(senh(qL)-sen(qL))·(senh(qL)+sen(qL))-(cosh(qL)-cos (qL))2=0
se reduce a
cos(qL)=1/exp(qL).
Si qL es grande cos(qL)=0, Las raíces de esta ecuación son
qnL=π/2+nπ
Los cinco primeros valores de rn=qnL son
rn=4.71, 7.85, 11.00, 14.14, 17.28.
Son prácticamente los mismos, que los calculados resolviendo la ecuación trascendente por procedimientos numéricos
La amplitud y(x) de los distintos puntos x de la barra en el modo normal de vibración n se puede aproximar a
Se puede calcular el valor aproximado de la integral
Para obtener el integrando, hay que integrar dos veces por partes exp(-qnx)·sen(qnx), y lo mismo, exp(-qnx)·cos (qnx).
Para calcular el valor aproximado de la integral, se ha despreciado los términos exp(-qnL) y exp(-2qnL) y por otra parte, cos(2qnL)=0.
Ejemplo:
Sea una barra de acero densidad ρ=7.8 g/cm3, módulo de Young Y=20.6·1010 N/m2
de dimensiones a=2.54 cm de ancho, b=0.76 mm de espesor y longitud L=20.3 cm.
El momento de inercia de la sección trasversal es
I=ab3/12=9.29·10-13 m4
La frecuencia del modo fundamental de vibración vale
La frecuencia del segundo modo normal de vibración será
f2=9.82·27.36=269 Hz
y así, sucesivamente.
Como se describe en el artículo citado en las referencias, se puede diseñar una experiencia que permita excitar un modo normal de vibración de la barra, medir la frecuencia con un osciloscopio, y calcular el módulo de Young de la barra. Previamente, se miden las dimensiones de la barra (longitud, anchura y espesor) con los instrumentos adecuados y se pesa en una balanza para determinar su densidad (masa/volumen).

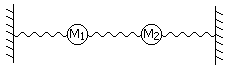










 , existen dos soluciones:
, existen dos soluciones: \,
\, \,
\, en la matriz y se resuelve para (
en la matriz y se resuelve para ( ), se obtiene (1, 1). Si se substituye
), se obtiene (1, 1). Si se substituye  , se obtiene (1, -1). (Estos vectores son
, se obtiene (1, -1). (Estos vectores son 


 de un sistema se describe por su
de un sistema se describe por su  , la cual es una solución de la
, la cual es una solución de la  , o sea:
, o sea:
 . Por lo tanto, se puede expresar:
. Por lo tanto, se puede expresar:
No hay comentarios:
Publicar un comentario