curva con orientación positiva es una curva cerrada simple planar (es decir, una curva en el plano cuyo punto de inicio es también el punto final y que no tiene otras auto-intersecciones) de manera que cuando se viaja en ella, siempre se tiene la curva. Interior a la izquierda (y, en consecuencia, la curva exterior a la derecha). Si en la definición anterior uno se intercambia a la izquierda y a la derecha, se obtiene una curva orientada negativamente .
Crucial para esta definición es el hecho de que cada curva cerrada simple admite un interior bien definido; que se desprende del teorema de la curva de Jordania .
Todas las curvas cerradas simples pueden clasificarse como orientadas negativamente (en el sentido de las agujas del reloj ), orientadas positivamente (en sentido contrario a las agujas del reloj ) o no orientables . El bucle interno de una carretera de circunvalación en los Estados Unidos (u otros países donde las personas conducen en el lado derecho de la carretera) sería un ejemplo de una curva orientada negativamente (en el sentido de las agujas del reloj). Un círculo orientado a la izquierda es un ejemplo de una curva orientada positivamente. El mismo círculo orientado hacia la derecha sería una curva orientada negativamente.
El concepto de orientación de una curva es solo un caso particular de la noción de orientación de una variedad(es decir, además de la orientación de una curva también se puede hablar de orientación de una superficie , hipersuperficie , etc.). Aquí, el interior y el exterior de una curva heredan la orientación habitual del plano. La orientación positiva en la curva es la orientación que hereda como límite de su interior; La orientación negativa se hereda del exterior.
Orientación de un polígono simple [ editar ]
En dos dimensiones, dado un conjunto ordenado de tres o más vértices conectados (puntos) (como en conectar los puntos ) que forma un polígono simple , la orientación del polígono resultante está directamente relacionada con el signo del ángulo en cualquier vérticedel casco convexo del polígono, por ejemplo, del ángulo ABC en la imagen. En los cálculos, el signo del ángulo más pequeño formado por un par de vectores suele estar determinado por el signo del producto cruzado de los vectores. El último se puede calcular como el signo del determinante de su matriz de orientación. En el caso particular cuando los dos vectores están definidos por dossegmentos de línea con punto final común, como los lados BA y BC del ángulo ABC en nuestro ejemplo, la matriz de orientación se puede definir de la siguiente manera:
Se puede obtener una fórmula para su determinante, por ejemplo, utilizando el método de expansión del cofactor:
Si el determinante es negativo, entonces el polígono está orientado hacia la derecha. Si el determinante es positivo, el polígono está orientado en sentido contrario a las agujas del reloj. El determinante es distinto de cero si los puntos A, B y C no son colineales . En el ejemplo anterior, con los puntos ordenados A, B, C, etc., el determinante es negativo y, por lo tanto, el polígono es en sentido horario.
Consideraciones prácticas [ editar ]
En aplicaciones prácticas, las siguientes consideraciones son comúnmente tomadas en cuenta.
Uno no necesita construir el casco convexo de un polígono para encontrar un vértice adecuado. Una opción común es el vértice del polígono con la coordenada X más pequeña. Si hay varios de ellos, se selecciona el que tiene la coordenada Y más pequeña. Se garantiza ser el vértice del casco convexo del polígono. Alternativamente, el vértice con la coordenada Y más pequeña entre las que tienen las coordenadas X más grandes o el vértice con la coordenada X más pequeña entre las que tienen las coordenadas Y más grandes (o cualquiera de las 8 "más pequeñas, las más grandes" X / Y las combinaciones) también lo harán.
Si se busca la orientación de un polígono convexo , entonces, por supuesto, se puede seleccionar cualquier vértice.
Por razones numéricas, la siguiente fórmula equivalente para el determinante se usa comúnmente:
La última fórmula tiene cuatro multiplicaciones menos. Lo que es más importante en los cómputos computacionales involucrados en la mayoría de las aplicaciones prácticas, tales como gráficos de computadora o CAD , los valores absolutos de los multiplicadores son generalmente más pequeños (por ejemplo, cuando A, B, C están dentro del mismo cuadrante ), dando así un valor numérico más pequeño. Error o, en los casos extremos, evitando el desbordamiento aritmético .
Cuando no se sabe de antemano que la secuencia de puntos define un polígono simple, se deben tener en cuenta las siguientes cosas.
Para un polígono de auto-intersección ( polígono complejo ) (o para cualquier curva de auto-intersección) no hay una noción natural del "interior", por lo tanto, la orientación no está definida. Al mismo tiempo, en geometría y gráficos de computadora hay una serie de conceptos para reemplazar la noción de "interior" para curvas cerradas no simples; ver, por ejemplo, " relleno de inundación " y " número de bobinado ".
En los casos "leves" de auto-intersección, con vértices degenerados cuando se permiten tres puntos consecutivos en la misma línea recta y forman un ángulo de cero grados, el concepto de "interior" aún tiene sentido, pero se debe tener un cuidado adicional En la selección del ángulo probado. En el ejemplo dado, imagine que el punto A se encuentra en el segmento BC. En esta situación, el ángulo ABC y su determinante serán 0, por lo tanto inútiles. Una solución es probar esquinas consecutivas a lo largo del polígono (BCD, DEF, ...) hasta que se encuentre un determinante distinto de cero (a menos que todos los puntos se encuentren en la misma línea recta ). (Observe que los puntos C, D, E están en la misma línea y forman un ángulo de 180 grados con cero determinante).
Concavidad local [ editar ]
Una vez que se conoce la orientación de un polígono formado a partir de un conjunto ordenado de vértices, la concavidad de una región local del polígono se puede determinar utilizando una segunda matriz de orientación. Esta matriz se compone de tres vértices consecutivos que se están examinando para determinar la concavidad. Por ejemplo, en el polígono mostrado arriba, si quisiéramos saber si la secuencia de puntos FGH es cóncava , convexa o colineal (plana), construimos la matriz
Si el determinante de esta matriz es 0, entonces la secuencia es colineal, ni cóncava ni convexa. Si el determinante tiene el mismo signo que el de la matriz de orientación para todo el polígono, entonces la secuencia es convexa. Si los signos difieren, entonces la secuencia es cóncava. En este ejemplo, el polígono está orientado negativamente, pero el determinante de los puntos FGH es positivo, por lo que la secuencia FGH es cóncava.
La siguiente tabla ilustra las reglas para determinar si una secuencia de puntos es convexa, cóncava o plana:
| Polígono orientado negativamente (sentido horario) | Polígono orientado positivamente (a la izquierda) | |
|---|---|---|
| El determinante de la matriz de orientación para los puntos locales es negativo. | secuencia convexa de puntos | secuencia cóncava de puntos |
| El determinante de la matriz de orientación para los puntos locales es positivo. | secuencia cóncava de puntos | secuencia convexa de puntos |
| El determinante de la matriz de orientación para los puntos locales es 0. | secuencia colineal de puntos | secuencia colineal de puntos |
En:
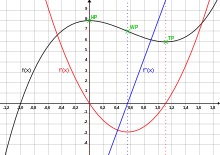
- geometría , curva de dibujo (o curva de rastreo ) incluye técnicas que se pueden utilizar para producir una idea aproximada de la forma general de una curva plana dada su ecuación sin calcular el gran número de puntos requeridos para una parcela detallada. Es una aplicación de la teoría de las curvas para encontrar sus principales características. Aquí la entrada es una ecuación.
- La geometría digital es un método para dibujar una curva píxel por píxel. Aquí la entrada es una matriz (imagen digital)
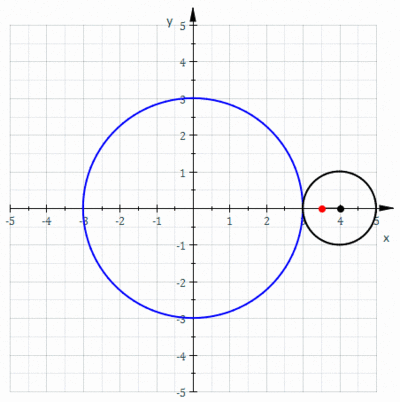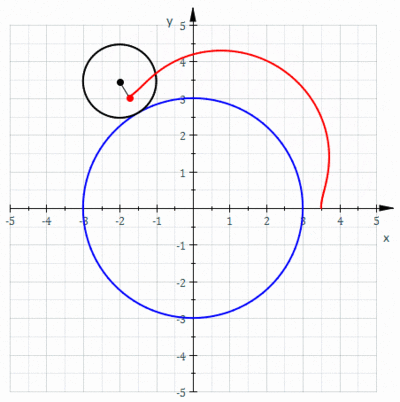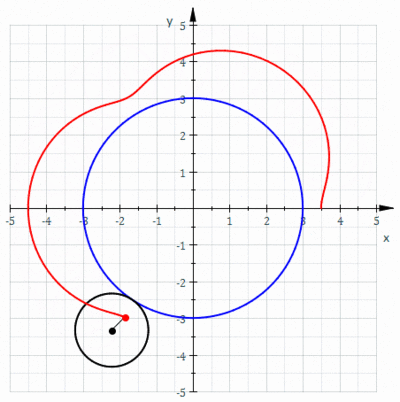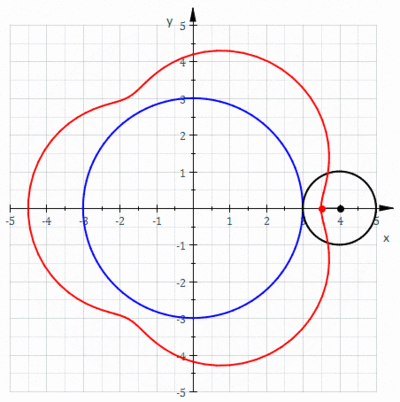
Un ciclocicloide es una ruleta trazada por un punto unido a un círculo de radio r quegira alrededor, un círculo fijo de radio R , donde el punto está a una distancia d del centro del círculo exterior.
dónde Es un parámetro (no el ángulo polar). Y r puede ser positivo o negativo dependiendo de si es de una variedad epicicloide o hipocicloide .
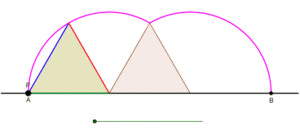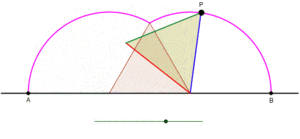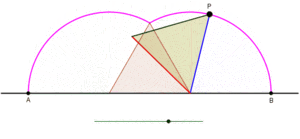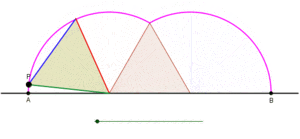
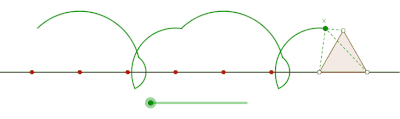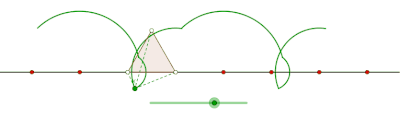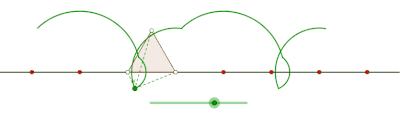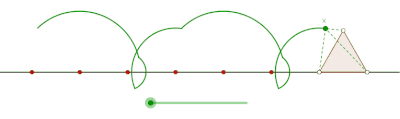
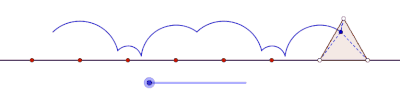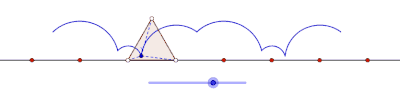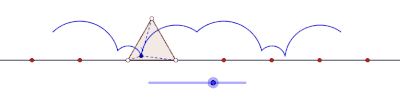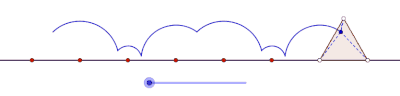
ciclón es la curva trazada por un vértice de un polígono que rueda sin deslizarse a lo largo de una línea recta . [1] [2] No hay restricciones sobre la naturaleza del polígono. Puede ser un polígono regular como un triángulo equilátero o un cuadrado. El polígono ni siquiera debe ser convexo: incluso podría ser un polígono en forma de estrella. Más en general, las curvas trazadas por puntos distintos de los vértices también se han considerado. En tales casos, se supondría que el punto de rastreo está unido rígidamente al polígono. Si el punto de rastreo está ubicado fuera del polígono, entonces la curva se denomina ciclogla prolada, y si se encuentra dentro del polígono se le llama ciclógono curado .
En el límite, a medida que el número de lados aumenta hasta el infinito, el ciclogón se convierte en un cicloide . [3]
El ciclón tiene una propiedad interesante en cuanto a su área. [3] Deje que A denote el área de la región sobre la línea y debajo de uno de los arcos, que P indique el área del polígono rodante, y que C denote el área del disco que circunscribe al polígono. Por cada ciclón generado por un polígono regular,
Ejemplos [ editar ]
Ciclogones generados por un triángulo equilátero y un cuadrado [ editar ]
Prolate ciclogón generado por un triángulo equilátero [ editar ]
Curtate cyclogon generado por un triángulo equilátero [ editar ]
Ciclogones generados por cuadriláteros [ editar ]
Ciclogones generalizados [ editar ]
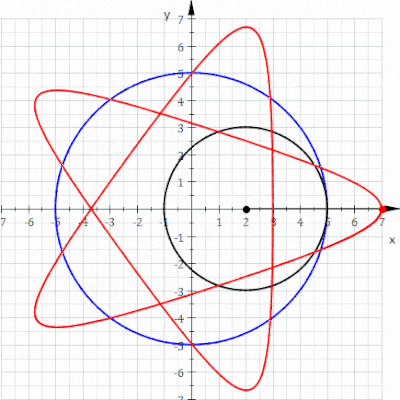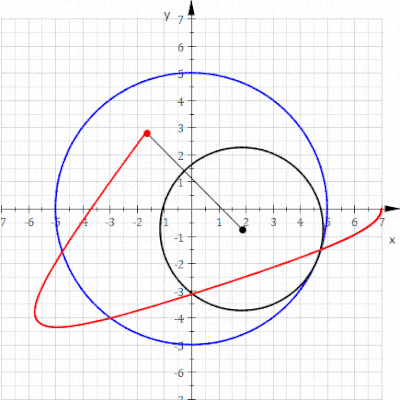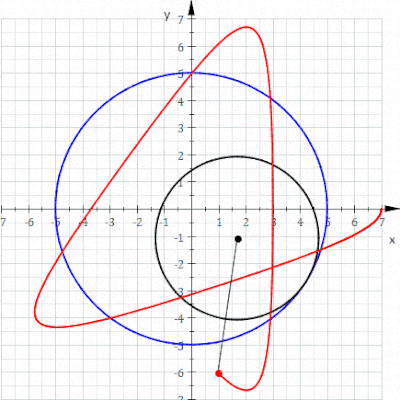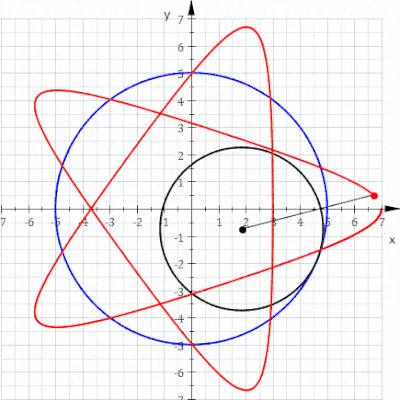
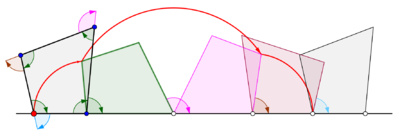
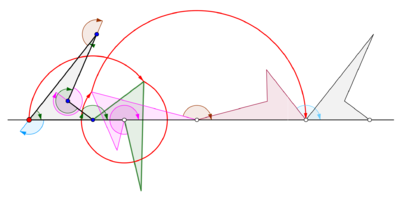
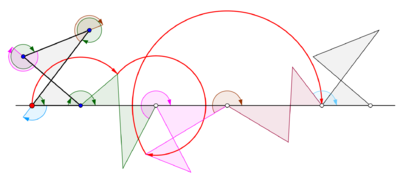
Se obtiene un ciclón cuando un polígono rueda sobre una línea recta. Supongamos que el polígono regular se desplaza sobre el borde de otro polígono. Supongamos también que el punto de rastreo no es un punto en el límite del polígono, sino posiblemente un punto dentro del polígono o fuera del polígono, pero que se encuentra en el plano del polígono. En esta situación más general, deje que una curva sea trazada por un punto z en un disco poligonal regular con n lados que giran alrededor de otro disco poligonal regular con m lados. Se supone que los bordes de los dos polígonos regulares tienen la misma longitud. Un punto z unido rígidamente al n-gon traza un arco que consta de n arcos circulares antes de repetir el patrón periódicamente. Esta curva se llama un trochogon - un epitrochogonsi el n-gon rueda fuera del m-gon, y un hipototroco si rueda dentro del m-gon. El trochogon está curado si z está dentro del n-gon, y prolate (con bucles) si z está fuera del n-gon. Si z está en un vértice, traza un epicicloblo o hipociclo.










No hay comentarios:
Publicar un comentario