GEOMETRÍA ANALÍTICA - CURVAS

geometría afín de las curvas es el estudio de las curvas en un espacio afín , y específicamente las propiedades de dichas curvas que son invariantes bajo el grupo afín especial $${\ displaystyle {\ mbox {SL}} (n, \ mathbb {R}) \ ltimes \ mathbb {R} ^ {n}.}

En la clásica geometría euclidiana de curvas , la herramienta fundamental es el marco Frenet-Serret . En la geometría afín, el marco Frenet-Serret ya no está bien definido, pero es posible definir otro marco canónico en movimiento a lo largo de una curva que juega un papel decisivo similar. La teoría se desarrolló a principios del siglo XX, en gran parte gracias a los esfuerzos de Wilhelm Blaschke y Jean Favard .

El marco afín [ editar ]

Sea x ( t ) una curva en$${\ displaystyle \ mathbb {R} ^ {n}}. Supongamos, como se hace en el caso euclidiano, que las primeras n derivadas de x( t ) son linealmente independientes de modo que, en particular, x ( t ) no se encuentra en ningún subespacio afín de dimensión inferior de$${\ displaystyle \ mathbb {R} ^ {2}}. Entonces el parámetro de la curva t se puede normalizar estableciendo determinante

{\ displaystyle \ det {\ begin {bmatrix} {\ dot {\ mathbf {x}}}, & {\ ddot {\ mathbf {x}}}, & \ dots, & {\ mathbf {x}} ^ { (n)} \ end {bmatrix}} = \ pm 1.}

Se dice que dicha curva está parametrizada por su longitud afín . Para tal parametrización,

$${\ displaystyle t \ mapsto [\ mathbf {x} (t), {\ dot {\ mathbf {x}}} (t), \ dots, \ mathbf {x} ^ {(n)} (t)]}

determina un mapeo en el grupo afín especial, conocido como marco afín especial para la curva. Es decir, en cada punto de las cantidades.$${\ displaystyle \ mathbf {x}, {\ dot {\ mathbf {x}}}, \ dots, \ mathbf {x} ^ {(n)}}Definir un marco afín especial para el espacio afín.$${\ displaystyle \ mathbb {R} ^ {n}}, que consiste en un punto x del espacio y una base lineal especial$${\ displaystyle {\ dot {\ mathbf {x}}}, \ dots, \ mathbf {x} ^ {(n)}}unido al punto en x . El retroceso de la forma de Maurer-Cartan a lo largo de este mapa proporciona un conjunto completo de invariantes estructurales afines de la curva. En el plano, esto da un solo invariante escalar, la curvatura afín de la curva.

Discreta invariante [ editar ]

La normalización del parámetro de la curva s se seleccionó arriba para que

{\ displaystyle \ det {\ begin {bmatrix} {\ dot {\ mathbf {x}}}, & {\ ddot {\ mathbf {x}}}, & \ dots, & {\ mathbf {x}} ^ { (n)} \ end {bmatrix}} = \ pm 1.}

Si n ≡0 (mod 4) o n ≡3 (mod 4), entonces el signo de este determinante es un invariante discreto de la curva. Una curva se llama dextrorse (devanado a la derecha, frecuentemente weinwendig en alemán) si es +1, y sinistrorse (devanado a la izquierda, con frecuencia hopfenwendig en alemán) si es −1.

En tres dimensiones, una hélice diestra es dextrorse, y una hélice zurda es sinistrorse.

Curvatura [ editar ]

Supongamos que la curva x en$${\ displaystyle \ mathbb {R} ^ {n}}Se parametriza por afín arclength. Luego las curvaturas afines , k ₁ ,…, k _n −1de x se definen por

$${\ displaystyle \ mathbf {x} ^ {(n + 1)} = k_ {1} {\ dot {\ mathbf {x}}} + \ cdots + k_ {n-1} \ mathbf {x} ^ {( n-1)}.}

Que tal expresión es posible se sigue calculando la derivada del determinante

{\ displaystyle 0 = \ det {\ begin {bmatrix} {\ dot {\ mathbf {x}}}, & {\ ddot {\ mathbf {x}}}, & \ dots, & {\ mathbf {x}} ^ {(n)} \ end {bmatrix}} {\ dot {}} \, = \ det {\ begin {bmatrix} {\ dot {\ mathbf {x}}}, & {\ ddot {\ mathbf {x }}}, & \ dots, & {\ mathbf {x}} ^ {(n + 1)} \ end {bmatrix}}}

de modo que x ^( n +1) es una combinación lineal de x ′,…, x ^( n −1) .

Considera la matriz

{\ displaystyle A = {\ begin {bmatrix} {\ dot {\ mathbf {x}}}, & {\ ddot {\ mathbf {x}}}, & \ dots, & {\ mathbf {x}} ^ { (n)} \ end {bmatrix}}}

cuyas columnas son las primeras n derivadas de x (aún parametrizadas por arclength afines especiales). Entonces,

{\ displaystyle {\ dot {A}} = {\ begin {bmatrix} 0 & 1 & 0 & 0 & \ cdots & 0 & 0 \\ 0 & 0 & 1 & 0 & \ cdots & 0 & 0 \\\ vdots & \ vdots & \ vdots & \ cdots & \ cdots & \ vdots & \ vdots & \ vdots \ \ 0 & 0 & 0 & 0 & \ cdots & 1 & 0 \\ 0 & 0 & 0 & 0 & \ cdots & 0 & 1 \\ k_ {1} & k_ {2} & k_ {3} & k_ {4} & \ cdots & k_ {n-1} & 0 \ end {bmatrix}} A = CA.}

En términos concretos, la matriz C es el retroceso de la forma Maurer-Cartan del grupo lineal especial a lo largo del marco dado por las primeras n derivadas de x .

curva de plano quártico es una curva algebraica plana de cuarto grado . Se puede definir mediante una ecuación quártica bivariada:

$${\ displaystyle Axe ^ {4} + Por ^ {4} + Cx ^ {3} y + Dx ^ {2} y ^ {2} + Exy ^ {3} + Fx ^ {3} + Gy ^ {3} + Hx ^ {2} y + Ixy ^ {2} + Jx ^ {2} + Ky ^ {2} + Lxy + Mx + Ny + P = 0,}

con al menos uno de A, B, C, D, E no es igual a cero. Esta ecuación tiene 15 constantes. Sin embargo, se puede multiplicar por cualquier constante que no sea cero sin cambiar la curva; por lo tanto, al elegir una constante de multiplicación apropiada, cualquiera de los coeficientes se puede establecer en 1, dejando solo 14 constantes. Por lo tanto, el espacio de las curvas de cuarzo se puede identificar con el espacio proyectivo real $${\ displaystyle \ mathbb {RP} ^ {14}}. También se deduce, según el teorema de Cramer sobre curvas algebraicas , que hay exactamente una curva quártica que pasa a través de un conjunto de 14 puntos distintos en posición general , ya que un quártico tiene 14 grados de libertad .

Una curva quártica puede tener un máximo de:

• Cuatro componentes conectados
• Veintiocho bi-tangentes
• Tres puntos dobles ordinarios .

También se pueden considerar curvas de cuarzo sobre otros campos (o incluso anillos ), por ejemplo, los números complejos . De esta manera, se obtiene superficies de Riemann , que son objetos de una dimensión más de C , pero que son de dos dimensiones sobre R . Un ejemplo es el quártico de Klein . Además, se pueden observar curvas en el plano proyectivo , dadas por polinomios homogéneos.

Ejemplos [ editar ]

Curva comercial

Curva de frijol

Curva bicuspide

Curva de arco

Curva cruciforme con parámetros (b, a) siendo (1,1) en rojo; (2,2) en verde; (3,3) en azul.

Curva cruciforme con parámetros (b, a) siendo (1,1) en rojo; (2,1) en verde; (3,1) en azul.

Seccion espirica

Trébol de tres hojas en coordenadas cartesianas.

Trébol de tres hojas en coordenadas polares.

Varias combinaciones de coeficientes en la ecuación anterior dan lugar a varias familias importantes de curvas como se indica a continuación.

Bicornio Curva de punta de bala Ovalo cartesiano Óvalo de cassini Curva deltoidea Hipopie Kampyle de Eudoxus Klein quartic

Lemniscate Lemniscado de Bernoulli Lemniscado de Gerono Limaçon Lüroth quartic Seccion espirica Squircle La quártica especial de Lamé Seccion torica Curva de trott

Curva Ampersand [ editar ]

La curva de signo es una curva de plano cuártico dada por la ecuación:

$${\ displaystyle \ (y ^ {2} -x ^ {2}) (x-1) (2x-3) = 4 (x ^ {2} + y ^ {2} -2x) ^ {2}.}

Tiene género cero, con tres puntos dobles ordinarios, todos en el plano real. ^[1]

Curva de frijol [ editar ]

La curva de frijol es una curva de plano cuártico con la ecuación:

$${\ displaystyle x ^ {4} + x ^ {2} y ^ {2} + y ^ {4} = x (x ^ {2} + y ^ {2}). \,}

La curva de frijol tiene genero cero. Tiene una singularidad en el origen, un triple punto ordinario. ^[2] [3]

Curva bicúspide [ editar ]

El bicúspide es una curva de plano quártico con la ecuación.

$${\ displaystyle (x ^ {2} -a ^ {2}) (xa) ^ {2} + (y ^ {2} -a ^ {2}) ^ {2} = 0 \,}

donde a determina el tamaño de la curva. El bicúspide tiene solo los dos nodos como singularidades, y por lo tanto es una curva del género uno. ^[4]

Curva de arco [ editar ]

La curva de proa es una curva de plano cuártico con la ecuación:

$${\ displaystyle x ^ {4} = x ^ {2} yy ^ {3}. \,}

La curva de proa tiene un solo punto triple en x = 0, y = 0, y en consecuencia es una curva racional, con el género cero. ^[5]

Curva cruciforme [ editar ]

La curva cruciforme , o curva transversal, es una curva de plano cuártico dada por la ecuación

$${\ displaystyle x ^ {2} y ^ {2} -b ^ {2} x ^ {2} -a ^ {2} y ^ {2} = 0 \,}

donde un y b son dos parámetros que determinan la forma de la curva. La curva cruciforme se relaciona mediante una transformación cuadrática estándar, x ↦ 1 / x , y ↦ 1 / y con la elipse a ² x ² + b ² y ² = 1, y por lo tanto es una curva algebraica de plano racional del género cero. La curva cruciforme tiene tres puntos dobles en el plano proyectivo real , en x = 0 e y = 0, x = 0 y z = 0, y y= 0 y z = 0. ^[6]

Debido a que la curva es racional, puede ser parametrizada por funciones racionales. Por ejemplo, si a = 1 y b = 2, entonces

$${\ displaystyle x = - {\ frac {t ^ {2} -2t + 5} {t ^ {2} -2t-3}}, \ quad y = {\ frac {t ^ {2} -2t + 5 } {2t-2}}}

parametriza los puntos en la curva fuera de los casos excepcionales donde un denominador es cero.

Seccion espirica [ editar ]

Artículo principal: Sección espirica.

Las secciones espiricas se pueden definir como curvas quarticas bicirculares que son simétricas con respecto a los ejes x e y . Las secciones en espiral están incluidas en la familia de secciones tóricas e incluyen la familia de hipopótamos y la familia de óvalos de Cassini . El nombre es de σπειρα que significa toro en griego antiguo.

La ecuación cartesiana se puede escribir como

$${\ displaystyle (x ^ {2} + y ^ {2}) ^ {2} = dx ^ {2} + ey ^ {2} + f,}

y la ecuación en coordenadas polares como

$${\ displaystyle r ^ {4} = dr ^ {2} \ cos ^ {2} \ theta + er ^ {2} \ sin ^ {2} \ theta + f. \,}

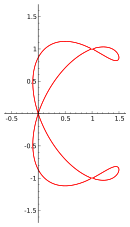
Trébol de tres hojas- [ editar ]

El trébol de tres hojas es la curva del plano quártico.

$${\ displaystyle x ^ {4} + 2x ^ {2} y ^ {2} + y ^ {4} -x ^ {3} + 3xy ^ {2} = 0. \,}

Al resolver para y , la curva se puede describir mediante la siguiente función:

$${\ displaystyle y = \ pm {\ sqrt {\ frac {-2x ^ {2} -3x \ pm {\ sqrt {16x ^ {3} + 9x ^ {2}}}} {2}}},}

donde las dos apariciones de ± son independientes una de la otra, dando hasta cuatro valores distintos de y para cada x .

La ecuación paramétrica del trébol de tres hojas es

$${\ displaystyle x = \ cos (3t) \ cos t, \ quad y = \ cos (3t) \ sin t. \,}^[7]

En coordenadas polares ( x = r  cos φ, y = r  sin) la ecuación es

$${\ displaystyle r = \ cos (3 \ varphi). \,}

Es un caso especial de curva rosa con k = 3. Esta curva tiene un punto triple en el origen (0, 0) y tiene tres tangentes dobles.