GEOMETRÍA ANALÍTICA - CURVAS

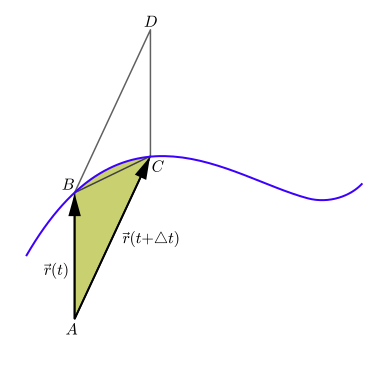
la velocidad de área(también llamada velocidad de sector o velocidad sectorial ) es la velocidad a la que el área es barrida por una partícula a medida que se mueve a lo largo de una curva . En la figura contigua, supongamos que una partícula se mueve a lo largo de la curva azul. En un cierto tiempo t , la partícula se encuentra en el punto B , y un poco más tarde, en el tiempo t Δ + t , la partícula se ha movido al punto C . El área barrida por la partícula es el área verde en la figura, delimitada por los segmentos de línea AB y ACy la curva a lo largo de la cual se mueve la partícula. La velocidad de área es igual a esta área dividida por el intervalo de tiempo Δ t en el límite en que Δ t se vuelve extremadamente pequeño. Es un ejemplo de un pseudovector(también llamado vector axial ), que apunta al plano que contiene los vectores de posición y velocidad de la partícula.

Ilustración de la segunda ley de Kepler. El planeta se mueve más rápido cerca del Sol, por lo que la misma área es barrida en un momento dado como a distancias más grandes, donde el planeta se mueve más lentamente.

El concepto de velocidad de área está estrechamente vinculado históricamente con el concepto de momento angular . La segunda ley de Kepler establece que la velocidad de área de un planeta, con el sol tomado como origen, es constante. Isaac Newton fue el primer científico en reconocer el significado dinámico de la segunda ley de Kepler. Con la ayuda de sus leyes de movimiento, probó en 1684 que cualquier planeta que se siente atraído por un centro fijo arrastra áreas iguales en intervalos de tiempo iguales. A mediados del siglo XVIII, Daniel Bernoulli y Leonhard Euler y Patrick d'Arcydescubrieron gradualmente el principio del momento angular.; La versión de d'Arcy del principio fue expresada en términos de área barrida. Por esta razón, el principio de momento angular se refería a menudo en la literatura más antigua de la mecánica como "el principio de áreas iguales". Dado que el concepto de momento angular incluye más que solo geometría, la designación "principio de áreas iguales" se ha eliminado en las obras modernas.

Conexión con el momento angular [ editar ]

En la situación de la primera figura, el área barrida durante el período de tiempo Δ t por la partícula es aproximadamente igual al área del triángulo ABC . Como Dt tiende a cero esta casi igualdad exacta se convierte como un límite .

Deje que el punto D sea ​​la cuarta esquina del paralelogramo ABDC que se muestra en la figura, de modo que los vectores AB y AC se sumen mediante la regla del paralelogramo al vector AD . Luego, el área del triángulo ABCes la mitad del área del paralelogramo ABDC , y el área de ABDC es igual a la magnitud del producto cruzado de los vectores AB y AC . Esta área también puede verse como un vector con esta magnitud, apuntando en una dirección perpendicular al paralelogramo; este vector es el producto cruzado en sí mismo:

$${\ displaystyle {\ text {área vectorial de paralelogramo}} ABCD = {\ vec {r}} (t) \ times {\ vec {r}} (t + \ Delta t).}

Por lo tanto

$${\ displaystyle {\ text {área vectorial del triángulo}} ABC = {\ frac {{\ vec {r}} (t) \ times {\ vec {r}} (t + \ Delta t)} {2}}. }

La velocidad de área es este área de vector dividida por Δ t en el límite en que Δ t se vuelve muy pequeña:

{\ displaystyle {\ begin {alineado} {\ text {velocidad del área}} & = \ lim _ {\ Delta t \ rightarrow 0} {\ frac {{\ vec {r}} (t) \ times {\ vec { r}} (t + \ Delta t)} {2 \ Delta t}} \\ & = \ lim _ {\ Delta t \ rightarrow 0} {\ frac {{\ vec {r}} (t) \ times {\ bigl (} {\ vec {r}} (t) + {\ vec {r}} \, '(t) \ Delta t {\ bigr)}} {2 \ Delta t}} \\ & = \ lim _ {\ Delta t \ rightarrow 0} {\ frac {{\ vec {r}} (t) \ times {\ vec {r}} \, '(t)} {2}} \ left ({\ Delta t \ sobre \ Delta t} \ derecha) \\ & = {\ frac {{\ vec {r}} (t) \ times {\ vec {r}} \, '(t)} {2}}. \ end { alineado}}}

Pero, $${\ displaystyle {\ vec {r}} \, '(t)} es el vector de velocidad $${\ displaystyle {\ vec {v}} (t)} de la partícula en movimiento, para que

$${\ displaystyle {\ frac {d {\ vec {A}}} {dt}} = {\ frac {{\ vec {r}} \ times {\ vec {v}}} {2}}.}

Por otro lado, el momento angular de la partícula es

$${\ displaystyle {\ vec {L}} = {\ vec {r}} \ times m {\ vec {v}},}

y por lo tanto, el momento angular es igual a 2 m por la velocidad del área.

La conservación de la velocidad de área es una propiedad general del movimiento de fuerza central , ^[1] y, dentro del contexto de la mecánica clásica, es equivalente a la conservación del momento angular.

La velocidad de área es el área barrida por unidad de tiempo por una partícula que se mueve a lo largo de una curva (que se muestra en azul).

 curva asintótica es una curva siempre tangente a una dirección asintótica de la superficie (donde existen). A veces se le llama línea asintótica , aunque no es necesario que sea una línea .

Definiciones [ editar ]

Una dirección asintótica es aquella en la que la curvatura normal es cero. Es decir, para un punto en una curva asintótica, tome el plano que lleva tanto la tangente de la curva como la normal de la superficie en ese punto. La curva de intersección del plano y la superficie tendrá una curvatura cero en ese punto. Las direcciones asintóticas solo pueden ocurrir cuando la curvatura gaussiana es negativa (o cero). Habrá dos direcciones asintóticas a través de cada punto con curvatura gaussiana negativa, divididas en dos por las direcciones principales . Si la superficie es mínima , las direcciones asintóticas son ortogonales entre sí.

Nociones relacionadas [ editar ]

La dirección de la dirección asintótica es la misma que las asíntotas de la hipérbola de la indicatriz de Dupin . ^[1]

Una noción relacionada es una línea de curvatura , que es una curva siempre tangente a una dirección principal.

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Este artículo es sobre arcos en geometría euclidiana. Para el uso especializado en geometría proyectiva, vea Arco (geometría proyectiva) . Para otras aplicaciones, vea Arco (desambiguación) .

Un sector circular está sombreado en verde. Su límite curvo de longitud L es un arco circular.

En la geometría euclidiana , un arco (símbolo: ⌒ ) es un segmento cerrado de una curva diferenciable . Un ejemplo común en el plano (una variedad bidimensional ), es un segmento de un círculo llamado arco circular . En el espacio, si el arco es parte de un gran círculo (o gran elipse), se llama un gran arco .

Cada par de puntos distintos en un círculo determina dos arcos. Si los dos puntos no están directamente opuestos entre sí, uno de estos arcos, el arco menor , subtenderá un ángulo en el centro del círculo que es menor que π radianes(180 grados), y el otro arco, el arco mayor , subtenderá un ángulo mayor que π radianes.

Arcos circulares [ editar ]

Longitud de un arco de un círculo [ editar ]

Ver también: longitud de arco § arcos de círculos

La longitud (más precisamente, la longitud del arco ) de un arco de un círculo con radio r y subtendiendo un ángulo θ (medido en radianes) con el centro del círculo, es decir, el ángulo central , es

$${\ displaystyle L = \ theta r.}

Esto es porque

$${\ displaystyle {\ frac {L} {\ mathrm {circumference}}} = {\ frac {\ theta} {2 \ pi}}.}

Substituyendo en la circunferencia

$${\ displaystyle {\ frac {L} {2 \ pi r}} = {\ frac {\ theta} {2 \ pi}},}

y, siendo α el mismo ángulo medido en grados, ya que θ  =  α/180 π , la longitud del arco es igual a

$${\ displaystyle L = {\ frac {\ alpha \ pi r} {180}}.}

Una forma práctica de determinar la longitud de un arco en un círculo es trazar dos líneas desde los puntos finales del arco hasta el centro del círculo, medir el ángulo donde las dos líneas se encuentran con el centro, luego resolver para L multiplicando de manera cruzada la declaración :

Medida del ángulo en grados / 360 ° = L / circunferencia.

Por ejemplo, si la medida del ángulo es de 60 grados y la circunferencia es de 24 pulgadas, entonces

{\ displaystyle {\ begin {alineado} {\ frac {60} {360}} & = {\ frac {L} {24}} \\ 360L & = 1440 \\ L & = 4. \ end {alineado}}}

Esto es así porque la circunferencia de un círculo y los grados de un círculo, de los cuales siempre hay 360, son directamente proporcionales.

La mitad superior de un círculo se puede parametrizar como

$${\ displaystyle y = {\ sqrt {r ^ {2} -x ^ {2}}}.}

Entonces la longitud del arco de $${\ displaystyle x = a} a $${\ displaystyle x = b} es

$${\ displaystyle L = r {\ Big [} \ arcsin \ left ({\ frac {x} {r}} \ right) {\ Big]} _ {a} ^ {b}.}

Área del sector arco [ editar ]

El área del sector formado por un arco y el centro de un círculo (delimitado por el arco y los dos radios dibujados a sus puntos finales) es

$${\ displaystyle A = {\ frac {r ^ {2} \ theta} {2}}.}

El área A tiene la misma proporción a la zona de círculo como el ángulo θ a un círculo completo:

$${\ displaystyle {\ frac {A} {\ pi r ^ {2}}} = {\ frac {\ theta} {2 \ pi}}.}

Podemos cancelar π en ambos lados:

$${\ displaystyle {\ frac {A} {r ^ {2}}} = {\ frac {\ theta} {2}}.}

Al multiplicar ambos lados por r ² , obtenemos el resultado final:

$${\ displaystyle A = {\ frac {1} {2}} r ^ {2} \ theta.}

Usando la conversión descrita anteriormente, encontramos que el área del sector para un ángulo central medido en grados es

$${\ displaystyle A = {\ frac {\ alpha} {360}} \ pi r ^ {2}.}

Área del segmento de arco [ editar ]

El área de la forma delimitada por el arco y la línea recta entre sus dos puntos finales es

$${\ displaystyle {\ frac {1} {2}} r ^ {2} \ left (\ theta - \ sin {\ theta} \ right).}

Para obtener el área del segmento de arco , necesitamos restar el área del triángulo, determinada por el centro del círculo y los dos puntos finales del arco, del área$${\ displaystyle A}. Ver segmento circular para más detalles.

Radio del arco [ editar ]

El producto de los segmentos de línea AP y PB es igual al producto de los segmentos de línea CP y PD. Si el arco tiene un ancho AB y altura CP, entonces el diámetro del círculo$${\ displaystyle CD = {\ frac {AP \ cdot PB} {CP}} + CP}

Usando el teorema de los acordes de intersección (también conocido como potencia de un punto o teorema de la tangente secante) es posible calcular el radio r de un círculo dada la altura H y el ancho W de un arco:

Considere el acorde con los mismos puntos finales que el arco. Su bisectriz perpendicular es otra cuerda, que es un diámetro del círculo. La longitud del primer acorde es W , y se divide por la bisectriz en dos mitades iguales, cada una con la longitud W/2 . La longitud total del diámetro es 2 r , y está dividida en dos partes por el primer acorde. La longitud de una parte es la sagitta del arco, H , y la otra parte es el resto del diámetro, con una longitud de 2 r  -  H . La aplicación del teorema de los acordes de intersección a estos dos acordes produce

$${\ displaystyle H (2r-H) = \ left ({\ frac {W} {2}} \ right) ^ {2},}

De dónde

$${\ displaystyle 2r-H = {\ frac {W ^ {2}} {4H}},}

asi que

$${\ displaystyle r = {\ frac {W ^ {2}} {8H}} + {\ frac {H} {2}}.}