GEOMETRÍA ANALÍTICA - CURVAS

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Una espiral de doble extremo de Euler. La curva continúa convergiendo hacia los puntos marcados, ya que t tiende a infinito positivo o negativo.

Una espiral de Euler es una curva cuya curvatura cambia linealmente con su longitud de curva (la curvatura de una curva circular es igual al recíproco del radio). Espirales de Euler también se les conoce comúnmente como Spiros , clotoides , o Cornu espirales .

Las espirales de Euler tienen aplicaciones para los cálculos de difracción . También se utilizan ampliamente como curvas de transición en ingeniería ferroviaria / ingeniería de carreteras para conectar y realizar la transición de la geometría entre una curva tangente y una circular. Una aplicación similar también se encuentra en los circuitos integrados fotónicos . El principio de variación lineal de la curvatura de la curva de transición entre una tangente y una curva circular define la geometría de la espiral de Euler:

• Su curvatura comienza con cero en la sección recta (la tangente) y aumenta linealmente con su longitud de curva.
• Cuando la espiral de Euler se encuentra con la curva circular, su curvatura se vuelve igual a la de esta última.

Aplicaciones [ editar ]

Curva de transición de pista [ editar ]

Artículo principal: Curva de transición de la pista

Animación que representa la evolución de una espiral de Cornu con el círculo tangencial con el mismo radio de curvatura que en su punta, también conocido como círculo oscilante (haga clic en la miniatura para observar).

Para viajar a lo largo de una trayectoria circular, un objeto debe estar sujeto a una aceleración centrípeta (por ejemplo: la luna gira alrededor de la tierra debido a la gravedad; un automóvil gira sus ruedas delanteras hacia adentro para generar una fuerza centrípeta). Si un vehículo que viaja en una trayectoria recta pasara repentinamente a una trayectoria circular tangencial, requeriría una aceleración centrípeta que cambia repentinamente en el punto tangente de cero al valor requerido; esto sería difícil de lograr (piense en un conductor que mueva instantáneamente el volante desde la línea recta hasta la posición de giro y que el auto lo haga), ejerciendo una presión mecánica en las partes del vehículo y causando mucha incomodidad (causando sacudidas ).

En los ferrocarriles tempranos, esta aplicación instantánea de la fuerza lateral no fue un problema, ya que se emplearon curvas de baja velocidad y de amplio radio (las fuerzas laterales sobre los pasajeros y la inclinación lateral eran pequeñas y tolerables). A medida que aumentaban las velocidades de los vehículos ferroviarios con el paso de los años, se hizo evidente que era necesaria una servidumbre, de modo que la aceleración centrípeta aumenta linealmente con la distancia recorrida. Dada la expresión de la aceleración centrípeta V² / R , la solución obvia es proporcionar una curva de servidumbre cuya curvatura, 1 / R , aumente linealmente con la distancia recorrida. Esta geometría es una espiral de Euler.

Sin darse cuenta de la solución de la geometría de Leonhard Euler , Rankine citó la curva cúbica (una curva polinomial de grado 3), que es una aproximación de la espiral de Euler para pequeños cambios angulares de la misma manera que una parábola es una aproximación de una circular. curva.

Marie Alfred Cornu (y luego algunos ingenieros civiles) también resolvieron el cálculo de la espiral de Euler de forma independiente. Las espirales de Euler ahora se utilizan ampliamente en la ingeniería ferroviaria y de carreteras para proporcionar una transición o una servidumbre entre una curva circular tangente y horizontal.

Óptica [ editar ]

La espiral de Cornu se puede utilizar para describir un patrón de difracción . ^[1]

Óptica integrada [ editar ]

Las curvas con un radio de curvatura que varía continuamente después de la espiral de Euler también se utilizan para reducir las pérdidas en circuitos fotónicos integrados , ya sea en guías de onda monomodo , ^[2] [3] para suavizar el cambio brusco de curvatura y el acoplamiento a los modos de radiación, o en guías de onda multimodo , ^[4] para suprimir el acoplamiento a los modos de orden superior y garantizar un funcionamiento monomodo efectivo. Una aplicación pionera y muy elegante de la espiral de Euler a las guías de ondas se había realizado desde 1957, ^[5] con una guía de ondas de metal hueco.Para microondas. Allí la idea era explotar el hecho de que una guía de onda de metal recta se puede doblar físicamente para tomar una forma de curva gradual similar a una espiral de Euler.

Automovilismo [ editar ]

El autor de los deportes de motor, Adam Brouillard, ha demostrado el uso de la espiral de Euler para optimizar la línea de carrera durante la parte de la curva de la curva de una vuelta. ^[6]

La tipografía y el dibujo vector digital [ editar ]

Raph Levien lanzó Spiro como kit de herramientas para el diseño de curvas, especialmente el diseño de fuentes, en 2007 ^[7] [8] bajo una licencia gratuita. Este conjunto de herramientas se implementó bastante rápido después en la herramienta de diseño de fuentes Fontforge y en el dibujo vectorial digital Inkscape .

Proyección de mapas [ editar ]

Cortar una esfera a lo largo de una espiral con ancho 1 / N y aplanar la forma resultante produce una espiral de Euler cuando N tiende al infinito. ^[9] Si la esfera es el globo , esto produce una proyección de mapa cuya distorsión tiende a cero, mientras que N tiende al infinito. ^[10]

Formulación [ editar ]

Símbolos [ editar ]

$${\ displaystyle R}	Radio de curvatura
$${\ displaystyle R_ {c}}	Radio de curva circular al final de la espiral.
$${\ displaystyle \ theta}	Ángulo de la curva desde el principio de la espiral (infinito $${\ displaystyle R}) a un punto particular en la espiral.
	Esto también puede medirse como el ángulo entre la tangente inicial y la tangente en el punto en cuestión.
$${\ displaystyle \ theta _ {s}}	Angulo de curva en espiral completa
$${\ displaystyle L, s}	Longitud medida a lo largo de la curva en espiral desde su posición inicial
$${\ displaystyle L_ {s}, s_ {o}}	Longitud de la curva en espiral

esconderDerivación

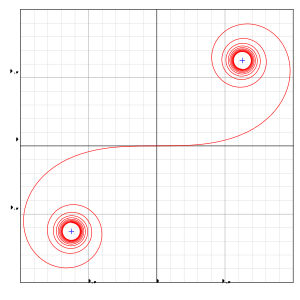
La gráfica de la derecha ilustra una espiral de Euler utilizada como una curva de servidumbre (transición) entre dos curvas dadas, en este caso una línea recta (el eje x negativo ) y un círculo. La espiral comienza en el origen en la dirección x positiva y gira gradualmente en sentido contrario a las agujas del reloj para oscilar el círculo. La espiral es un pequeño segmento de la espiral de Euler de doble extremo anterior en el primer cuadrante. De la definición de la curvatura, $${\ displaystyle {\ frac {1} {R}} = {\ frac {d \ theta} {ds}} \ propto s} es decir $${\ displaystyle Rs = {\ text {constant}} = R_ {c} s_ {o}} $${\ displaystyle {\ frac {d \ theta} {ds}} = {\ frac {s} {R_ {c} s_ {o}}}} Escribimos en el formato, $${\ displaystyle {\ frac {d \ theta} {ds}} = 2a ^ {2} s} Dónde $${\ displaystyle 2a ^ {2} = {\ frac {1} {R_ {c} s_ {o}}}} O $${\ displaystyle a = {\ frac {1} {\ sqrt {2R_ {c} s_ {o}}}}} Así $${\ displaystyle \ theta = (as) ^ {2}} Ahora {\ displaystyle {\ begin {alineado} x & = \ int _ {0} ^ {L} \ cos \ theta \, ds \\ & = \ int _ {0} ^ {L} \ cos \ left [(as) ^ {2} \ right] ds \ end {alineado}}} Si $${\ displaystyle s '= as} Entonces $${\ displaystyle ds = {\ frac {ds '} {a}}} Así $${\ displaystyle x = {\ frac {1} {a}} \ int _ {0} ^ {L '} \ cos {s} ^ {2} ds} {\ displaystyle {\ begin {alineado} y & = \ int _ {0} ^ {L} \ sin \ theta \, ds \\ & = \ int _ {0} ^ {L} \ sin \ left [(as) ^ {2} \ right] ds \\ & = {\ frac {1} {a}} \ int _ {0} ^ {L '} \ sin {s} ^ {2} \, ds \ end {alineado} }}

Expansión de la integral de Fresnel [ editar ]

Artículo principal: Fresnel integral

Si a = 1, que es el caso de la curva de Euler normalizada, entonces las coordenadas cartesianas están dadas por las integrales de Fresnel (o las integrales de Euler):

{\ displaystyle {\ begin {alineado} C (L) & = \ int _ {0} ^ {L} \ cos (s ^ {2}) \, ds \\ S (L) & = \ int _ {0 } ^ {L} \ sin (s ^ {2}) \, ds \ end {alineado}}}

La normalización y la conclusión [ editar ]

Para una curva de Euler dada con:

$${\ displaystyle 2RL = 2R_ {c} L_ {s} = {\ frac {1} {a ^ {2}}}}

o

$${\ displaystyle {\ frac {1} {R}} = {\ frac {L} {R_ {c} L_ {s}}} = 2a ^ {2} L}

entonces

$${\ displaystyle x = {\ frac {1} {a}} \ int _ {0} ^ {L '} \ cos s ^ {2} \, ds}

$${\ displaystyle y = {\ frac {1} {a}} \ int _ {0} ^ {L '} \ sin s ^ {2} \, ds}

dónde $${\ displaystyle L '= aL} y $${\ displaystyle a = {\ frac {1} {\ sqrt {2R_ {c} L_ {s}}}}}.

El proceso de obtención de la solución de ( x , y ) de una espiral de Euler se puede describir así:

• Mapa L de la espiral de Euler original multiplicando con el factor a a L 'de la espiral de Euler normalizada;
• Encuentre ( x ′, y ′) de las integrales de Fresnel; y
• Mapa ( x ′, y ′) a ( x , y ) ampliando (desnormalizar) con factor$${\ displaystyle 1 / a}. Tenga en cuenta que{\ displaystyle 1 / a> 1}.

En el proceso de normalización,

{\ displaystyle {\ begin {alineado} R '_ {c} & = {\ frac {R_ {c}} {\ sqrt {2R_ {c} L_ {s}}}} \\ & = {\ sqrt {\ frac {R_ {c}} {2L_ {s}}}} \\\ end {alineado}}}

{\ displaystyle {\ begin {alineado} L '_ {s} & = {\ frac {L_ {s}} {\ sqrt {2R_ {c} L_ {s}}}} \\ & = {\ sqrt {\ frac {L_ {s}} {2R_ {c}}}} \ end {alineado}}}

Entonces

{\ displaystyle {\ begin {alineado} 2R '_ {c} L' _ {s} & = 2 {\ sqrt {\ frac {R_ {c}} {2L_ {s}}}} {\ sqrt {\ frac {L_ {s}} {2R_ {c}}}} \\ & = {\ tfrac {2} {2}} \\ & = 1 \ end {alineado}}}

Generalmente, la normalización reduce L 'a un valor pequeño (<1 a="" buenas="" caracter="" como="" con="" convergentes="" da="" de="" font="" fresnel="" integral="" la="" manejable="" mayor="" nbsp="" pocos="" precio="" resultado="" rminos="" solo="" sticas="" t="" un="" unos="" y="">inestabilidad numérica del cálculo, especialmente para mayores$${\ displaystyle \ theta} valores.).

Ilustración [ editar ]

Dado:

{\ displaystyle {\ begin {alineado} R_ {c} & = 300 {\ mbox {m}} \\ L_ {s} & = 100 {\ mbox {m}} \ end {alineado}}}

Entonces

{\ displaystyle {\ begin {alineado} \ theta _ {s} & = {\ frac {L_ {s}} {2R_ {c}}} \\ & = {\ frac {100} {2 \ times 300}} \\ & = 0.1667 \ {\ mbox {radian}} \\\ end {alineado}}}

Y

$${\ displaystyle 2R_ {c} L_ {s} = 60,000}

Reducimos la espiral de Euler en √ 60,000 , es decir, 100 √ 6 a la espiral de Euler normalizada que tiene:

$${\ displaystyle {\ begin {alineado} R '_ {c} = {\ tfrac {3} {\ sqrt {6}}} {\ mbox {m}} \\ L' _ {s} = {\ tfrac { 1} {\ sqrt {6}}} {\ mbox {m}} \\\\\ end {alineado}}}

{\ displaystyle {\ begin {alineado} 2R '_ {c} L' _ {s} & = 2 \ times {\ tfrac {3} {\ sqrt {6}}} \ times {\ tfrac {1} {\ sqrt {6}}} \\ & = 1 \ end {alineado}}}

Y

{\ displaystyle {\ begin {alineado} \ theta _ {s} & = {\ frac {L '_ {s}} {2R' _ {c}}} \\ & = {\ frac {\ tfrac {1} {\ sqrt {6}}} {2 \ times {\ tfrac {3} {\ sqrt {6}}}}} \\ & = 0.1667 \ {\ mbox {radian}} \\\ end {alineado}}}

Los dos angulos $${\ displaystyle \ theta _ {s}}son lo mismo. Esto confirma así que las espirales de Euler originales y normalizadas son geométricamente similares. El locus de la curva normalizada se puede determinar a partir de Fresnel Integral, mientras que el locus de la espiral de Euler original se puede obtener al escalar hacia atrás / hacia arriba o desnormalizar.

Otras propiedades de las espirales de Euler normalizadas [ editar ]

Las espirales de Euler normalizadas se pueden expresar como:

$${\ displaystyle x = \ int _ {0} ^ {L} \ cos s ^ {2} ds}

$${\ displaystyle y = \ int _ {0} ^ {L} \ sin s ^ {2} ds}

O expresado como series de potencias :

$${\ displaystyle x = \ left. \ sum _ {i = 0} ^ {\ infty} {\ frac {(-1) ^ {i}} {(2i)!}} {\ frac {s ^ {4i + 1}} {4i + 1}} \ right | _ {0} ^ {L} = \ sum _ {i = 0} ^ {\ infty} {\ frac {(-1) ^ {i}} {(2i )!}} {\ frac {L ^ {4i + 1}} {4i + 1}}}

$${\ displaystyle y = \ left. \ sum _ {i = 0} ^ {\ infty} {\ frac {(-1) ^ {i}} {(2i + 1)!}} {\ frac {s ^ { 4i + 3}} {4i + 3}} \ right | _ {0} ^ {L} = \ sum _ {i = 0} ^ {\ infty} {\ frac {(-1) ^ {i}} { (2i + 1)!}} {\ Frac {L ^ {4i + 3}} {4i + 3}}}

La espiral de Euler normalizada convergerá a un solo punto en el límite, que se puede expresar como:

$${\ displaystyle x ^ {\ prime} = \ lim _ {L \ to \ infty} \ int _ {0} ^ {L} \ cos (s ^ {2}) ds = {\ frac {1} {2} } {\ sqrt {\ frac {\ pi} {2}}}}

$${\ displaystyle y ^ {\ prime} = \ lim _ {L \ to \ infty} \ int _ {0} ^ {L} \ sin (s ^ {2}) ds = {\ frac {1} {2} } {\ sqrt {\ frac {\ pi} {2}}}}

Las espirales de Euler normalizadas tienen las siguientes propiedades:

$${\ displaystyle 2R_ {c} L_ {s} = 1}

$${\ displaystyle \ theta _ {s} = {\ frac {L_ {s}} {2R_ {c}}} = L_ {s} ^ {2}}

Y

$${\ displaystyle \ theta = \ theta _ {s} \ cdot {\ frac {L ^ {2}} {L_ {s} ^ {2}}} = L ^ {2}}

$${\ displaystyle {\ frac {1} {R}} = {\ frac {d \ theta} {dL}} = 2L}

Tenga en cuenta que $${\ displaystyle 2R_ {c} L_ {s} = 1} también significa $${\ displaystyle 1 / R_ {c} = 2L_ {s}}, de acuerdo con la última afirmación matemática.

Código para producir una espiral de Euler [ editar ]

El siguiente código SageMath produce el segundo gráfico anterior. Las primeras cuatro líneas expresan el componente espiral de Euler. Las funciones de Fresnel no se pudieron encontrar. En cambio, se adoptan las integrales de dos series de Taylor expandidas. El código restante expresa respectivamente la tangente y el círculo, incluido el cálculo para las coordenadas del centro.

var ( 'L' ) 
p  =  integral ( taylor ( cos ( L ^ 2 ),  L ,  0 ,  12 ),  L ) 
q  =  integral ( taylor ( sin ( L ^ 2 ),  L ,  0 ,  12 ),  L ) 
r1  =  parametric_plot ([ p ,  q ],  ( L ,  0 , 1 ),  color  =  'rojo' ) 
r2  =  línea ([( - 1.0 ,  0 ),  ( 0 , 0 )],  rgbcolor  =  'azul' ) 
x1  =  p . subs ( L  =  1 ) 
y1  =  q . subs ( L  =  1 ) 
R  =  0.5 
x2  =  x1  -  R * sen ( 1.0 )
y2  =  y1  +  R * cos ( 1.0 ) 
r3  =  círculo (( x2 ,  y2 ),  R ,  rgbcolor  =  'verde' ) 
muestra ( r1  +  r2  +  r3 ,  aspect_ratio  =  1 ,  ejes = falso )

El siguiente es el código de Mathematica para el componente en espiral de Euler (funciona directamente en wolframalpha.com):

Parámetro paramétrico [{
  FresnelC [ Sqrt [ 2 / \ [ Pi ]] t ] / Sqrt [ 2 / \ [ Pi ]], 
  FresnelS [ Sqrt [ 2 / \ [ Pi ]] t ] / Sqrt [ 2 / \ [ Pi ]] 
}, { t , -10 , 10 }]   

El siguiente es el código Xcas para el componente espiral de Euler:

plotparam ([int (cos (u ^ 2), u, 0, t), int (sin (u ^ 2), u, 0, t)], t, -4,4)

El siguiente es el código SageMath para la espiral de Euler de doble extremo completa:

s  =  var ( 's' ) 
parametric_plot (( lambda  s :  numerical_integral ( cos ( x ** 2 ), 0 , s ) [ 0 ],  lambda  s :  numerical_integral ( sin ( x ** 2 ), 0 , s ) [ 0 ]),  ( - 3 * pi / 2 ,  3 * pi / 2))

El siguiente es el código JavaScript para dibujar una espiral de Euler en un elemento de lienzo :

función  drawEulerSpiral ( lienzo ,  T ,  N ,  escala )  { 
      ctx  =  lienzo . getContext ( "2d" ); 
      var  dx ,  dy ,  t = 0 ,  prev  =  { x : 0 ,  y : 0 },  actual ; 
      var  dt  =  T / N ; 
      CTX . beginPath (); 
      mientras que  (N - )  { 
         dx  =  Matemáticas . cos ( t * t )  *  dt ; 
         dy  =  Math . pecado ( t * t )  *  dt ; 
         t  + =  dt ; 
         actual  =  { 
            x :  anterior . x  +  dx , 
            y :  anterior . y  +  dy 
         }; 
         CTX . lineTo ( actual. Escala x * , actual . y * escala ); prev = actual ; } ctx . trazo (); } drawEulerSpiral ( document . getElementById ( "myCanvas" ), 10 , 10000 , 100 ) 
           
      
      

El siguiente es un código de Logo (lenguaje de programación) para dibujar la espiral de Euler utilizando el sprite de tortuga.

rt  90 
repetición  720  [  fd  10  lt  repcount  ]