GEOMETRÍA ANALÍTICA - CURVAS

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

La curva roja es un epicicloide trazado a medida que el círculo pequeño (radio r = 1) gira alrededor del exterior del círculo grande (radio R = 3) .

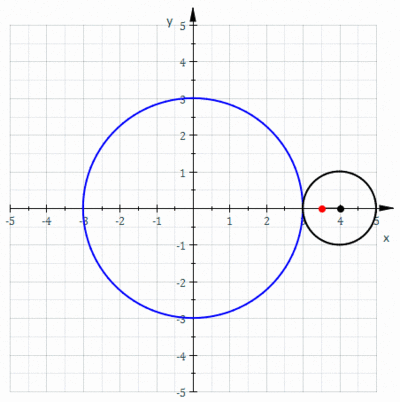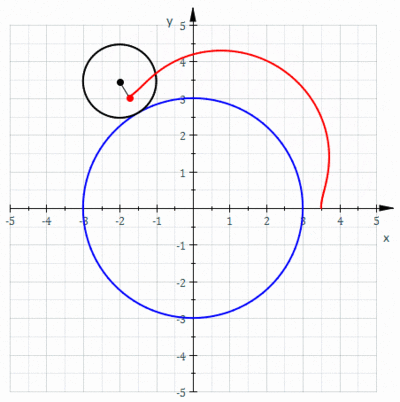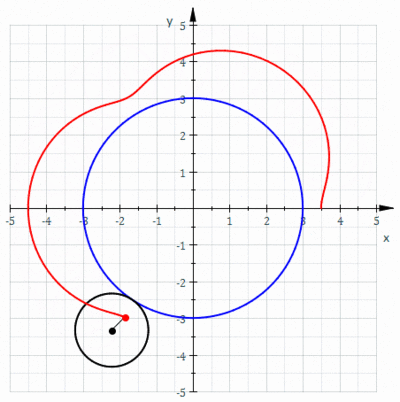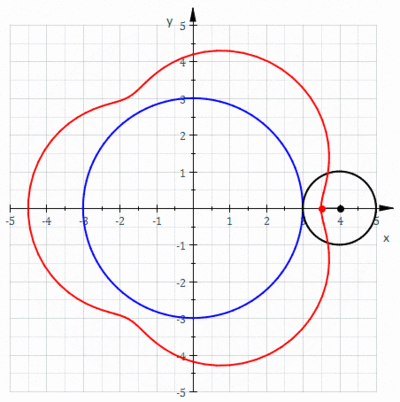
En geometría , un epicicloide o hipercicloide es una curva plana producida al trazar la trayectoria de un punto elegido en la circunferencia de un círculo ( llamado un epiciclo)que rueda sin deslizarse alrededor de un círculo fijo. Es un tipo particular de ruleta .

Ecuaciones [ editar ]

Si el círculo más pequeño tiene un radio r , y el círculo más grande tiene un radio R = kr , entonces lasecuaciones paramétricas de la curva se pueden dar mediante:

$${\ displaystyle x (\ theta) = (R + r) \ cos \ theta \ -r \ cos \ left ({\ frac {R + r} {r}} \ theta \ right)}

$${\ displaystyle y (\ theta) = (R + r) \ sin \ theta \ -r \ sin \ left ({\ frac {R + r} {r}} \ theta \ right),}

o:

$${\ displaystyle x (\ theta) = r (k + 1) \ cos \ theta -r \ cos \ left ((k + 1) \ theta \ right) \,}

$${\ displaystyle y (\ theta) = r (k + 1) \ sin \ theta -r \ sin \ left ((k + 1) \ theta \ right). \,}

(Suponiendo que el punto inicial se encuentra en el círculo más grande.)

Si k es un número entero, entonces la curva está cerrada y tiene k cúspides (es decir, esquinas afiladas, donde la curva no es diferenciable ).

Si k es un número racional , digamos k = p / q expresado en términos más simples, entonces la curva tiene pcusps.

Si k es un número irracional , la curva nunca se cierra y forma un subconjunto denso del espacio entre el círculo más grande y un círculo de radio R + 2 r .

Cuando se mide en radianes, $${\ displaystyle \ theta} toma valor de $${\ displaystyle 0} a $${\ displaystyle 2 * \ pi * {\ frac {LCM (r, R)} {r}}}donde LCM es el mínimo común múltiplo.

• Ejemplos epicicloides
• 

  k = 1
 
• 

  k = 2
 
• 

  k = 3
 
• 

  k = 4
• 

  k = 2.1 = 21/10
 
• 

  k = 3.8 = 19/5
 
• 

  k = 5.5 = 11/2
 
• 

  k = 7.2 = 36/5

El epicicloide es un tipo especial de epitrocoide .

Un epiciclo con una cúspide es un cardioide , dos cúspides es una nefroide .

Un epicicloide y su evolución son similares . ^[1]

Prueba [ editar ]

bosquejo para la prueba

Suponemos que la posición de $${\ displaystyle p} es lo que queremos resolver, $${\ displaystyle \ alpha} es el radio desde el punto tangencial hasta el punto en movimiento $${\ displaystyle p}y $${\ displaystyle \ theta} es el radián desde el punto de partida hasta el punto tangencial.

Como no hay deslizamiento entre los dos ciclos, tenemos que

$${\ displaystyle \ ell _ {R} = \ ell _ {r}}

Por la definición de radián (que es el arco de velocidad sobre el radio), tenemos que

$${\ displaystyle \ ell _ {R} = \ theta R, \ ell _ {r} = \ alpha r}

De estas dos condiciones, obtenemos la identidad.

$${\ displaystyle \ theta R = \ alpha r}

Al calcular, obtenemos la relación entre $${\ displaystyle \ alpha} y $${\ displaystyle \ theta}, cual es

$${\ displaystyle \ alpha = {\ frac {R} {r}} \ theta}

Desde la figura, vemos la posición del punto. $${\ displaystyle p} claramente.

$${\ displaystyle x = \ left (R + r \ right) \ cos \ theta -r \ cos \ left (\ theta + \ alpha \ right) = \ left (R + r \ right) \ cos \ theta -r \ cos \ left ({\ frac {R + r} {r}} \ theta \ right)}

$${\ displaystyle y = \ left (R + r \ right) \ sin \ theta -r \ sin \ left (\ theta + \ alpha \ right) = \ left (R + r \ right) \ sin \ theta -r \ sin \ izquierda ({\ frac {R + r} {r}} \ theta \ derecha)}

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Un epispiral con la ecuación r (θ) = 2sec (2θ)

La epispiral es una curva plana con ecuación polar.

$${\ displaystyle \ r = a \ sec {n \ theta}}.

Hay n secciones si n es impar y 2 n si n es par.

Es la inversión polar o circular de la curva rosa .

En astronomía, epispiral se relaciona con las ecuaciones que explican las órbitas de los planetas .

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

El epitrocoide con R = 3, r = 1 yd = 1/2

Un epitrocoide ( / ɛ p ɪ t r ɒ k ɔɪ d / o / ɛ p ɪ t r oʊ k ɔɪ d / ) es una ruleta trazada por un punto conectado a un círculo de radio r rodando por el exterior de un fijo Círculo de radio R , donde el punto está a una distancia d del centro del círculo exterior.

Las ecuaciones paramétricas para un epitrocoide son

$${\ displaystyle x (\ theta) = (R + r) \ cos \ theta -d \ cos \ left ({R + r \ over r} \ theta \ right), \,}

$${\ displaystyle y (\ theta) = (R + r) \ sin \ theta -d \ sin \ left ({R + r \ over r} \ theta \ right). \,}

dónde $${\ displaystyle \ theta} Es un parámetro (no el ángulo polar).

Los casos especiales incluyen el limaçon con R = r y el epicicloide con d = r .

El clásico juguete Spirograph traza las curvas epitrocoide e hipotrocoide .

Las órbitas de los planetas en el otrora popular sistema ptolemaico geocéntrico son epitrocoides.

La cámara de combustión del motor Wankel es un epitrocoide.

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Curva (rojo) con dos acordes (negro), que se intersecan en el punto equichordal.

En geometría , un punto equichordal es un punto definido en relación con una curva plana convexa de tal manera que todos los acordes quepasan a través del punto son iguales en longitud. Dos figuras comunes con puntos equichordales son el círculo y el limaçon . Es imposible que una curva tenga más de un punto equichordal.

Curvas Equichordal [ editar ]

Una curva se llama equichordal cuando tiene un punto equichordal. ^[1] Dicha curva se puede construir como la curva de pedal de una curva de ancho constante . ^[2] Por ejemplo, la curva del pedal de un círculo es otro círculo (cuando el centro del círculo es el punto del pedal) o una limaçon ; Ambos son curvas equichordales.

Múltiples puntos equichordales [ editar ]

Artículo principal: problema de punto equichordal

En 1916, Fujiwara propuso la pregunta de si una curva podría tener dos puntos equichordales (ofreciendo en el mismo documento una prueba de que tres o más son imposibles). Independientemente, un año después, Blaschke, Rothe y Weitzenböck plantearon la misma pregunta. ^[3] El problema siguió sin resolverse hasta que finalmente fue probado como imposible en 1996 por Marek Rychlik . ^[4] [5] A pesar de su formulación elemental, el problema del punto equichordal era difícil de resolver. El teorema de Rychlik está probado por métodos de análisis complejo avanzado y geometría algebraica y tiene 72 páginas.