GEOMETRÍA ANALÍTICA - CURVAS

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

La evolución de una curva(parábola azul) es el lugar de todos sus centros de curvatura (rojo).

La evolución de una curva (en este caso, una elipse) es la envoltura de sus normales.

En la geometría diferencial de las curvas , la evolución de una curva es el lugar de todos sus centros de curvatura . Es decir, cuando se dibuja el centro de curvatura de cada punto de una curva, la forma resultante será la evolución de esa curva. La evolución de un círculo es, por lo tanto, un único punto en su centro. ^[1] Equivalentemente, una evolución es la envoltura de las normales a una curva.

La evoluta de una curva, una superficie, o más generalmente una subvariedad , es la cáustica del mapa normal. Sea M una sub- estructura suave y regular en ℝ ⁿ . Para cada punto p en M y cada vector v , basado en p y normal a M , asociamos el punto p + v . Esto define un mapa lagrangiano , llamado mapa normal. La cáustica del mapa normal es la evoluta de M . ^[2]

Evolutas están estrechamente conectados a involuciona : Una curva es la evoluta de cualquiera de sus involuciona.

Historia [ editar ]

Apolonio ( c. 200 aC) discutió las evoluciones en el Libro V de sus Cónicas . Sin embargo, a Huygens a veces se le atribuye ser el primero en estudiarlos (1673). Huygens formuló su teoría de la evolución en algún momento alrededor de 1659 para ayudar a resolver el problema de encontrar la curva de tautocrona , que a su vez lo ayudó a construir un péndulo isócrono. Esto se debió a que la curva de tautocrona es un cicloide , y el cicloide tiene la propiedad única de que su evolución es también un cicloide. La teoría de los evolutos, de hecho, le permitió a Huygens lograr muchos resultados que luego se encontrarían usando el cálculo. ^[3]

Evolute de una curva paramétrica [ editar ]

Si $${\ displaystyle {\ vec {x}} = {\ vec {c}} (t), \; t \ en [t_ {1}, t_ {2}]}es la representación paramétrica de una curva regular en el plano con su curvatura en ninguna parte 0 y$${\ displaystyle \ rho (t)} su radio de curvatura y $${\ displaystyle {\ vec {n}} (t)} la unidad normal apunta al centro de curvatura, luego

• $${\ displaystyle {\ vec {E}} (t) = {\ vec {c}} (t) + \ rho (t) {\ vec {n}} (t)}

Describe la evolución de la curva dada.

por $${\ displaystyle {\ vec {c}} (t) = (x (t), y (t)) ^ {T}} y $${\ displaystyle {\ vec {E}} = (X, Y) ^ {T}} uno obtiene

• $${\ displaystyle \ displaystyle X (t) = x (t) - {\ frac {y '(t) \ cdot {\ Big (} x' (t) ^ {2} + y '(t) ^ {2} {\ Big)}} {x '(t) \ cdot y' '(t) -x' '(t) \ cdot y' (t)}} \ quad} y

$${\ displaystyle \ displaystyle Y (t) = y (t) + {\ frac {x '(t) \ cdot {\ Big (} x' (t) ^ {2} + y '(t) ^ {2} {\ Big)}} {x '(t) \ cdot y' '(t) -x' '(t) \ cdot y' (t)}}}.

Propiedades de la evolución [ editar ]

La normal en el punto P es la tangente en el centro de curvatura C.

Para obtener las propiedades de una curva regular es ventajoso utilizar la longitud del arco $${\ displaystyle s} de la curva dada como su parámetro, debido a $${\ displaystyle \; | {\ vec {c}} '| = 1 \;} y $${\ displaystyle \; {\ vec {n}} '= - {\ vec {c}}' / \ rho \;}(ver fórmulas de Frenet – Serret ). De ahí el vector tangente de la evolución.$${\ displaystyle \; {\ vec {E}} = {\ vec {c}} + \ rho {\ vec {n}} \;} es:

$${\ displaystyle {\ vec {E}} '= {\ vec {c}}' + \ rho '{\ vec {n}} + \ rho {\ vec {n}}' = \ rho '{\ vec { n}} \.}

De esta ecuación se obtienen las siguientes propiedades de la evolución:

• En puntos con $${\ displaystyle \ rho '= 0}La evolución no es regular . Eso significa: en los puntos con curvatura máxima o mínima, la evolución tiene cúspides (s. Parábola, elipse, nefroide).
• Las normales de la curva dada son tangentes a la evolución. Por lo tanto: la evolución es la envoltura de las normales de la curva dada.
• En tramos de la curva con {\ displaystyle \ rho '> 0} o {\ displaystyle \ rho '<0 font="">La curva es una involuta de su evolución. (En el diagrama: La parábola azul es una involuta de la parábola semicúbica roja, que en realidad es la evolución de la parábola azul.)

Prueba de la última propiedad: 
Let be{\ displaystyle \ rho '> 0}en la sección de consideración. Una involuta de la evolución puede ser descrita como sigue:

$${\ displaystyle {\ vec {C}} _ ​​{0} = {\ vec {E}} - {\ frac {{\ vec {E}} '} {| {\ vec {E}}' |}} \ ; {\ Big (} \ int _ {0} ^ {s} | {\ vec {E}} '(w) | \; \ mathrm {d} w + l_ {0} \; {\ Big)} \ ;,}

dónde $${\ displaystyle l_ {0}}es una extensión de cadena fija (ver Involutar de una curva parametrizada ). 
Con$${\ displaystyle {\ vec {E}} = {\ vec {c}} + \ rho {\ vec {n}} \;, \; {\ vec {E}} '= \ rho' {\ vec {n }}} y {\ displaystyle \ rho '> 0} uno obtiene

$${\ displaystyle {\ vec {C}} _ ​​{0} = {\ vec {c}} + \ rho {\ vec {n}} - {\ vec {n}} \; {\ Big (} \ int _ {0} ^ {s} \ rho '(w) \; \ mathrm {d} w \; + l_ {0} {\ Big)} = {\ vec {c}} + (\ rho (0) -l_ {0}) \; {\ vec {n}} \ ;.}

Eso significa: Para la extensión de cadena. $${\ displaystyle l_ {0} = \ rho (0)} La curva dada se reproduce.

• Las curvas paralelas tienen la misma evolución.

Prueba: una curva paralela con la distancia.$${\ displaystyle d} fuera de la curva dada tiene la representación paramétrica $${\ displaystyle {\ vec {c}} _ {d} = {\ vec {c}} + d {\ vec {n}}} y el radio de curvatura $${\ displaystyle \ rho _ {d} = \ rho -d}(ver curva paralela ). De ahí que la evolución de la curva paralela sea$${\ displaystyle {\ vec {E}} _ {d} = {\ vec {c}} _ {d} + \ rho _ {d} {\ vec {n}} = {\ vec {c}} + d {\ vec {n}} + (\ rho -d) {\ vec {n}} = {\ vec {c}} + \ rho {\ vec {n}} = {\ vec {E}} \ ;. }

Ejemplos [ editar ]

Evoluta de una parábola [ editar ]

Para la parábola con la representación paramétrica. $${\ displaystyle (t, t ^ {2})} uno obtiene de las fórmulas sobre las ecuaciones:

$${\ displaystyle X = \ cdots = -4t ^ {3}}

$${\ displaystyle Y = \ cdots = {\ frac {1} {2}} + 3t ^ {2} \ ;,}

que describe una parábola semicúbica

Evoluta (roja) de una elipse.

Evoluta de una elipse [ editar ]

Para la elipse con la representación paramétrica. $${\ displaystyle (a \ cos t, b \ sin t)}uno obtiene: ^[4]

$${\ displaystyle X = \ cdots = {\ frac {a ^ {2} -b ^ {2}} {a}} \ cos ^ {3} t}

$${\ displaystyle Y = \ cdots = {\ frac {b ^ {2} -a ^ {2}} {b}} \ sin ^ {3} t \ ;.}

Estas son las ecuaciones de un astroide no simétrico . Eliminando parametro$${\ displaystyle t} Conduce a la representación implícita.

• $${\ displaystyle (aX) ^ {\ tfrac {2} {3}} + (bY) ^ {\ tfrac {2} {3}} = (a ^ {2} -b ^ {2}) ^ {\ tfrac {2} {3}} \.}

Cicloide (azul), su círculo oscilante (rojo) y evolutivo (verde).

Evoluta de una cicloide [ editar ]

Para el cicloide con la representación paramétrica.$${\ displaystyle (r (t- \ sin t), r (1- \ cos t))}La evolución será: ^[5]

$${\ displaystyle X = \ cdots = r (t + \ sin t)}

$${\ displaystyle Y = \ cdots = r (\ cos t-1)}

que describe una réplica transpuesta de sí misma.

La evolución de la nefroide grande (azul) es la nefroide pequeña (roja).

Evolutas de algunas curvas [ editar ]

La evolucion

• de una parábola es una parábola semicúbica (ver arriba),
• de una elipse es un astroide no simétrico (ver arriba),
• de una nefroide es una nefroide (la mitad de grande, vea el diagrama),
• de un astroide es un astroide (el doble de grande),
• de un cardioide es un cardioide (un tercio del tamaño),
• de un círculo es su punto medio,
• de un deltoides es un deltoides (tres veces más grande),
• de un cicloide es un cicloide congruente,
• de una espiral logarítmica es la misma espiral logarítmica,
• De una tractrix es una catenaria.

Curva radial [ editar ]

Una curva con una definición similar es la radial de una curva dada. Para cada punto de la curva, tome el vector desde el punto hasta el centro de curvatura y conviértalo de manera que comience en el origen. Luego, el lugar geométrico de los puntos al final de tales vectores se denomina radial de la curva. La ecuación para el radial se obtiene al eliminar los términos x e y de la ecuación de la evolución. Esto produce

$${\ displaystyle (X, Y) = \ left (-y '{\ frac {{x'} ^ {2} + {y '} ^ {2}} {x'y' '- x''y'} } \;, \; x '{\ frac {{x'} ^ {2} + {y '} ^ {2}} {x'y' '- x''y'}} \ right) \ ;. }

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

La curva de peces con el parámetro de escala a = 1

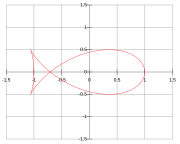
Una curva de pez es una curva de pedal de elipse negativa que tiene la forma de un pez . En una curva de pez, el punto del pedal está en el foco para el caso especial de la excentricidad cuadrada $${\ displaystyle e ^ {2} = {\ tfrac {1} {2}}}. ^[1] Las ecuaciones paramétricaspara una curva de pez corresponden a las de la elipse asociada .

Ecuaciones [ editar ]

Para una elipse con las ecuaciones paramétricas.

$${\ displaystyle \ textstyle {x = a \ cos (t), \ qquad y = {\ frac {a \ sin (t)} {\ sqrt {2}}}},}

La curva de pez correspondiente tiene ecuaciones paramétricas.

$${\ displaystyle \ textstyle {x = a \ cos (t) - {\ frac {a \ sin ^ {2} (t)} {\ sqrt {2}}}, \ qquad y = a \ cos (t) \ pecado (t)}.}

Cuando el origen se traduce al nodo (el punto de cruce), la ecuación cartesiana se puede escribir como: ^[2] [3]

$${\ displaystyle \ left (2x ^ {2} + y ^ {2} \ right) ^ {2} -2 {\ sqrt {2}} ax \ left (2x ^ {2} -3y ^ {2} \ right ) + 2a ^ {2} \ left (y ^ {2} -x ^ {2} \ right) = 0.}

Area [ editar ]

El área de una curva de pez está dada por:

$${\ displaystyle A = {\ frac {1} {2}} \ left | \ int {\ left (xy'-yx '\ right) dt} \ right |}

$${\ displaystyle = {\ frac {1} {8}} a ^ {2} \ left | \ int {\ left [3 \ cos (t) + \ cos (3t) +2 {\ sqrt {2}} \ sin ^ {2} (t) \ right] dt} \ right |},

por lo que el área de la cola y la cabeza están dadas por:

$${\ displaystyle A _ {\ mathrm {Tail}} = \ left ({\ frac {2} {3}} - {\ frac {\ pi} {4 {\ sqrt {2}}}} \ right) a ^ { 2}}

$${\ displaystyle A _ {\ mathrm {Head}} = \ left ({\ frac {2} {3}} + {\ frac {\ pi} {4 {\ sqrt {2}}}} \ right) a ^ { 2}}

Dando el área general para los peces como:

$${\ displaystyle A = {\ frac {4} {3}} a ^ {2}}. ^[2]

Curvatura, longitud de arco y ángulo tangencial [ editar ]

La longitud del arco de la curva está dada por $${\ displaystyle a {\ sqrt {2}} \ left ({\ frac {1} {2}} \ pi +3 \ right)}.

La curvatura de una curva de pez está dada por:

$${\ displaystyle K (t) = {\ frac {2 {\ sqrt {2}} + 3 \ cos (t) - \ cos (3t)} {2a \ left [\ cos ^ {4} t + \ sin ^ { 2} t + \ sin ^ {4} t + {\ sqrt {2}} \ sin (t) \ sin (2t) \ right] ^ {\ frac {3} {2}}}}},

y el ángulo tangencial está dado por: $${\ displaystyle \ phi (t) = \ pi - \ arg \ left ({\ sqrt {2}} - 1 - {\ frac {2} {\ left (1 + {\ sqrt {2}} \ right) e ^ {it} -1}} \ right)}

dónde $${\ displaystyle \ arg (z)} Es el argumento complejo.

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

El folio de Descartes (verde) con asíntota (azul) cuando a = 1.

En geometría , el folio de Descartes es una curva algebraicadefinida por la ecuación.

$${\ displaystyle x ^ {3} + y ^ {3} -3axy = 0 \,}.

Forma un bucle en el primer cuadrante con un punto doble en el origen y una asíntota.

$${\ displaystyle x + y + a = 0 \,}.

Es simetrico acerca de $${\ displaystyle y = x}.

El nombre proviene de la palabra latina folium que significa " hoja ".

La curva se presentó, junto con un retrato de Descartes, en un sello albanés en 1966.

Historia [ editar ]

La curva fue propuesta por primera vez por Descartes en 1638. Su pretensión de fama reside en un incidente en el desarrollo del cálculo . Descartes desafió a Fermat a encontrar la línea tangente a la curva en un punto arbitrario, ya que Fermat había descubierto recientemente un método para encontrar líneas tangentes. Fermat resolvió el problema fácilmente, algo que Descartes no pudo hacer. ^[1] Desde la invención del cálculo, la pendiente de la línea tangente se puede encontrar fácilmente mediante la diferenciación implícita .

Graficando la curva [ editar ]

Dado que la ecuación es el grado 3 tanto en x como en y, y no tiene en cuenta, es difícil de resolver para una de las variables.

Sin embargo, la ecuación en coordenadas polares es:

$${\ displaystyle r = {\ frac {3a \ sin \ theta \ cos \ theta} {\ sin ^ {3} \ theta + \ cos ^ {3} \ theta}}.

que se puede trazar fácilmente. Al usar esta fórmula, se encuentra que el área del interior del bucle es$${\ displaystyle 3a ^ {2} / 2}.

Otra técnica es escribir y = px y resolver para x e y en términos de p. Esto produce las ecuaciones paramétricas racionales : ^[2]

$${\ displaystyle x = {{3ap} \ sobre {1 + p ^ {3}}}, \, y = {{3ap ^ {2}} \ sobre {1 + p ^ {3}}}}.

Podemos ver que el parámetro está relacionado con la posición en la curva de la siguiente manera:

• p <-1 a="" corresponde="" x=""> 0, y <0: ala="" derecha="" font="" inferior="">
• -1 < p <0 a="" corresponde="" x="" y=""> 0: el "ala" superior izquierda.
• p > 0 corresponde a x> 0, y> 0: el bucle de la curva.

Otra forma de trazar la función puede derivarse de la simetría sobre y = x. La simetría se puede ver directamente desde su ecuación (xey pueden intercambiarse). Al aplicar una rotación de 45 ° CW, por ejemplo, se puede trazar la función simétrica sobre el eje x girado.

Esta operación es equivalente a una sustitución:

$${\ displaystyle x = {{u + v} \ sobre {\ sqrt {2}}}, \, y = {{uv} \ sobre {\ sqrt {2}}}}

y rendimientos

$${\ displaystyle v = \ pm u {\ sqrt {\ frac {3a {\ sqrt {2}} - 2u} {6u + 3a {\ sqrt {2}}}}}}

El trazado en el sistema cartesiano de (u, v) proporciona el folio girado en 45 ° y, por lo tanto, simétrico en el eje u.

Dado que el folio es simétrico $${\ displaystyle y = x}, pasa por el punto $${\ displaystyle (3a / 2,3a / 2)}.

Relación con la trisectriz de MacLaurin [ editar ]

El folio de Descartes está relacionado con el trisectrix de Maclaurin por transformación afín . Para ver esto, comienza con la ecuación.

$${\ displaystyle x ^ {3} + y ^ {3} = 3axy \,},

y cambiar variables para encontrar la ecuación en un sistema de coordenadas girado 45 grados. Esto equivale a establecer$${\ displaystyle x = {{X + Y} \ sobre {\ sqrt {2}}}, y = {{XY} \ sobre {\ sqrt {2}}}}. En el$${\ displaystyle X, Y} plano la ecuación es

$${\ displaystyle 2X (X ^ {2} + 3Y ^ {2}) = 3 {\ sqrt {2}} a (X ^ {2} -Y ^ {2})}.

Si estiramos la curva en la $${\ displaystyle Y} dirección por un factor de $${\ displaystyle {\ sqrt {3}}} esto se convierte en

$${\ displaystyle 2X (X ^ {2} + Y ^ {2}) = a {\ sqrt {2}} (3X ^ {2} -Y ^ {2})}

que es la ecuación de la trisectriz de maclaurina.