Un círculo de una esfera es un círculo que se encuentra en una esfera . Dicho círculo puede formarse como la intersección de una esfera y un plano, o de dos esferas. Un círculo en una esfera cuyo plano pasa por el centro de la esfera se llama un gran círculo ; De lo contrario es un pequeño círculo . Los círculos de una esfera tienen un radio menor o igual que el radio de la esfera, con igualdad cuando el círculo es un gran círculo.
En la tierra [ editar ]
En el sistema de coordenadas geográficas de un globo terráqueo, los paralelos de latitud son pequeños círculos, con el Ecuador como único gran círculo. Por el contrario, todos los meridianos de longitud , combinados con su meridiano opuesto en el otro hemisferio , forman grandes círculos.
Terminología relacionada [ editar ]
El diámetro de la esfera que pasa a través del centro del círculo se llama su ejey los puntos finales de este diámetro se llaman sus polos . Un círculo de una esfera también se puede definir como el conjunto de puntos a una distancia angular dada de un polo dado.
Esfera plano intersección [ editar ]
Cuando la intersección de una esfera y un plano no está vacía o en un solo punto, es un círculo. Esto puede verse como sigue:
Vamos S ser una esfera con centro O , P un plano que intersecta S . Dibuje OE perpendicular a P y la reunión Pen E . Sean A y B dos puntos diferentes en la intersección. Luego, AOE y BOE son triángulos rectos con un lado común, OE e hipotenuses AO y BO iguales. Por lo tanto, los lados restantes AE y BE son iguales. Esto prueba que todos los puntos en la intersección están a la misma distancia del puntoE en el plano P , en otras palabras, todos los puntos en la intersección se encuentran en un círculo C con el centro E . [1] Esto demuestra que la intersección de P y S está contenido en C . Tenga en cuenta que OE es el eje del círculo.
Consideremos ahora un punto D del círculo C . Desde C radica en P , también lo hace D . Por otro lado, los triángulos AOE y DOE son triángulos rectos con un lado común, OE y patas EA y ED iguales. Por lo tanto, las hipotenusas AO y DO son iguales, e igual al radio de S , de modo que D se encuentra en S . Esto demuestra que C está contenido en la intersección de P y S .
Como corolario, en una esfera hay exactamente un círculo que se puede dibujar a través de tres puntos dados. [2]
La prueba se puede extender para mostrar que los puntos en un círculo son todos una distancia angular común de uno de sus polos. [3]
Esfera-esfera intersección [ editar ]
Para mostrar que una intersección no trivial de dos esferas es un círculo, asuma (sin pérdida de generalidad) que una esfera (con radio) ) se centra en el origen. Los puntos en esta esfera satisfacen
También sin pérdida de generalidad, supongamos que la segunda esfera, con radio , se centra en un punto en el eje x positivo, a la distancia desde el origen. Sus puntos satisfacen
La intersección de las esferas es el conjunto de puntos que satisfacen ambas ecuaciones. Restar las ecuaciones da
En el caso singular , las esferas son concéntricas. Hay dos posibilidades: si, las esferas coinciden, y la intersección es la esfera entera; Si, las esferas son desunidas y la intersección está vacía. Cuando a no es cero, la intersección se encuentra en un plano vertical con esta coordenada x, que puede intersecar ambas esferas, ser tangente a ambas esferas o externa a ambas esferas. El resultado se sigue de la prueba anterior para las intersecciones esfera-plano.
curva algebraica circular es un tipo de curva algebraica plana determinada por una ecuación F ( x , y ) = 0, donde F es un polinomio con coeficientes reales y los términos de orden más alto de Fforman un polinomio divisible por x 2 + y 2 . Más precisamente, si F = F n + F n −1 + ... + F 1 + F 0 , donde cada F i eshomogénea de grado i , entonces la curva F ( x , y ) = 0 es circular si y solo si F n es divisible por x 2 + y 2 .
De manera equivalente, si la curva se determina en coordenadas homogéneas por G ( x , y , z ) = 0, donde G es un polinomio homogéneo, entonces la curva es circular si y solo si G (1, i , 0) = G (1 , - i , 0) = 0. En otras palabras, la curva es circular si contiene los puntos circulares en el infinito , (1, i , 0) y (1, - i , 0), cuando se considera como una curva en el Plano proyectivo complejo .
Curvas algebraicas Multicircular [ editar ]
Una curva algebraica se llama p -circular si contiene los puntos (1, i , 0) y (1, - i , 0) cuando se considera como una curva en el plano proyectivo complejo, y estos puntos son singularidades de orden al menos p . Los términos bicircular , tricircular , etc. se aplican cuando p = 2, 3, etc. En términos del polinomio F dado anteriormente, la curva F ( x , y ) = 0 es p -circular si F n - i es divisible por ( x 2 + y 2) p - i cuando i < p . Cuando p = 1 esto se reduce a la definición de una curva circular. El conjunto de curvas p -circulares es invariante en las transformaciones euclidianas . Tenga en cuenta que una curva p- circular debe tener un grado de al menos 2 p .
El conjunto de p -circulares de grado p + k , donde p puede variar pero k es un número entero positivo fijo, es invariante bajo inversión . Cuando k es 1, esto dice que el conjunto de líneas (curvas 0-circulares de grado 1) junto con el conjunto de círculos (curvas 1-circulares de grado 2) forman un conjunto que es invariante bajo inversión.
Ejemplos [ editar ]
- El círculo es el único circular cónico.
- Los conchoides de Sluze (que incluyen varias curvas cúbicas conocidas) son cúbicos circulares.
- Los óvalos de Cassini (incluido el lemniscado de Bernoulli ), las secciones tóricas y los limaçons (incluido el cardioide ) son quárticas bicirculares.
- La curva de Watt es una sexticidad tricircular.
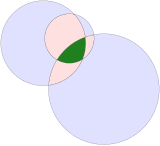 Triángulo circular convexo |  Cuerno triangular circular |
Construcción [ editar ]
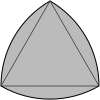 Triangulo reuleaux |  Arbelos |
Un triángulo circular convexo puede construirse mediante tres círculos que se intersecan entre sí y representa el área de intersección. Sus bordes son todos curvados hacia el exterior. La suma de los ángulos internos de un triángulo circular es mayor que 180 °. Un triángulo Reuleaux es un caso especial basado en un triángulo equilátero donde el centro de cada arco está en el vértice opuesto.
Un triángulo de bocina circular es un concepto similar, pero representa el área interior a 3 círculos mutuamente tangentes por lo que todos los ángulos internos son cero. [1]Los arbelos son un caso especial con tres vértices colineales y tres bordes semicirculares . [2]
Otros triángulos circulares pueden tener una mezcla de aristas circulares convexas y cóncavas.
Los arcos largos pueden producir figuras cóncavas, independientemente de si los bordes individuales están curvados hacia dentro o hacia afuera. Los arcos curvados hacia adentro pueden crear formas de auto-intersección, como la figura triquetra :















No hay comentarios:
Publicar un comentario