GEOMETRÍA ANALÍTICA - CURVAS

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Proporciones de células de mamíferos supervivientes a radiación en función de su gravedad (en Gy ). Las líneas negras son radiaciones agudas, mientras que las líneas rojas están fragmentadas temporalmente. Las líneas continuas representan radiación de neutrones y líneas discontinuas de rayos X.

Una curva de supervivencia celular es una curva usada en radiobiología . Representa la relación entre la fracción de células queconservan su integridad reproductiva y la dosis absorbida de radiación. Convencionalmente, la fracción que sobrevive se representa en una escala logarítmica y se representa en el eje y contra la dosis en el eje x.

El modelo cuadrático lineal ahora se usa con más frecuencia para describir la curva de supervivencia celular, asumiendo que existen dos mecanismos para la muerte celular por radiación: un evento letal único o una acumulación de eventos dañinos pero no letales. Las fracciones de supervivencia celular son funciones exponenciales con un término dependiente de la dosis en el exponente debido a las estadísticas de Poisson subyacentes al proceso estocástico. Mientras que los eventos letales únicos conducen a un exponente que está linealmente relacionado con la dosis, la función de fracción de supervivencia para un mecanismo de dos etapas conlleva un exponente proporcional al cuadrado de la dosis. Los coeficientes deben inferirse a partir de los datos medidos, como los datos de la leucemia de Hiroshima. Dado que los órdenes superiores son de menor importancia y la fracción de supervivencia total es el producto de las dos funciones, el modelo se denomina acertadamente lineal-cuadrático.

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Un espejo cóncavo con rayos de luz.

Centro de curvatura

En geometría , el centro de curvatura de una curva se encuentra en un punto que se encuentra a una distancia de la curva igual al radio de curvatura que se encuentra en el vector normal . Es el punto en el infinitosi la curvatura es cero. El círculo oscilante de la curva está centrado en el centro de curvatura. Cauchy definió el centro de curvatura C como el punto de intersección de dos líneas normales infinitamente cercanas a la curva. ^[1] El lugar geométrico de los centros de curvatura para cada punto de la curva comprende la evoluciónde la curva. Este término se utiliza generalmente en Física en relación con el estudio de las lentes.

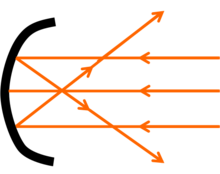
También se puede definir como la distancia esférica entre el punto en el que todos los rayos que caen sobre la lente parecen converger (en el caso de lentes convexas) o divergen de ella (en el caso de las lentes cóncavas) y la lente en sí misma. 

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Un epitrocoide (rojo) con radio de círculo fijo R = 3, radio de círculo rodante r = 1 y distancia d = 1/2 desde el centro del círculo rodante hasta el punto de generación

Un hipotrocoide (rojo) con R = 100, r = 200, d = 100

En geometría , un trocoide centrado es la ruleta formada por un círculo que gira a lo largo de otro círculo. Es decir, es el camino trazado por un punto unido a un círculo cuando el círculo gira sin deslizarse a lo largo de un círculo fijo. El término abarca tanto epitrocoide como hipotrocoide . El centro de esta curva se define como el centro del círculo fijo.

Alternativamente, un trocoide centrado puede definirse como la trayectoria trazada por la suma de dos vectores, cada uno moviéndose a una velocidad uniforme en un círculo. Específicamente, un trocoide centrado es una curva que se puede parametrizar en el plano complejo mediante

$${\ displaystyle z = r_ {1} e ^ {i \ omega _ {1} t} + r_ {2} e ^ {i \ omega _ {2} t}, \,}

o en el plano cartesiano por

$${\ displaystyle x = r_ {1} \ cos (\ omega _ {1} t) + r_ {2} \ cos (\ omega _ {2} t),}

$${\ displaystyle y = r_ {1} \ sin (\ omega _ {1} t) + r_ {2} \ sin (\ omega _ {2} t), \,}

dónde

$${\ displaystyle r_ {1}, r_ {2}, \ omega _ {1}, \ omega _ {2} \ neq 0, \ quad \ omega _ {1} \ neq \ omega _ {2}. \,}

Si $${\ displaystyle \ omega _ {1} / \ omega _ {2}}Es racional entonces la curva es cerrada y algebraica. De lo contrario, la curva se enrolla alrededor del origen un número infinito de veces y es densa en el anillocon el radio exterior.$${\ displaystyle | r_ {1} | + | r_ {2} |} y radio interior $${\ displaystyle || r_ {1} | - | r_ {2} ||}.

Terminología [ editar ]

La mayoría de los autores usan epitrocoide para referirse a una ruleta de un círculo que gira alrededor del exterior de otro círculo, hipototroco significa una ruleta de un círculo que gira alrededor del interior de otro círculo, y trocoide significa una ruleta de un círculo que gira a lo largo de una línea. Sin embargo, algunos autores (por ejemplo, [1] que siguen a F. Morley ) usan "trocoide" para referirse a una ruleta de un círculo que gira a lo largo de otro círculo, aunque esto no es coherente con la terminología más común. El término Trocoide centradoadoptado por [2] combina epitrocoide e hipototrocoide en un solo concepto para racionalizar la exposición matemática y se mantiene consistente con el estándar existente.

El término curva trocoidal describe epitrocoides, hipotrocoides y trocoides (ver [3] ). Una curva trocoidal se puede definir como la trayectoria trazada por la suma de dos vectores, cada uno moviéndose a una velocidad uniforme en un círculo o en una línea recta (pero no ambos moviéndose en una línea).

En las ecuaciones paramétricas dadas anteriormente, la curva es un epitrocoide si $${\ displaystyle \ omega _ {1}} y $${\ displaystyle \ omega _ {2}} tienen el mismo signo, y un hipotrocoide si tienen signos opuestos.

Doble generacion [ editar ]

Deja un círculo de radio. $${\ displaystyle b} ser enrollado en un circulo de radio $${\ displaystyle a}y un punto $${\ displaystyle p}Está unido al círculo rodante. La curva fija se puede parametrizar como$${\ displaystyle f (t) = ae ^ {it}} y la curva de rodadura se puede parametrizar como $${\ displaystyle r (t) = be ^ {i (a / b) t}} o $${\ displaystyle r (t) = - be ^ {- i (a / b) t}}Dependiendo de si la parametrización atraviesa el círculo en la misma dirección o en la dirección opuesta a la parametrización de la curva fija. En cualquier caso podemos usar$${\ displaystyle r (t) = ce ^ {i (a / c) t}} dónde $${\ displaystyle | c | = b}. Dejar$${\ displaystyle p} estar unido al círculo de rodadura en $${\ displaystyle d}. Luego, aplicando la fórmula para la ruleta , el punto traza una curva dada por:

{\ displaystyle {\ begin {alineado} f (t) + (dr (t)) {f '(t) \ over r' (t)} & = ae ^ {it} + (d-ce ^ {i ( a / c) t}) {aie ^ {it} \ over aie ^ {i (a / c) t}} \\ & = (ac) e ^ {it} + de ^ {i (1-a / c ) t}. \ end {alineado}}}

Esta es la parametrización dada anteriormente con $${\ displaystyle r_ {1} = ac}, $${\ displaystyle r_ {2} = d}, $${\ displaystyle \ omega _ {1} = 1}, $${\ displaystyle \ omega _ {2} = 1-a / c}.

A la inversa, dado $${\ displaystyle r_ {1}}, $${\ displaystyle r_ {2}}, $${\ displaystyle \ omega _ {1}}y $${\ displaystyle \ omega _ {2}}, La curva $${\ displaystyle r_ {1} e ^ {i \ omega _ {1} t} + r_ {2} e ^ {i \ omega _ {2} t}} puede ser reparameterizado como $${\ displaystyle r_ {1} e ^ {it} + r_ {2} e ^ {i (\ omega _ {2} / \ omega _ {1}) t}} y las ecuaciones $${\ displaystyle r_ {1} = ac}, $${\ displaystyle r_ {2} = d}, $${\ displaystyle \ omega _ {2} / \ omega _ {1} = 1-a / c} puede ser resuelto para $${\ displaystyle a}, $${\ displaystyle c} y $${\ displaystyle d}Llegar $${\ displaystyle a = r_ {1} (1- \ omega _ {1} / \ omega _ {2}), \ c = -r_ {1} {\ omega _ {1} / \ omega _ {2}} , \ d = r_ {2}.}

La curva $${\ displaystyle r_ {1} e ^ {i \ omega _ {1} t} + r_ {2} e ^ {i \ omega _ {2} t}} permanece igual si los índices 1 y 2 se invierten pero los valores resultantes de $${\ displaystyle a}, $${\ displaystyle c} y $${\ displaystyle d}, en general, no lo hacen. Esto produce el teorema de generación dual que establece que, con la excepción del caso especial que se analiza a continuación, cualquier trocoide centrado se puede generar de dos formas esencialmente diferentes como la ruleta de un círculo que gira sobre otro círculo.

Ejemplos [ editar ]

Cardioide [ editar ]

El cardioide está parametrizado por$${\ displaystyle 2e ^ {it} -e ^ {2it}}. Tomar$${\ displaystyle r_ {1} = 2, r_ {2} = - 1, \ omega _ {1} = 1, \ omega _ {2} = 2} Llegar $${\ displaystyle a = 2 (1-1 / 2) = 1, c = -2 (1/2) = - 1, d = -1}. Ambos círculos tienen un radio de 1 y, dado que c <0 alrededor="" c="" del="" el="" exterior="" fijo.="" font="" gira="" nbsp="" rculo="" rodante="">El punto p es 1 unidad desde el centro de la rodadura, por lo que se encuentra en su circunferencia. Esta es la definición habitual del cardioide. También podemos parametrizar la curva como$${\ displaystyle -e ^ {2it} + 2e ^ {it}}, por lo que también podemos tomar $${\ displaystyle r_ {1} = - 1, r_ {2} = 2, \ omega _ {1} = 2, \ omega _ {2} = 1} Llegar $${\ displaystyle a = -1 (1-2) = 1, b = - (- 1) (2) = 2, d = 2.}En este caso, el círculo fijo tiene un radio 1, el círculo rodante tiene un radio 2 y, dado que c> 0, el círculo giratorio gira alrededor del círculo fijo en la forma de un aro de hula . Esto produce una definición esencialmente diferente de la misma curva.

Elipse [ editar ]

Si $${\ displaystyle \ omega _ {1} = - \ omega _ {2}} entonces obtenemos la curva paramétrica $${\ displaystyle r_ {1} e ^ {it} + r_ {2} e ^ {- it}}o $${\ displaystyle x = (r_ {1} + r_ {2}) \ cos t, y = (r_ {1} -r_ {2}) \ sin t \, \!}. Si$${\ displaystyle | r_ {1} | \ neq | r_ {2} |}, esta es la ecuación de una elipse con ejes.$${\ displaystyle 2 | r_ {1} + r_ {2} |}y $${\ displaystyle 2 | r_ {1} -r_ {2} |}. Evaluando$${\ displaystyle a}, $${\ displaystyle c}y $${\ displaystyle d}como antes; ya sea$${\ displaystyle a = 2r_ {1}, c = r_ {1}, d = r_ {2} \, \!} o $${\ displaystyle a = 2r_ {2}, c = r_ {2}, d = r_ {1} \, \!}. Esto proporciona dos formas diferentes de generar una elipse, ambas implican un círculo que gira dentro de un círculo con el doble del diámetro.

Línea recta [ editar ]

Si además, junto a $${\ displaystyle \ omega _ {1} = - \ omega _ {2}}, $${\ displaystyle r_ {1} = r_ {2} = r}, entonces $${\ displaystyle a = 2r, b = r, c = r \, \!}En ambos casos y las dos formas de generar la curva son las mismas. En este caso la curva es simplemente$${\ displaystyle x = 2r \ cos t, y = 0 \, \!} o un segmento del eje x.

Del mismo modo, si $${\ displaystyle r_ {1} = r, r_ {2} = - r \, \!}, entonces $${\ displaystyle a = 2r, c = r, d = -r \, \!} o $${\ displaystyle a = -2r, c = -r, d = r \, \!}. El círculo es simétrico respecto al origen, por lo que ambos dan el mismo par de círculos. En este caso la curva es simplemente$${\ displaystyle x = 0, y = 2r \ sin t \, \!}: un segmento del eje y.

Entonces el caso $${\ displaystyle \ omega _ {1} = - \ omega _ {2}, \ | r_ {1} | = | r_ {2} |}es una excepción (de hecho, la única excepción) al teorema de generación dual mencionado anteriormente. Este caso degenerado, en el que la curva es un segmento de línea recta, subyace a la pareja Tusi .

 ecuación de Cesàro de una curva plana es una ecuación que relaciona la curvatura ($${\ displaystyle \ kappa}) en un punto de la curva a la longitud del arco ($${\ displaystyle s}) desde el inicio de la curva hasta el punto dado. También se puede dar como una ecuación que relaciona el radio de curvatura ($${\ displaystyle R}) a la longitud del arco . (Estos son equivalentes porque$${\ displaystyle R = 1 / \ kappa}.) Dos curvas congruentes tendrán la misma ecuación de Cesàro. Las ecuaciones de Cesàro llevan el nombre de Ernesto Cesàro .

Ejemplos [ editar ]

Algunas curvas tienen una representación particularmente simple mediante una ecuación de Cesàro. Algunos ejemplos son:

• Línea :$${\ displaystyle \ kappa = 0}.
• círculo :$${\ displaystyle \ kappa = 1 / \ alpha}, dónde $${\ displaystyle \ alpha} es el radio
• Espiral logarítmica :$${\ displaystyle \ kappa = C / s}, dónde $${\ displaystyle C} es una constante
• Círculo involuto :$${\ displaystyle \ kappa = C / {\ sqrt {s}}}, dónde $${\ displaystyle C} es una constante
• Cornu espiral :$${\ displaystyle \ kappa = Cs}, dónde $${\ displaystyle C} es una constante
• catenaria :$${\ displaystyle \ kappa = {\ frac {a} {s ^ {2} + a ^ {2}}}}.

Parametrizaciones relacionadas [ editar ]

La ecuación de Cesàro de una curva está relacionada con su ecuación de Whewell de la siguiente manera. Si la ecuación de Whewell es $${\ displaystyle \ varphi = f (s) \!} entonces la ecuación de Cesàro es $${\ displaystyle \ kappa = f '(s) \!}.