GEOMETRÍA ANALÍTICA - CURVAS

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Tres óvalos de Cassini, que difieren según el rango dentro del cual cae el parámetro e : 0 < e <1 font="" nbsp="" verde="">e = 1 (rojo); 1 < e <$${\ displaystyle {\ sqrt {2}}}(azul). No se muestra: e ≥$${\ displaystyle {\ sqrt {2}}} (convexo).

A Cassini ovalada es un quartic curva plana definida como el conjunto (o locus ) de puntos en el plano de tal manera que el producto de las distancias a dos puntos fijos es constante. Esto puede contrastarse con una elipse , para la cual la suma de las distancias es constante, en lugar del producto. Los óvalos de Cassini son el caso especial de los lemnizados polinomios cuando el polinomio utilizado tiene grado 2.

Los óvalos de Cassini llevan el nombre del astrónomo Giovanni Domenico Cassini quien los estudió en 1680. ^[1]Cassini creía que el Sol viajaba alrededor de la Tierra en uno de estos óvalos, con la Tierra en un foco del óvalo. ^{[ citación necesitada ]} Otros nombres incluyen óvalos de Cassina , curvas y óvalos de Cassini de Cassini .

Definición formal [ editar ]

Óvalo de cassini: $${\ displaystyle | PP_ {1} | \ cdot | PP_ {2} | = b ^ {2}}para cualquier ubicación de P en la curva

• Un óvalo de Cassini es un conjunto de puntos, tal que para cualquier punto$${\ displaystyle P}Del conjunto, el producto de las distancias.$${\ displaystyle | PP_ {1} |, \ | PP_ {2} |} a dos puntos fijos $${\ displaystyle P_ {1}, \; P_ {2}}, es constante, generalmente denotado por {\ displaystyle b ^ {2}, \ b> 0,}:

$${\ displaystyle \ {P \ mid | PP_ {1} | \ cdot | PP_ {2} | = b ^ {2} \} \.}

Al igual que con una elipse, los puntos fijos. $${\ displaystyle P_ {1}, P_ {2}}Se llaman los focos del óvalo de Cassini.

Ecuaciones [ editar ]

Si los focos son ( a , 0) y (- a , 0), entonces la ecuación de la curva es

$${\ displaystyle ((xa) ^ {2} + y ^ {2}) ((x + a) ^ {2} + y ^ {2}) = b ^ {4}. \,}

Cuando se expande esto se convierte en

$${\ displaystyle (x ^ {2} + y ^ {2}) ^ {2} -2a ^ {2} (x ^ {2} -y ^ {2}) + a ^ {4} = b ^ {4 }. \,}

La ecuación polar equivalente es

$${\ displaystyle r ^ {4} -2a ^ {2} r ^ {2} \ cos 2 \ theta = b ^ {4} -a ^ {4}. \,}

Forma [ editar ]

Algunos óvalos de cassini. ( b =  0.6a , 0.8a , a , 1.2a , 1.4a , 1.6a )

La curva depende, hasta la similitud, de e  =  b / a . Cuando e  <1 bucles="" cada="" consta="" contiene="" cuales="" curva="" de="" desconectados="" dos="" foco.="" font="" la="" los="" nbsp="" un="" uno="">Cuando e  = 1, la curva es el lemniscate de Bernoulli que tiene la forma de una figura lateral de ocho con un punto doble (específicamente, un crunode ) en el origen. ^[2] [3] Cuando e  > 1, la curva es un solo bucle conectado que encierra ambos focos. Tiene forma de maní para{\ displaystyle 1  y convexo para $${\ displaystyle e \ geq {\ sqrt {2}}}. ^[4] El caso límite de un → 0 (de ahí e →$${\ displaystyle \ infty}), en cuyo caso los focos coinciden entre sí, es un círculo .

La curva siempre tiene x -interceptos en ± c donde c ²  =  a ²  +  b ² . Cuando e  <1 dos="" font="" hay="" nbsp="">intercepciones x reales adicionales y cuando e  > 1 hay dos intercepciones y reales, todas las demás intercepciones x e y son imaginarias. ^[5]

La curva tiene puntos dobles en los puntos circulares en el infinito , en otras palabras, la curva es bicircular . Estos puntos son biflecnodos, lo que significa que la curva tiene dos tangentes distintas en estos puntos y cada rama de la curva tiene un punto de inflexión allí. De esta información y de las fórmulas de Plücker es posible deducir los números de Plücker para el caso e  ≠ 1: grado = 4, clase = 8, número de nodos = 2, número de cúspides = 0, número de tangentes dobles = 8, número de puntos de inflexión = 12, género = 1. ^[6]

Las tangentes en los puntos circulares están dadas por x  ±  iy  =  ± a que tienen puntos reales de intersección en ( ± a , 0). Así que los focos son, de hecho, focos en el sentido definido por Plücker. ^[7] Los puntos circulares son puntos de inflexión, por lo que son focos triples. Cuando e  ≠ 1, la curva tiene clase ocho, lo que implica que debe haber un total de ocho focos reales. Seis de estos se han contabilizado en los dos focos triples y los dos restantes se encuentran en

{\ displaystyle (\ pm a {\ sqrt {1-e ^ {4}}}, 0) \ quad (e <1 font="">

{\ displaystyle (0, \ pm a {\ sqrt {e ^ {4} -1}}) \ quad (e> 1).}

De modo que los focos adicionales están en el eje x cuando la curva tiene dos bucles y en el eje y cuando la curva tiene un solo bucle. ^[8]

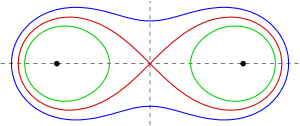
Óvalos de Cassini y trayectorias ortogonales [ editar ]

Óvalos de Cassini y sus trayectorias ortogonales (hiperbolas)

Las trayectorias ortogonales de un lápiz de curvasdadoson curvas que intersectan ortogonalmente a todas las curvas dadas. Por ejemplo, las trayectorias ortogonales de un lápiz de elipses confocales son las hipérbolas confocales con los mismos focos. Para los óvalos de Cassini uno tiene:

• Las trayectorias ortogonales de las curvas de Cassini con focos.$${\ displaystyle P_ {1}, P_ {2}}Son las hiperbolas equiláteras quecontienen$${\ displaystyle P_ {1}, P_ {2}} con el mismo centro que los óvalos de Cassini (ver foto).

Prueba:
por simplicidad se elige$${\ displaystyle P_ {1} = (1,0), \; P_ {2} = (- 1,0)}.

Los óvalos de Cassini tienen la ecuación.

$${\ displaystyle f (x, y) \; = \; (x ^ {2} + y ^ {2}) ^ {2} -2 (x ^ {2} -y ^ {2}) + 1-b ^ {4} = 0.}

Las hiperbolas equiláteras (sus asíntotas son rectangulares) que contienen$${\ displaystyle (1,0), (- 1,0)} con centro $${\ displaystyle (0,0)}puede ser descrito por la ecuación

$${\ displaystyle x ^ {2} -y ^ {2} - \ lambda xy-1 = 0, \ quad \ lambda \ in \ mathbb {R}.}

Estas secciones cónicas no tienen puntos con el eje y en común e intersectan el eje x en $${\ displaystyle (\ pm 1,0)}. Sus discriminantes muestran que estas curvas son hiperbolas. Una investigación más detallada revela que las hipérbolas son rectangulares. Para obtener normales, que son independientes del parámetro.$${\ displaystyle \ lambda} La siguiente representación implícita es más conveniente:

$${\ displaystyle g (x, y) \; = \; {\ frac {x ^ {2} -y ^ {2} -1} {xy}} - \ lambda = {\ frac {x} {y}} - {\ frac {y} {x}} - {\ frac {1} {xy}} - \ lambda = 0 \ ;.}

Un simple cálculo muestra que $${\ displaystyle \ operatorname {grad} f (x, y) \ cdot \ operatorname {grad} g (x, y) = 0} para todos $${\ displaystyle (x, y), \; x \ neq 0 \ neq y}. Por lo tanto, los óvalos de Cassini y las hipérbolas se intersectan ortogonalmente.

Observación:
La imagen que muestra los óvalos de Cassini y los hipérbolas se parece a las curvas equipotenciales de dos cargas de puntos iguales junto con las líneas del campo eléctrico generado. Pero por el potencial de dos cargos de puntos iguales uno tiene$${\ displaystyle {\ frac {1} {| PP_ {1} |}} + {\ frac {1} {| PP_ {2} |}} = {\ text {constant}}}. (Ver curva implícita ).

Ejemplos [ editar ]

El segundo lemniscate del conjunto de Mandelbrot es un óvalo de Cassini definido por la ecuación$${\ displaystyle L_ {2} = \ {c: \ operatorname {abs} (c ^ {2} + c) = ER \} \,}. Sus focos están en los puntos c en el plano complejo que tienen órbitas donde cada segundo valor de z es igual a cero, que son los valores 0 y -1.

Cassini óvalos en tori [ editar ]

Cassini óvalos como secciones planas de un toro 
(el toro de la derecha es un toro de huso )

Los óvalos de Cassini aparecen como secciones planas de toros , pero solo cuando

• El plano de corte es paralelo al eje del toro y su distancia al eje es igual al radio del círculo generador (ver imagen).

La intersección del toro con la ecuación.

$${\ displaystyle \ left (x ^ {2} + y ^ {2} + z ^ {2} + R ^ {2} -r ^ {2} \ right) ^ {2} = 4R ^ {2} \ left (x ^ {2} + y ^ {2} \ derecha)}

y el avion $${\ displaystyle y = r} rendimientos

$${\ displaystyle \ left (x ^ {2} + z ^ {2} + R ^ {2} \ right) ^ {2} = 4R ^ {2} \ left (x ^ {2} + r ^ {2} \Correcto).}

Después de resolver parcialmente el primer corchete se obtiene la ecuación.

$${\ displaystyle \ left (x ^ {2} + z ^ {2} \ right) ^ {2} -2R ^ {2} (x ^ {2} -z ^ {2}) = 4R ^ {2} r ^ {2} -R ^ {4},}

Cuál es la ecuación de un óvalo de Cassini con parámetros $${\ displaystyle b ^ {2} = 2Rr, \; a = R}.

Generalizaciones [ editar ]

El método de Cassini es fácil de generalizar en curvas y superficies con un conjunto arbitrario de puntos de definición:

• $${\ displaystyle | PP_ {1} | \ cdot | PP_ {2} | \ cdots | PP_ {n} | = b ^ {n} \.}

describe en el caso plano una curva implícita y en 3 espacios una superficie implícita .