Una proyección cónica conforme de Lambert ( LCC ) es una proyección de mapa cónico que seutiliza para las cartas aeronáuticas , partes del Sistema de coordenadas del plano estatal y muchos sistemas de mapeo nacionales y regionales. Es una de las siete proyecciones introducidas por Johann Heinrich Lambert en su publicación de 1772 Anmerkungen und Zusätze zur Entwerfung der Land- und Himmelscharten (Notas y comentarios sobre la composición de los mapas terrestres y celestes [1] ).
Conceptualmente, la proyección asienta un conosobre la esfera de la Tierra y proyecta la superficie de manera conforme sobre el cono. El cono se desenrolla y al paralelo que estaba tocando la esfera se le asigna una escala de unidad. Ese paralelo se denomina referencia paralelo o paralelo estándar .
Al escalar el mapa resultante, a dos paralelos se les puede asignar una unidad de escala , disminuyendo la escala entre los dos paralelos y aumentando fuera de ellos. Esto le da al mapa dos paralelos estándar. De esta manera, la desviación de la escala de la unidad se puede minimizar dentro de una región de interés que se encuentra en gran parte entre los dos paralelos estándar. A diferencia de otras proyecciones cónicas, no existe una forma secante verdadera de la proyección porque el uso de un cono secante no produce la misma escala a lo largo de ambos paralelos estándar.
Utilizar [ editar ]
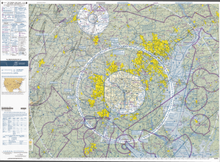
Los pilotos usan cartas aeronáuticas basadas en LCC porque una línea recta dibujada en una proyección cónica conforme de Lambert se aproxima a una ruta de gran círculo entre puntos finales para distancias de vuelo típicas. Los sistemas estadounidenses de VFR ( reglas de vuelo visual ) cartas seccionales y gráficos de áreas terminales están redactados en el LCC con paralelos estándar a 33 ° N y 45 ° N.
La Agencia Europea de Medio Ambiente [3] y la especificación INSPIRE para sistemas de coordenadas [4]recomiendan usar esta proyección (también denominada ETRS89-LCC) para el mapeo paneuropeo conforme a escalas menores o iguales a 1: 500,000. En Francia metropolitana , la proyección oficial es Lambert-93, [5] una proyección cónica de Lambert utilizando el sistema geodésico RGF93 [6] y definida por paralelos de referencia que son 44 ° N y 49 ° N.
El National Spatial Framework para la India utiliza Datum WGS84 con una proyección LCC y es un estándar NNRMS recomendado. Cada estado tiene su propio conjunto de parámetros de referencia dados en el estándar. [7]
El "Sistema de coordenadas del plano estatal de 1983 del Estudio geodésico nacional de los EE. UU. " Utiliza la proyección cónica conforme de Lambert para definir los sistemas de coordenadas de la cuadrícula que se utilizan en varios estados, principalmente aquellos que se alargan de oeste a este, como Tennessee . La proyección de Lambert es relativamente fácil de usar: las conversiones de coordenadas geodésicas ( latitud / longitud ) a cuadrícula del plano estatal incluyen ecuaciones trigonométricas que son bastante sencillas y que se pueden resolver en la mayoría de las calculadoras científicas, especialmente en modelos programables. [8] La proyección como se usa en CCS83 produce mapas en los que los errores de escala se limitan a 1 parte en 10,000.
Historia [ editar ]
La cónica conforme de Lambert es uno de varios sistemas de proyección de mapas desarrollados por Johann Heinrich Lambert , un matemático, físico, filósofo y astrónomo suizo del siglo XVIII. [1]
Transformación [ editar ]
Las coordenadas de un dato esférico se pueden transformar en coordenadas de proyección cónica conforme de Lambert con las siguientes fórmulas, [9] donde λ es la longitud, λ 0 la longitud de referencia, φ la latitud, φ 0 la latitud de referencia, y φ 1 y φ 2 Los paralelos estándar:
![{\ displaystyle {\ begin {alineado} x & = \ rho \ sin \ left [n \ left (\ lambda - \ lambda _ {0} \ right) \ right] \\ y & = \ rho _ {0} - \ rho \ cos \ left [n \ left (\ lambda - \ lambda _ {0} \ right) \ right] \ end {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e30ae340f72c689c692684ce73947881d55fae7)
dónde
![{\ displaystyle {\ begin {alineado} n & = {\ frac {\ ln \ left (\ cos \ varphi _ {1} \ sec \ varphi _ {2} \ right)} {\ ln \ left [\ tan \ left ({\ frac {1} {4}} \ pi + {\ frac {1} {2}} \ varphi _ {2} \ derecha) \ cot \ left ({\ frac {1} {4}} \ pi + {\ frac {1} {2}} \ varphi _ {1} \ right) \ right]}} \\\ rho & = F \ cot ^ {n} \ left ({\ tfrac {1} {4} } \ pi + {\ tfrac {1} {2}} \ varphi \ right) \\\ rho _ {0} & = F \ cot ^ {n} \ left ({\ tfrac {1} {4}} \ pi + {\ tfrac {1} {2}} \ varphi _ {0} \ right) \\ F & = {\ frac {\ cos \ varphi _ {1} \ tan ^ {n} \ left ({\ frac { 1} {4}} \ pi + {\ frac {1} {2}} \ varphi _ {1} \ right)} {n}} \ end {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f82840f5fb60fc811cb0c776786669999352bbaf)
Las fórmulas para datos elipsoidales son más complicadas. [10]
Si se usa un paralelo estándar (es decir, φ 1 = φ 2 ), la fórmula de n anterior es indeterminada, pero luego n = sin ( φ 1 ).
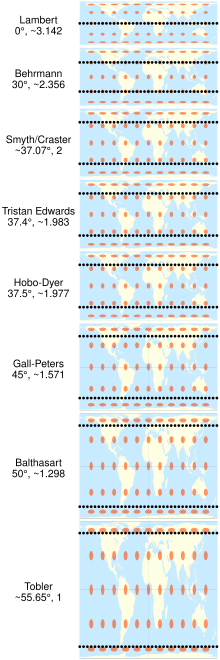
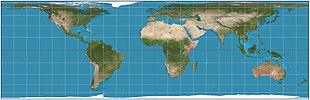
En cartografía , la proyección cilíndrica de igual área de Lambert , o proyección cilíndrica de Lambert , es unaproyección cilíndrica de igual área . Esta proyección no está distorsionada a lo largo del ecuador , que es su paralelo estándar , pero la distorsión aumenta rápidamente hacia los polos. Como cualquier proyección cilíndrica, se estira paralela cada vez más lejos del ecuador. Los polos acumulan una distorsión infinita, convirtiéndose en líneas en lugar de puntos.
Historia [ editar ]
La proyección fue inventada por el matemático suizo Johann Heinrich Lambert y se describe en su tratado de 1772, Beiträge zum Gebrauche der Mathematik und deren Anwendung , parte III, sección 6: Anmerkungen und Zusätze zur Entwerfung der Land- und Himmelscharten , traducido como, Notas y Comentarios Sobre la composición de los mapas terrestres y celestes . [1]
La proyección de Lambert es la base de la familia de proyección cilíndrica de áreas iguales. Lambert eligió el ecuador como el paralelo de no distorsión. [2] Al multiplicar la altura de la proyección por algún factor y al dividir el ancho por el mismo factor, las regiones sin distorsión se pueden mover a cualquier par de paralelos al norte y al sur del ecuador. Estas variaciones, particularmente la proyección de Gall-Peters , se encuentran más comúnmente en los mapas que la proyección original de Lambert debido a su menor distorsión en general. [3]
Fórmulas [ editar ]
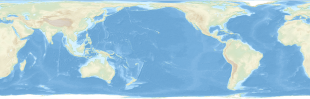
La proyección policónica de latitud igual-diferencial ( 等 差分 纬线 多 多 圆锥 投影 ) es una proyección de mapa policónica en uso desde 1963 en China continental . Los mapas de esta proyección son producidos por la Oficina Estatal de Encuestas y Cartografía de China y otros editores. Su método original de construcción no se ha conservado, pero se ha publicado una aproximación matemática.
Descripción [ editar ]
Como proyección policónica, los paralelos son arcos de círculos que no son concéntricos. Los puntos sin distorsión están en el meridiano central a 44 ° N / S de latitud. Los meridianos son convexos desde el meridiano central recto, y los paralelos son suavemente cóncavos desde el ecuador. La proyección no es ni de área igual ni conforme ; más bien, es una proyección de compromiso.
Los mapas en esta proyección no muestran el polo norte, sino que recortan las latitudes altas a lo largo de una línea recta cuya latitud varía pero que nunca llega al polo. Por convención, la proyección se centra en 150 °, de manera que el Océano Pacífico domina la parte central derecha del mapa y China se ubica a unos 45 ° al oeste del meridiano central, en una ubicación favorable para una baja distorsión. Groenlandia se divide en los bordes izquierdo y derecho del mapa, y el borde norte del mapa recorta las regiones más altas de la isla.
No hay comentarios:
Publicar un comentario