PROYECCIONES DE MAPAS

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Kavrayskiy VII proyección de la tierra .

La proyección de Kavrayskiy VII con la indicativa de deformación de Tissot.

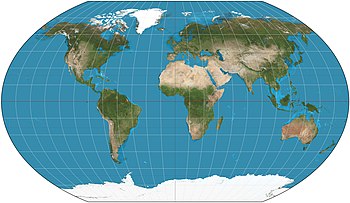
La proyección Kavrayskiy VII es una proyeccióncartográfica inventada por el cartógrafo soviético Vladimir V. Kavrayskiy en 1939 ^[1] para su uso como proyección pseudocilíndrica de propósito general. Al igual que la proyección de Robinson , es un compromiso destinado a producir mapas de buena calidad con una distorsión general baja. En este aspecto, tiene una buena puntuación en comparación con otras proyecciones populares, como Winkel Tripel , ^{[2] [3] a} pesar de los paralelosrectos, espaciados uniformemente y una formulación simple. En cualquier caso, no se ha utilizado ampliamente fuera de la antigua Unión Soviética . ^{[ cita requerida ]}

La proyección se define como:

{\ displaystyle {\ begin {alineado} x & = {\ frac {3 \ lambda} {2}} {\ sqrt {{\ frac {1} {3}} - \ left ({\ frac {\ varphi} {\ pi}} \ derecha) ^ {2}}} \\ y & = \ varphi \ end {alineado}}}

donde λ es la longitud y φ es la latitud en radianes.

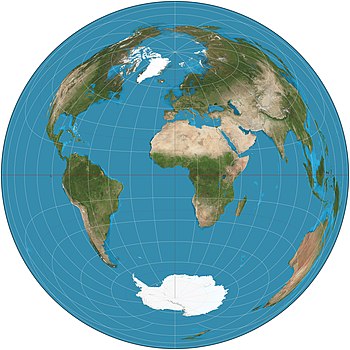
La proyección azimutal de áreas iguales de Lambert es un mapeo particular de una esfera a un disco (es decir, una región delimitada por un círculo). Representa con precisión el área en todas las regiones de la esfera, pero no representa con precisión los ángulos . Se llama así por el matemático suizo Johann Heinrich Lambert , quien lo anunció en 1772. ^[1] "Zenithal" es sinónimo de "azimutal", la proyección también se conoce como proyección zenithal de igual área de Lambert . ^[2]

La proyección azimutal de Lambert se utiliza como proyección cartográfica en cartografía . Por ejemplo, el Atlas Nacional de los EE. UU. Usa una proyección azimutal de áreas iguales de Lambert para mostrar información en la aplicación en línea de Map Maker, ^[3] y la Agencia Europea de Medio Ambiente recomienda su uso para el mapeo europeo para análisis estadísticos y visualización. ^[4]También se utiliza en disciplinas científicas como la geología para trazar las orientaciones de líneas en el espacio tridimensional. Este trazado es asistido por un tipo especial de papel cuadriculado llamado red Schmidt .

Proyección azimutal igual de Lambert del mundo. El centro es 0 ° N 0 ° E. La antípoda es 0 ° N 180 ° E, cerca de Kiribatien el Océano Pacífico . Ese punto está representado por todo el límite circular del mapa, y el océano alrededor de ese punto aparece a lo largo de todo el límite.

Definición [ editar ]

Una sección transversal vista de la esfera y un plano tangente a ella en S . Cada punto de la esfera (excepto la antípoda) se proyecta al plano a lo largo de un arco circular centrado en el punto de tangencia entre la esfera y el plano.

Para definir la proyección azimutal de Lambert, imagine un plano establecido tangente a la esfera en algún punto S en la esfera. Deje que P sea cualquier punto de la esfera que no sea el antípoda de S . Sea d la distancia entre S y P en el espacio tridimensional ( no la distancia a lo largo de la superficie de la esfera). Entonces la proyección envía P a un punto P ' en el plano que está a una distancia d de S .

Para hacer esto más preciso, hay un círculo único centrado en S , que pasa a través de P , y perpendicular al plano. Se cruza el plano en dos puntos; dejó P 'sea el que está más cerca de P . Este es el punto proyectado. Mira la figura. La antípoda de S se excluye de la proyección porque el círculo requerido no es único. El caso de S es degenerado; S se proyecta a sí mismo, a lo largo de un círculo de radio 0. ^[6]

Se requieren fórmulas explícitas para llevar a cabo la proyección en una computadora . Considere la proyección centrada en S = (0, 0, −1) en la esfera unitaria , que es el conjunto de puntos ( x , y , z ) en el espacio tridimensional R ³ tal que x ² + y ² + z ² = 1 . En coordenadas cartesianas ( x , y , z ) en la esfera y ( X , Y) en el plano, la proyección y su inverso se describen a continuación por

{\ displaystyle {\ begin {alineado} (X, Y) & = \ left ({\ sqrt {\ frac {2} {1-z}}} \, x, {\ sqrt {\ frac {2} {1 -z}}} \, y \ right), \\ (x, y, z) & = \ left ({\ sqrt {1 - {\ frac {X ^ {2} + Y ^ {2}} {4 }}}} \, X, {\ sqrt {1 - {\ frac {X ^ {2} + Y ^ {2}} {4}}}} \, Y, -1 + {\ frac {X ^ { 2} + Y ^ {2}} {2}} \ derecha). \ End {alineado}}}

En coordenadas esféricas ( φ , θ ) en la esfera (con φ el cenit y θ el azimut ) y coordenadas polares ( R , Θ ) en el disco, el mapa y su inverso están dados por ^[6]

{\ displaystyle {\ begin {alineado} (R, \ Theta) & = \ left (2 \ cos {\ frac {\ varphi} {2}}, \ theta \ right), \\ (\ varphi, \ theta) & = \ left (2 \ arccos {\ frac {R} {2}}, \ Theta \ right). \ end {alineado}}}

En coordenadas cilíndricas ( r , θ , z ) sobre la esfera y polares coordenadas ( R , Θ ) en el avión, el mapa y su inversa son dados por

{\ displaystyle {\ begin {alineado} (R, \ Theta) & = \ left ({\ sqrt {2 (1 + z)}}, \ theta \ right), \\ (r, \ theta, z) & = \ left (R {\ sqrt {1 - {\ frac {R ^ {2}} {4}}}}, \ Theta, -1 + {\ frac {R ^ {2}} {2}} \ right ). \ end {alineado}}}

La proyección puede centrarse en otros puntos y definirse en esferas de radio distintas de 1, utilizando fórmulas similares. ^[7]

Propiedades [ editar ]

Como se definió en la sección anterior, la proyección azimutal de Lambert de la esfera unitaria no está definida en (0, 0, 1). Envía el resto de la esfera al disco abierto de radio 2 centrado en el origen (0, 0) en el plano. Envía el punto (0, 0, −1) a (0, 0), el ecuador z = 0 al círculo de radio √ 2 centrado en (0, 0) y el hemisferio inferior z <0 abierto="" al="" circulo="" contenido="" disco="" en="" ese="" font="">

La proyección es un difeomorfismo (una bijección que es infinitamente diferenciable en ambas direcciones) entre la esfera (menos (0, 0, 1)) y el disco abierto de radio 2. Es un mapa que preserva áreas (áreas iguales). que se puede ver al calcular el elemento de área de la esfera cuando está parametrizado por la inversa de la proyección. En coordenadas cartesianas es

$${\ displaystyle dA = dX \; dY.}

Esto significa que medir el área de una región en la esfera equivale a medir el área de la región correspondiente en el disco.

Por otro lado, la proyección no conserva las relaciones angulares entre las curvas en la esfera. Ningún mapeo entre una porción de una esfera y el plano puede preservar los ángulos y las áreas. (Si uno lo hiciera, entonces sería una isometría local y preservaría la curvatura gaussiana ; pero la esfera y el disco tienen curvaturas diferentes, por lo que esto es imposible). Este hecho, que las imágenes planas no pueden representar perfectamente regiones de esferas, es el problema fundamental. de la cartografía.

Como consecuencia, las regiones en la esfera pueden proyectarse al plano con formas muy distorsionadas. Esta distorsión es particularmente dramática lejos del centro de la proyección (0, 0, −1). En la práctica, la proyección a menudo está restringida al hemisferio centrado en ese punto; el otro hemisferio se puede mapear por separado, usando una segunda proyección centrada en la antípoda.

Aplicaciones [ editar ]

La proyección azimutal de Lambert se concibió originalmente como una proyección de mapa de áreas iguales. Ahora también se usa en disciplinas como la geología para trazar datos direccionales, de la siguiente manera.

Una dirección en el espacio tridimensional corresponde a una línea a través del origen. El conjunto de todas estas líneas es en sí mismo un espacio, llamado el plano proyectivo real en matemáticas . Cada línea a través del origen intersecta la esfera unitaria en exactamente dos puntos, uno de los cuales está en el hemisferio inferior z ≤ 0. (Las líneas horizontales intersectan el ecuador z = 0 en dos puntos antípodas. Se entiende que los puntos antípodas en el ecuador representan una sola línea. Consulte la topología del cociente .) Por lo tanto, las direcciones en el espacio tridimensional corresponden (casi perfectamente) a los puntos en el hemisferio inferior. El hemisferio se puede representar como un disco de radio √ 2 Utilizando la proyección azimutal de Lambert.

De este modo, la proyección azimutal de Lambert nos permite trazar direcciones como puntos en un disco. Debido a la propiedad de la zona de igual proyección de la proyección, uno puede integrarse sobre regiones del plano proyectivo real (el espacio de direcciones) al integrarse sobre las regiones correspondientes en el disco. Esto es útil para el análisis estadístico de datos direccionales ^[6] , incluida la rotación rígida aleatoria ^[8] .

No solo las líneas, sino también los planos a través del origen se pueden trazar con la proyección azimutal de Lambert. Un plano intersecta el hemisferio en un arco circular, llamado traza del plano, que se proyecta hacia una curva (generalmente no circular) en el disco. Uno puede trazar esta curva, o alternativamente puede reemplazar el plano con la línea perpendicular a ella, llamada el polo , y trazar esa línea en su lugar. Cuando muchos planos se trazan juntos, trazar polos en lugar de trazas produce un trazado menos abarrotado.

Los investigadores en geología estructural utilizan la proyección azimutal Lambert para trazar cristalográficosejes y caras, lineación y foliación en rocas, caras de fricción en los fallos , y otras características lineales y planas. En este contexto, la proyección se llama proyección hemisférica de igual área . También hay una proyección hemisférica de igual ángulo definida por proyección estereográfica . ^[6]

La discusión aquí ha enfatizado el hemisferio inferior z ≤ 0, pero algunas disciplinas prefieren el hemisferio superior z ≥ 0. ^[6] De hecho, cualquier hemisferio puede usarse para registrar las líneas a través del origen en el espacio tridimensional.

Comparación de la proyección acimutal de igual área de Lambert y algunas proyecciones acimutales centradas en 90 ° N en la misma escala, ordenadas por la altitud de proyección en los radios terrestres. (haga clic para más detalles)

Lambert animada proyección [ editar ]

^{[ cita requerida ]}

Animación de una proyección de Lambert. Cada celda de cuadrícula mantiene su área a lo largo de la transformación. En esta animación, los puntos en el ecuador permanecen siempre en el$${\ displaystyle z = 0} avión.

En esta proyección animada de Lambert, el polo sur se mantiene fijo.

Dejar $${\ displaystyle (u, \ phi)} ser dos parámetros para los cuales {\ displaystyle -1  y {\ displaystyle 0 \ leq \ phi <2 font="" pi="">. Dejar$${\ displaystyle H}ser un parámetro de "tiempo" (igual a la altura, o grosor vertical, de la concha en la animación). Si se dibuja una rejilla rectilínea uniforme$${\ displaystyle (u, \ phi)} espacio, entonces cualquier punto en esta cuadrícula se transforma en un punto $${\ displaystyle (x, y, z)} sobre una concha esférica de altura $${\ displaystyle H} segun el mapeo

$${\ displaystyle x = \ lambda (u, H) \ cos (\ phi)}

$${\ displaystyle y = \ lambda (u, H) \ sin (\ phi)}

$${\ displaystyle z = {\ frac {Hu} {2}}}

dónde $${\ displaystyle \ lambda (u, H) = {\ frac {1} {2}} {\ sqrt {(1-u) \ left [8-H ^ {2} (1-u) \ right]}} }. Cada cuadro en la animación corresponde a un diagrama paramétrico de la cuadrícula deformada en un valor fijo de la altura de la concha$${\ displaystyle H}(desde 0 hasta 2). Físicamente,$${\ displaystyle \ lambda} es el estiramiento (longitud deformada dividida por la longitud inicial) de la línea infinitesimal $${\ displaystyle d \ phi}segmentos de linea. Este mapeo se puede convertir en uno que mantiene el polo sur fijo mediante el uso de$${\ displaystyle z = {\ frac {H (1-u)} {2}}.}

Independientemente de los valores de $${\ displaystyle (u, \ phi, H)}, el jacobiano de este mapeo es en todas partes igual a 1, lo que demuestra que de hecho es un mapeo de áreas iguales en toda la animación. Este mapeo generalizado incluye la proyección de Lambert como un caso especial cuando$${\ displaystyle H = 0}.

Aplicación: esta asignación puede ayudar a explicar el significado de una proyección de Lambert al mostrarla para "abrir" la esfera en un polo, transformándola en un disco sin cambiar el área delimitada por celdas de la cuadrícula.