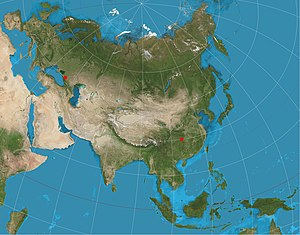
La proyección equidistante de dos puntos es una proyección cartográfica descrita por primera vez por Hans Maurer en 1919. Es una generalización de la proyección equidistante azimutal, mucho más simple . En esta forma de dos puntos, el creador de mapas elige dos puntos de locuspara configurar la proyección. Las distancias desde los dos loci a cualquier otro punto en el mapa son correctas: es decir, se escalan a las distancias de los mismos puntos en la esfera.
La proyección ha sido utilizada para todos los mapas del continente asiático por los atlas de la National Geographic Society desde 1959, [1] aunque su propósito en ese caso era reducir la distorsión en toda Asia en lugar de medir desde los dos loci. [2] La proyección a veces aparece en mapas de rutas aéreas. La proyección trimétrica de Chamberlin es una extensión lógica de la idea de dos puntos a tres puntos, pero el caso de tres puntos solo produce una especie de error mínimo para las distancias de los tres loci, en lugar de proporcionar las distancias correctas. Tobler extendió esta idea a un número arbitrariamente grande de loci mediante el uso de técnicas automatizadas de minimización de la media cuadrática enlugar de usarFórmulas de forma cerrada .
La proyección de van der Grinten es una proyección de mapa de compromiso , lo que significa que no es ni de área igual ni conforme . A diferencia de las proyecciones en perspectiva, la proyección de van der Grinten es una construcción geométrica arbitraria en el plano. Van der Grinten proyecta la Tierra entera en un círculo. Conserva en gran medida las formas familiares de la proyección de Mercator mientras reduce modestamente la distorsión de Mercator. Las regiones polares están sujetas a una distorsión extrema.
Historia [ editar ]
Alphons J. van der Grinten inventó la proyección en 1898 y recibió la patente estadounidense número 751,226 para ella y otras tres en 1904. [2] La National Geographic Society adoptó la proyección para sus mapas de referencia del mundo en 1922, aumentando su visibilidad y estimulando Su adopción en otros lugares. En 1988, National Geographic reemplazó la proyección de van der Grinten con la proyección de Robinson . [1]
Construcción geométrica [ editar ]
La construcción geométrica dada por van der Grinten se puede escribir algebraicamente: [3]
![{\ displaystyle {\ begin {alineado} x & = {\ frac {\ pm \ pi \ left (A \ left (GP ^ {2} \ right) + {\ sqrt {A ^ {2} \ left (GP ^ { 2} \ derecha) ^ {2} - \ izquierda (P ^ {2} + A ^ {2} \ derecha) \ izquierda (G ^ {2} -P ^ {2} \ derecha)}} \ derecha)} {P ^ {2} + A ^ {2}}} \\ [5px] y & = {\ frac {\ pm \ pi \ left (PQ-A {\ sqrt {\ left (A ^ {2} +1 \ derecha) \ izquierda (P ^ {2} + A ^ {2} \ derecha) -Q ^ {2}}} \ derecha)} {P ^ {2} + A ^ {2}}} \ fin {alineado} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/919df2ba8d83552abc081b4801ea63d03493341f)
donde x toma el signo de λ - λ 0 , y toma el signo de φ y
![{\ displaystyle {\ begin {alineado} A & = {\ frac {1} {2}} \ left | {\ frac {\ pi} {\ lambda - \ lambda _ {0}}} - {\ frac {\ lambda - \ lambda _ {0}} {\ pi}} \ right | \\ [5px] G & = {\ frac {\ cos \ theta} {\ sin \ theta + \ cos \ theta -1}} \\ [5px ] P & = G \ left ({\ frac {2} {\ sin \ theta}} - 1 \ right) \\ [5px] \ theta & = \ arcsin \ left | {\ frac {2 \ varphi} {\ pi }} \ right | \\ [5px] Q & = A ^ {2} + G \ end {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ca04b79ef02f10bdc7c0c918e082ef7754a13b1)
Si φ = 0, entonces
De manera similar, si λ = λ 0 o φ = ± π2 , entonces
En todos los casos, φ es la latitud , λ es la longitud y λ 0 es el meridiano central de la proyección.
Wagner VI es una proyecciónpseudocilíndrica de la Tierra entera . Al igual que la proyección de Robinson , es una proyección de compromiso, que no tiene ningún atributo especial que no sea una apariencia agradable y de baja distorsión. Wagner VI es equivalente al Kavrayskiy VIIalargado horizontalmente por un factor de⁄. Esta elongación da como resultado la conservación adecuada de las formas cerca del ecuador, pero una distorsión general ligeramente mayor. La relación de aspecto de esta proyección es de 2: 1, según lo formado por la relación del ecuador al meridiano central. Esto hace coincidir la relación del ecuador de la Tierra con cualquier meridiano.
El Wagner VI se define por: [1]
.jpg)
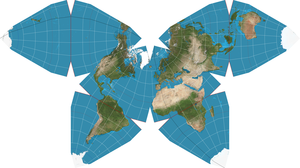
El Mapa Mundial de Waterman "Mariposa" es un arreglo de mapa creado por Steve Waterman . Waterman publicó por primera vez un mapa en este arreglo en 1996. El despliegue es un despliegue de un globo tratado como un octaedro truncado , que evoca el principio del mapa de la mariposa desarrollado por Bernard JS Cahill (1866–1944) en 1909. Los mapas de Cahill y Waterman pueden ser se muestra en varios perfiles, típicamente vinculados en los océanos del Pacífico norte o Atlántico norte .
Como Cahill era un arquitecto , su enfoque tendía hacia formas que se podían demostrar físicamente, como por ejemplo su mapa de bolas de goma aplastable. Waterman, por otro lado, derivó su diseño de su trabajo en el empaquetado de esferas . Esto implica conectar los centros de la esfera de las esferas cúbicas más cercanas en un casco convexo correspondiente, como se muestra en los gráficos adjuntos. Estos ilustran el grupo de esferas W5, el casco convexo W5 y dos proyecciones Waterman del casco convexo W5.
Para proyectar la esfera al poliedro, la Tierra se divide en ocho octantes . Cada meridiano se dibuja como tres segmentos de línea recta en su octante respectivo , cada segmento definido por sus puntos finales en dos de las cuatro "Delineaciones de línea igual" definidas por Waterman. Estas Delineaciones de Línea Igual son el Polo Norte , el borde del poliedro más septentrional, la línea más larga paralela al ecuador y el ecuador en sí. Las intersecciones de todos los meridianos con cualquier Delineación de Línea Igual están espaciadas por igual, y las intersecciones de todos los paralelos con cualquier meridiano están igualmente espaciadas. [1]Waterman eligió el poliedro Waterman W5 y el meridiano central de 20 ° W para minimizar la interrupción de las masas terrestres principales. Popko observa que la proyección también puede ser gnomónica. [2] Los dos métodos producen resultados muy similares.
Al igual que la Proyección Dymaxion de Buckminster Fuller en 1943 , un mapa octaédrico de mariposas puede mostrar todos los continentes ininterrumpidos si sus octantes se dividen en un meridiano adecuado (en este caso 20 ° W) y se unen, por ejemplo, en el Atlántico Norte, como en La versión de 1996.
No hay comentarios:
Publicar un comentario