PROYECCIONES DE MAPAS

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Proyección de Cassini del mundo.

Proyección de cassini con indicatrices de 1.000 km.

Cassini proyección del mundo modela como un elipsoide achatado altamente con aplanamiento 1: 2 (= excentricidad ^√ 3 / ₂ )

La proyección de Cassini (también conocida a veces como proyección de Cassini-Soldner o proyección de Soldner ^[1] ) es una proyección de mapa descrita por César-François Cassini de Thury en 1745. ^[2] Es el aspecto transversal de la proyección equirectangular , en eso primero se gira el globo para que el meridiano central se convierta en el "ecuador" y luego se aplique la proyección equirectangular normal. Considerando la tierra como una esfera, la proyección se compone de las operaciones:

$${\ displaystyle x = \ arcsin (\ cos \ varphi \ sin \ lambda) \ qquad y = \ arctan \ left ({\ frac {\ tan \ varphi} {\ cos \ lambda}} \ right).}

donde λ es la longitud del meridiano central y φ es la latitud. Cuando se programan estas ecuaciones, la función tangente inversa utilizada es en realidad la función atan2 , con el primer argumento sin  φ ) y el segundo cos φ cos λ .

La operación inversa se compone de las operaciones:

$${\ displaystyle \ varphi = \ arcsin (\ sin y \ cos x) \ qquad \ lambda = \ operatorname {atan2} (\ tan x, \ cos y).}

En la práctica, la proyección siempre se ha aplicado a los modelos de la tierra como un elipsoide , lo que complica enormemente el desarrollo matemático, pero es adecuado para la topografía. Sin embargo, el uso de la proyección Cassini ha sido superado en gran medida por la proyección transversal de Mercator , al menos con las agencias cartográficas centrales.

Distorsiones [ editar ]

Las áreas a lo largo del meridiano central, y en ángulo recto con él, no están distorsionadas. En otros lugares, la distorsión es mayormente en dirección norte-sur, y varía según el cuadrado de la distancia desde el meridiano central. Como tal, cuanto mayor es la extensión longitudinal del área, peor se vuelve la distorsión.

Debido a esto, la proyección Cassini funciona mejor en áreas largas y estrechas, y peor en áreas amplias.

Forma elíptica [ editar ]

La cassini se conoce como proyección esférica, pero puede generalizarse como una forma elíptica.

Considerando la tierra como una elipse, la proyección se compone de estas operaciones:

$${\ displaystyle N = (1-e ^ {2} \ sin ^ {2} \ varphi) ^ {- 1/2}}

$${\ displaystyle T = \ tan ^ {2} \ varphi}

$${\ displaystyle A = \ lambda \ cos \ varphi}

$${\ displaystyle C = {\ frac {e ^ {2}} {1-e ^ {2}}} \ cos ^ {2} \ varphi}

$${\ displaystyle x = N \ left (AT {\ frac {A ^ {3}} {6}} - (8-T + 8C) T {\ frac {A ^ {5}} {120}} \ right) }

$${\ displaystyle y = M (\ varphi) -M (\ varphi _ {0}) + (N \ tan \ varphi) \ left ({\ frac {A ^ {2}} {2}} + (5-T + 6C) {\ frac {A ^ {4}} {24}} \ derecha)}

y M es la función de distancia meridional .

La operación inversa se compone de las operaciones:

$${\ displaystyle \ varphi '= M ^ {- 1} (M (\ varphi _ {0}) + y)}

Si $${\ displaystyle \ varphi '= {\ frac {\ pi} {2}}} entonces $${\ displaystyle \ varphi = \ varphi '} y $${\ displaystyle \ lambda = 0.}

De lo contrario calcule T y N como arriba con$${\ displaystyle \ varphi '}y

$${\ displaystyle R = (1-e ^ {2}) (1-e ^ {2} \ sin ^ {2} \ varphi ') ^ {- 3/2}}

$${\ displaystyle D = x / N}

$${\ displaystyle \ varphi = \ varphi '- {\ frac {N \ tan \ varphi'} {R}} \ left ({\ frac {D ^ {2}} {2}} - (1 + 3T) {\ frac {D ^ {4}} {24}} \ derecha)}

$${\ displaystyle \ lambda = {\ frac {DT {\ frac {D ^ {3}} {3}} + (1 + 3T) T {\ frac {D ^ {5}} {15}}} {\ cos \ varphi '}}}

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

La proyección cilíndrica central con una retícula de 15 °, aproximadamente a latitud ± 72 °. La distorsión es notablemente peor que la proyección de Mercator .

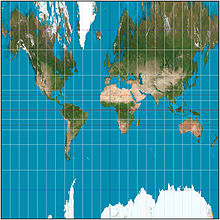
La proyección cilíndrica central es una perspectiva proyección de mapa cilíndrico . Corresponde a proyectar la superficie de la Tierra sobre un cilindro tangente al ecuador como si fuera una fuente de luz en el centro de la Tierra. Luego, el cilindro se corta a lo largo de uno de los meridianos proyectados y se desenrolla en un mapa plano. ^[1]

La distorsión aumenta tan rápidamente fuera del ecuador que la cilíndrica central solo se usa como una ilustración de proyección fácil de entender, en lugar de para mapas prácticos. ^[1] Su estiramiento vertical es incluso mayor que el de la proyección de Mercator , cuyo método de construcción a veces se describe erróneamente de manera equivalente a la cilíndrica central. ^[2] No se sabe quién desarrolló la proyección por primera vez, pero apareció con otras proyecciones cilíndricas nuevas en el siglo XIX, y regularmente encuentra su camino en los libros de texto, principalmente para ilustrar que esta no es la forma en que se construye Mercator. ^[1] Como con cualquier proyección cilíndrica, la construcción puede generalizarse colocando el cilindro para que sea tangente a unGran circulo del globo que no es el ecuador. ^[1]

Esta proyección tiene un uso prominente en la fotografía panorámica, donde generalmente se llama "proyección cilíndrica". Puede presentar un panorama completo de 360 ​​° y preservar las líneas verticales. A diferencia de otras proyecciones cilíndricas, proporciona una perspectiva correcta para objetos altos, un rasgo importante para las escenas arquitectónicas.

Fórmulas [ editar ]

$${\ displaystyle x = R \ left (\ lambda - \ lambda _ {0} \ right), \ qquad y = R \ tan \ varphi}

R denota el radio del globo generador; φ es la latitud; λ es la longitud; λ ₀ es la longitud del meridiano central; y xy y son las coordenadas mapeadas.

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Un mapa de África usando la proyección trimétrica de Chamberlin. Los tres puntos rojos indican las ubicaciones "base" seleccionadas: (22 ° N, 0 °), (22 ° N, 45 ° E), (22 ° S, 22.5 ° E). 10 ° gratícula .

La proyección trimétrica de Chamberlin es una proyección de mapa donde se fijan tres puntos en el globo terráqueo y los puntos en la esfera se mapean en un plano mediante triangulación . Fue desarrollado en 1946 por Wellman Chamberlin para la National Geographic Society . ^[1] Chamberlin fue cartógrafo jefe de la Sociedad desde 1964 hasta 1971. ^[2] La característica principal de la proyección es que compromete las distorsiones de área, dirección y distancia. Un mapa trimétrico de Chamberlin, por lo tanto, brinda un excelente sentido general de la región que se está mapeando. ^[3] MuchosLos mapas de la National Geographic Society de los continentes individuales utilizan esta proyección. ^[2]

Como se implementó originalmente, el algoritmo deproyección comienza con la selección de tres puntos cerca del límite exterior del área a ser mapeada. A partir de estos tres puntos base, se calculan las distancias reales a un punto en el área de mapeo. Las distancias de cada uno de los tres puntos base se dibujan en el plano mediante círculos de brújula. A diferencia de la triangulación en un plano en el que tres de estos círculos de la brújula se intersecarán en un punto único, los círculos de la brújula de una esfera no se intersecarán precisamente en un punto. Se genera un pequeño triángulo a partir de las intersecciones, y el centro de este triángulo se calcula como el punto mapeado. ^[1]

Un mapa de proyección trimétrica de Chamberlin se obtuvo originalmente mediante el mapeo gráfico de los puntos a intervalos regulares de latitud y longitud , con líneas costeras y otras características que luego se mapearon por interpolación. Sobre la base de los principios de la proyección, se desarrollaron posteriormente fórmulas matemáticas precisas, pero extensas, para calcular esta proyección por computadora para una tierra esférica . ^{[2] [3] [4]}

La proyección trimétrica de Chamberlin no es conforme ni de área igual . Más bien, la proyección fue concebida para minimizar la distorsión de las distancias en todas partes con el efecto secundario de equilibrar la equivalencia entre áreas y la conformidad. ^[3] Esta proyección no es apropiada para mapear toda la esfera porque el límite exterior se enroscaría y se superpondría en la mayoría de las configuraciones.