La proyección equidistante azimutal es una proyección de mapa azimutal . Tiene las propiedades útiles de que todos los puntos en el mapa están a distancias proporcionalmente correctas del punto central, y que todos los puntos en el mapa están en el acimut correcto (dirección) desde el punto central. Una aplicación útil para este tipo de proyección es una proyección polar que muestra todos los meridianos (líneas de longitud) como rectos, con las distancias desde el polo representadas correctamente. La bandera de las Naciones Unidas contiene un ejemplo de una proyección equidistante azimutal polar.
Historia [ editar ]
Si bien los antiguos egipcios lo utilizaron para los mapas estelares en algunos libros sagrados, [1] el texto más antiguo que describe la proyección equidistante azimutal es una obra de al-Biruni del siglo XI . [2]
La proyección aparece en muchos mapas del Renacimiento, y Gerardus Mercator lo usó para un recuadro de las regiones del polo norte en la hoja 13 y la leyenda 6 de su conocido mapa 1569 . En Francia y Rusia, esta proyección se denomina "proyección de Postel", en honor de Guillaume Postel , quien la usó para un mapa en 1581. [3] Muchas planisferias modernas de los mapas estelares utilizan la proyección equidistante azimutal polar.
Definición matemática [ editar ]
Se elige un punto del globo para que sea especial en el sentido de que las distancias y los acimuts asignados desde ese punto a cualquier otro punto serán correctos. Ese punto, ( φ 1 , λ 0 ), se proyectará al centro de una proyección circular, con φ que se refiere a la latitud y λ a la longitud. Todos los puntos a lo largo de un acimut dado se proyectarán a lo largo de una línea recta desde el centro, y el ángulo θ que la línea subtiende de la vertical es el ángulo del acimut. La distancia desde el punto central a otro punto proyectado se da como ρ . Por esta descripción, entonces, el punto en el plano especificado por ( θ , ρ) se proyectarán a coordenadas cartesianas:
La relación entre las coordenadas ( θ , ρ ) del punto en el globo, y sus coordenadas de latitud y longitud ( φ , λ ) se encuentra de la siguiente manera. La gran distancia de círculo ρ entre dos puntos ( φ 1 , λ 0 ) y ( φ , λ ) en la esfera viene dada por: [4]
El acimut del primer al segundo punto viene dado por:
Cuando el punto central es el polo norte, estas fórmulas se simplifican enormemente a:
Aplicaciones [ editar ]
En el caso de la radio, esta proyección permite la orientación de la antena direccional , especialmente en el caso de las comunicaciones por ondas decamétricas . Un operador puede apuntar la antena, generalmente con un rotador eléctrico , simplemente ubicando el objetivo en el mapa y girando la antena al ángulo indicado por el mapa. El mapa debe estar centrado lo más cerca posible de la ubicación real de la antena.
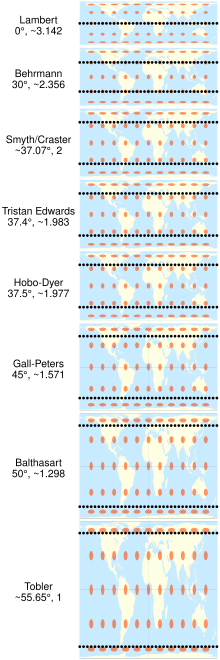
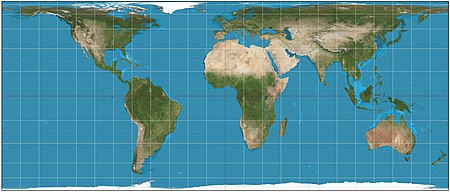
La proyección de Behrmann es una proyección de mapa cilíndricadescrita por Walter Behrmann en 1910. Es un miembro de la familia de proyecciones cilíndricas de igual área . Los miembros de la familia difieren por sus paralelos estándar, que son paralelos a lo largo de los cuales la proyección no tiene distorsión. En el caso de la proyección de Behrmann, los paralelos estándar son 30 ° N y 30 ° S. La proyección comparte muchas características con otros miembros de la familia, como la proyección cilíndrica de igual área de Lambert , cuyo paralelo estándar es el ecuador, y la proyección Gall-Peters, cuyos paralelos estándar son 45 ° N y 45 ° S. Mientras que la zona es igual, la distorsión de la forma aumenta en la proyección de Behrmann de acuerdo con la distancia de los paralelos estándar. Esta proyección no es equidistante .










No hay comentarios:
Publicar un comentario