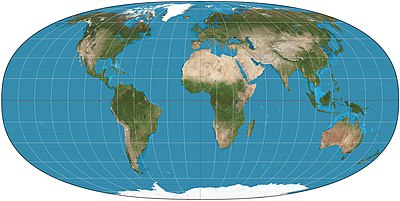
La proyección Strebe 1995 , la proyección Strebe, Strebe lenticular proyección de áreas equivalentes , o Strebe de áreas equivalentes proyección cónica múltiple es una proyección del mapa de áreas equivalentes presentado por Daniel "Daan" Strebe en 1994. Strebe diseñado la proyección para mantener todas las áreas y proporciones correctas en tamaño; para alejar lo más posible de la inevitable distorsión de las masas continentales hacia el Océano Pacífico; mantener una orientación ecuatorial familiar; Y hacer todo esto sin cortar el mapa.
Descripción [ editar ]
Strebe presentó la proyección por primera vez en una reunión conjunta de la Asociación Cartográfica Canadiense y la Sociedad de Información Cartográfica de América del Norte (NACIS) en agosto de 1994. [2] Su formulación final se completó en 1995. La proyección ha estado disponible en el software de proyección de mapas Geocart desde Geocart 1.2, lanzado en octubre de 1994. [3]
Se llega a la proyección mediante una serie de pasos, cada uno de los cuales preserva áreas. Debido a que cada paso preserva áreas, todo el proceso preserva áreas. Los pasos utilizan una técnica inventada por Strebe llamada "deproyección sustituta" [3] o "transformación de Strebe". [4] Primero, se computa la proyección Eckert IV . Luego, simulando que la proyección Eckert es en realidad una parte reducida de la proyección Mollweide , el Eckert se "desproyecta" nuevamente en la esfera mediante la transformación inversa de la proyección Mollweide. Esto produce un mapa de esfera completa a esfera parcial. Luego, esta esfera asignada se proyecta de nuevo al plano utilizando la proyección Hammer. Si bien las proyecciones aquí mencionadas son las que definen la proyección de Strebe 1995, el principio de deproyección sustitutivo no está limitado a proyecciones particulares.
La proyección que se describe se puede formular de la siguiente manera: [3]
dónde Se resuelve iterativamente:
En estas fórmulas, representa la longitud y representa la latitud
Arreglo preferido de Strebe es establecer , como se muestra, y 11 ° E como el meridiano central para evitar dividir la península de Chukchi en Siberia oriental . Sin embargo, s puede modificarse para cambiar la apariencia sin destruir la propiedad de área de igualdad.
La proyección hiperelíptica de Tobler es una familia de proyecciones pseudocilíndricas de áreas iguales que se pueden usar para mapas mundiales . Waldo R. Tobler introdujo la construcción en 1973 como la proyección hiperelíptica , ahora conocida generalmente como la proyección hiperelíptica Tobler. [1]
Descripción general [ editar ]
Al igual que con cualquier proyección pseudocilíndrica, en el aspecto normal de la proyección, [2] los paralelos de latitud son líneas paralelas y rectas . Su espaciado se calcula para proporcionar la propiedad de igual área. La proyección combina la proyección cilíndrica de áreas iguales con meridianos de longitud que siguen un tipo particular de curva conocida como superelipses [3] o curvas de Lamé o, a veces, como hiperelipses. La curva se describe por x k + y k = γ k. El peso relativo de la proyección cilíndrica de igual área se da como α , que va desde toda área cilíndrica igual con α = 1 a todas las hiperelipses con α = 0.
Cuando α = 0 yk = 1, la proyección degenera a la proyección de Collignon ; cuando α = 0, k = 2 y γ ≈ 1.2731 la proyección se convierte en la proyección de Mollweide . [4] Tobler favoreció la parametrización mostrada con la ilustración superior; es decir, α = 0, k = 2.5 y γ = 1.183136.
La proyección del mapa de Mercator transversal es una adaptación de la proyección estándar de Mercator . La versión transversal se usa ampliamente en los sistemas de cartografía nacionales e internacionales de todo el mundo, incluida la UTM . Cuando se combina con un dato geodésico adecuado , el Mercator transversal ofrece una alta precisión en zonas de menos de unos pocos grados en la extensión este-oeste.
Standard y aspectos transversales [ editar ]
La proyección de Mercator transversal es el aspecto transversal de la proyección de Mercator estándar (o Normal). Comparten la misma construcción matemática subyacente y, en consecuencia, el Mercator transversal hereda muchos rasgos del Mercator normal:
- Ambas proyecciones son cilíndricas : para el Mercator normal, el eje del cilindro coincide con el eje polar y la línea de tangencia con el ecuador. Para el Mercator transversal, el eje del cilindro se encuentra en el plano ecuatorial, y la línea de tangencia es cualquier meridiano elegido, designado de este modo el meridiano central .
- Ambas proyecciones pueden modificarse a formas secantes, lo que significa que la escala se ha reducido para que el cilindro se deslice a través del globo del modelo.
- Ambos existen en versiones esféricas y elipsoidales .
- Ambas proyecciones son conformes , por lo que la escala de puntos es independiente de la dirección y lasformas locales están bien conservadas;
- Ambas proyecciones tienen una escala constante en la línea de tangencia (el ecuador para el Mercator normal y el meridiano central para el transversal).
Dado que el meridiano central del Mercator transversal se puede elegir a voluntad, se puede usar para construir mapas altamente precisos (de ancho estrecho) en cualquier parte del globo. La forma secante y elipsoidal del Mercator transversal es la más ampliamente aplicada de todas las proyecciones para obtener mapas precisos a gran escala.
Mercator esférico transversal [ editar ]
Al construir un mapa en cualquier proyección, normalmente se elige una esfera para modelar la Tierra cuando la extensión de la región mapeada excede unos pocos cientos de kilómetros de longitud en ambas dimensiones. Para mapas de regiones más pequeñas, se debe elegir un modelo elipsoidal si se requiere una mayor precisión; Vea la siguiente sección. La forma esférica de la proyección de Mercator transversal fue una de las siete nuevas proyecciones presentadas, en 1772, por Johann Heinrich Lambert . [1] [2] (El texto también está disponible en una traducción al inglés moderno. [3] ) Lambert no mencionó sus proyecciones; El nombre de Mercator transversedata de la segunda mitad del siglo XIX. [4] Las principales propiedades de la proyección transversal se presentan aquí en comparación con las propiedades de la proyección normal.
Proyecciones esféricas normales y transversales [ editar ]
| Mercator normal | Mercator Transversal | |||
|---|---|---|---|---|
| • | El meridiano central se proyecta a la línea recta x = 0. Otros meridianos se proyectan a líneas rectas con x constante. | • | El meridiano central se proyecta a la línea recta x = 0. Los meridianos 90 grados al este y al oeste del meridiano central proyectan líneas constantes y através de los polos proyectados. Todos los demás meridianos se proyectan a curvas complicadas. | |
| • | El ecuador proyecta a la recta y = 0 y los círculos paralelos proyectan a rectas de constante y . | • | El ecuador se proyecta a la línea recta y = 0, pero todos los demás paralelos son curvas cerradas complicadas. | |
| • | Los meridianos y paralelos proyectados se intersecan en ángulos rectos. | • | Los meridianos y paralelos proyectados se intersecan en ángulos rectos. | |
| • | La proyección es ilimitada en la dirección y . Los polos se encuentran en el infinito. | • | La proyección es ilimitada en la dirección x . Los puntos en el ecuador a noventa grados del meridiano central se proyectan hasta el infinito. | |
| • | La proyección es conforme. Las formas de los pequeños elementos están bien conservadas. | • | La proyección es conforme. Las formas de los pequeños elementos están bien conservadas. | |
| • | La distorsión aumenta con y . La proyección no es adecuada para los mapas del mundo. La distorsión es pequeña cerca del ecuador y la proyección (particularmente en su forma elipsoidal) es adecuada para el mapeo preciso de las regiones ecuatoriales. | • | La distorsión aumenta con x . La proyección no es adecuada para los mapas del mundo. La distorsión es pequeña cerca del meridiano central y la proyección (particularmente en su forma elipsoidal) es adecuada para el mapeo preciso de regiones estrechas. | |
| • | Groenlandia es casi tan grande como África; el área real es aproximadamente una decimotercera la de África. | • | Groenlandia y África están cerca del meridiano central; sus formas son buenas y la proporción de las áreas es una buena aproximación a los valores reales. | |
| • | El factor de escala de puntos es independiente de la dirección. Es una función de y en la proyección.(En la esfera solo depende de la latitud). La escala es verdadera en el ecuador. | • | El factor de escala de puntos es independiente de la dirección. Es una función de x en la proyección.(En la esfera depende tanto de la latitud como de la longitud). La escala es verdadera en el meridiano central. | |
| • | La proyección es razonablemente precisa cerca del ecuador. La escala a una distancia angular de 5 ° (en latitud) alejada del ecuador es menos de 0.4% mayor que la escala en el ecuador, y es aproximadamente 1.54% mayor a una distancia angular de 10 °. | • | La proyección es razonablemente precisa cerca del meridiano central. La escala a una distancia angular de 5 ° (en longitud) alejada del meridiano central es menos de 0.4% mayor que la escala en el meridiano central, y es aproximadamente 1.54% a una distancia angular de 10 °. | |
| • | En la versión secante, la escala se reduce en el ecuador y es verdadera en dos líneas paralelas al ecuador proyectado (y corresponde a dos círculos paralelos en la esfera). | • | En la versión secante, la escala se reduce en el meridiano central y es verdadera en dos líneas paralelas al meridiano central proyectado. (Las dos líneas no son meridianos.) | |
| • | La convergencia (el ángulo entre los meridianos proyectados y las líneas de cuadrícula con xconstante) es idénticamente cero. Cuadrícula norte y norte verdadero coinciden. | • | La convergencia es cero en el ecuador y no cero en cualquier otra parte. Aumenta a medida que se acercan los polos. Grid norte y norte verdadero no coinciden. | |
| • | Las líneas de trazos (de acimut constante en la esfera) se proyectan en líneas rectas. | • | Las líneas de rumbo se proyectan a curvas complejas. |
Elipsoidal transversal Mercator [ editar ]
La forma elipsoidal de la proyección de Mercator transversal fue desarrollada por Carl Friedrich Gauss en 1825 [5]y posteriormente analizada por Johann Heinrich Louis Krüger en 1912. [6] La proyección es conocida por varios nombres: Gauss Conformal o Gauss-Krüger en Europa; el Mercator transverso en Estados Unidos; o Gauss-Krüger Mercator transversal en general. La proyección es conforme a una escala constante en el meridiano central. (Hay otras generalizaciones conformes del Mercator transverso desde la esfera hasta el elipsoide, pero solo Gauss-Krüger tiene una escala constante en el meridiano central). A lo largo del siglo XX, el Mercator transverso de Gauss-Krüger fue adoptado, de una forma u otra, por muchas naciones (y organismos internacionales);[7] además, proporciona la base para laserie de proyecciones Universal Mercator Transversal . La proyección de Gauss-Krüger es ahora la proyección más utilizada en el mapeo preciso a gran escala. [ cita requerida ]
La proyección, tal como fue desarrollada por Gauss y Krüger, se expresó en términos de series de poder de bajo orden que se suponía divergían en la dirección este-oeste, exactamente como en la versión esférica. El cartógrafo británico EH Thompson demostró que esto no es cierto, cuya versión no publicada (versión cerrada) de la proyección, publicada por LP Lee en 1976, [8] mostró que la proyección elipsoidal es finita (a continuación). Esta es la diferencia más llamativa entre las versiones esféricas y elipsoidales de la proyección de Mercator transversal: Gauss-Krüger ofrece una proyección razonable de todo el elipsoide al plano, aunque su aplicación principal es el mapeo a gran escala preciso "cercano" a la central. meridiano. [ cita requerida ]
Características [ editar ]
- Cerca del meridiano central (Greenwich en el ejemplo anterior), la proyección tiene baja distorsión y las formas de África, Europa occidental, las Islas Británicas, Groenlandia y la Antártida se comparan favorablemente con un globo.
- Las regiones centrales de las proyecciones transversales en esfera y elipsoide son indistinguibles en las proyecciones a pequeña escala que se muestran aquí.
- Los meridianos a 90 ° este y oeste del meridiano central elegido se proyectan a líneas horizontales a través de los polos. El hemisferio más distante se proyecta sobre el polo norte y debajo del polo sur.
- El ecuador divide África, cruza Sudamérica y luego continúa hasta el límite exterior completo de la proyección; los bordes superior e inferior y los bordes derecho e izquierdo deben identificarse (es decir, representan las mismas líneas en el globo). (Indonesia está dividida en dos).
- La distorsión aumenta hacia los límites derecho e izquierdo de la proyección, pero no aumenta hasta el infinito. Tenga en cuenta las Islas Galápagos, donde el meridiano 90 ° oeste se encuentra con el ecuador en la parte inferior izquierda.
- El mapa es conforme. Líneas que se intersecan en cualquier ángulo especificado en el proyecto elipsoidal en líneas que se intersecan en el mismo ángulo en la proyección. En particular, los paralelos y meridianos se intersecan a 90 °.
- El factor de escala de puntos es independiente de la dirección en cualquier punto, de modo que la forma de una pequeña región se encuentre razonablemente bien conservada. La condición necesaria es que la magnitud del factor de escala no debe variar demasiado en la región en cuestión. Tenga en cuenta que si bien América del Sur está muy distorsionada, la isla de Ceilán es lo suficientemente pequeña como para tener una forma razonable, aunque está lejos del meridiano central.
- La elección del meridiano central afecta grandemente la apariencia de la proyección. Si se elige 90 ° W, entonces el conjunto de las Américas es razonable. Si se elige 145 ° E, el Lejano Oriente es bueno y Australia está orientada hacia el norte.
En la mayoría de las aplicaciones, el sistema de coordenadas de Gauss-Krüger se aplica a una franja estrecha cerca de los meridianos centrales, donde las diferencias entre las versiones esféricas y elipsoidales son pequeñas, pero sin embargo son importantes para el mapeo preciso. Las series directas para escala, convergencia y distorsión son funciones de la excentricidad y tanto de latitud como de longitud en el elipsoide: las series inversas son funciones de la excentricidad y tanto de x como de y en la proyección. En la versión secante, las líneas de escala real en la proyección ya no son paralelas al meridiano central; se curvan ligeramente. El ángulo de convergencia entre los meridianos proyectados y la xlas líneas de cuadrícula constantes ya no son cero (excepto en el ecuador), por lo que un rumbo de la cuadrícula debe corregirse para obtener un azimut del norte verdadero. La diferencia es pequeña, pero no despreciable, particularmente en latitudes altas.
Implementaciones de la proyección de Gauss-Krüger [ editar ]
En su artículo de 1912 [6] , Krüger presentó dos soluciones distintas, distinguidas aquí por el parámetro de expansión:
- Krüger- n (párrafos 5 a 8): fórmulas para la proyección directa, dando las coordenadas x y y , son cuarto expansiones orden en términos de la tercera aplanamiento, n (la relación de la diferencia y suma de los ejes mayor y menor de el elipsoide). Los coeficientes se expresan en términos de latitud ( φ ), longitud ( λ ), eje mayor ( a ) y excentricidad ( e ). Las fórmulas inversas para φ y λ también son expansiones de cuarto orden en n pero con coeficientes expresados en términos de x , y , a ye .
- Krüger- λ (párrafos 13 y 14): Fórmulas que dan la proyección coordenadas x y Y son expansiones (de órdenes 5 y 4 respectivamente) en términos de la longitud λ , expresados en radianes: los coeficientes se expresan en términos de φ , una y e . La proyección inversa para φ y λ son expansiones de sexto orden en términos de la relación xa , con coeficientes expresados en términos de y , a y e . (Ver la serie de Mercator Transversal: Redfearn .)
Las series Krüger- λ fueron las primeras en implementarse, posiblemente porque fueron mucho más fáciles de evaluar en las calculadoras manuales de mediados del siglo XX.
- Lee – Redfearn – OSGB : en 1945, LP Lee [9] confirmó las expansiones de Krüger en λ y propuso su adopción por parte de OSGB [10], pero Redfearn (1948) [11] señaló que no eran exactas debido a (a) las latitudes relativamente altas de Gran Bretaña y (b) el gran ancho del área mapeada, más de 10 grados de longitud. Redfearn extendió la serie a octavo orden y examinó qué términos eran necesarios para alcanzar una precisión de 1 mm (medición en el suelo). Las series de Redfearn siguen siendo la base de las proyecciones de mapas OSGB. [10]
- Thomas – UTM : Las expansiones en λ de Krüger también fueron confirmadas por Paul Thomas en 1952: [12]están disponibles en Snyder. [13] Sus fórmulas de proyección, completamente equivalentes a las presentadas por Redfearn, fueron adoptadas por la Agencia de Mapas de Defensa de los Estados Unidos como la base para la UTM . [14] También se incorporan al convertidor de coordenadas Geotrans [15] disponible por la Agencia Nacional de Inteligencia Geoespacial de los Estados Unidos [3] .
- Otros países : la serie Redfearn es la base para el mapeo geodésico en muchos países: Australia, Alemania, Canadá, Sudáfrica, por nombrar solo algunos. (Se proporciona una lista en el Apéndice A.1 de Stuifbergen 2009.) [16]
- Se han propuesto muchas variantes de la serie Redfearn, pero solo las adoptadas por las agencias cartográficas nacionales son importantes. Para ver un ejemplo de modificaciones que no tienen este estado, consulte Mercator transversal: serie Bowring ). Todas estas modificaciones han sido eclipsadas por el poder de las computadoras modernas y el desarrollo de la serie n de alto orden que se describe a continuación. La serie precisa de Redfearn, aunque de bajo orden, no puede ser ignorada, ya que todavía están consagradas en las definiciones cuasi legales de OSGB y UTM, etc.
Las siguientes naciones han implementado la serie Krüger – n (cuarto orden en n ).
Las versiones de orden superior de la serie Krüger – n han sido implementadas en séptimo orden por Ensager y Poder [21] y en décimo orden por Kawase. [22] Además de una expansión de la serie para la transformación entre latitud y latitud conforme, Karney ha implementado la serie en el trigésimo orden. [23]
Exact Gauss-Krüger y precisión de la serie truncada [ editar ]
LP Lee describe una solución exacta de EH Thompson. [8] Se construye en términos de funciones elípticas (definidas en los capítulos 19 y 22 del manual NIST [24] ) que pueden calcularse con precisión arbitraria utilizando sistemas de cálculo algebraico como Maxima. [25] Tal implementación de la solución exacta está descrita por Karney (2011). [23]
La solución exacta es una herramienta valiosa para evaluar la precisión de las series n y λ truncadas . Por ejemplo, la serie original de 1912 Krüger – n se compara muy favorablemente con los valores exactos: difieren en menos de 0,31 μm dentro de 1000 km del meridiano central y en menos de 1 mm hasta 6000 km. Por otro lado, la diferencia de la serie Redfearn utilizada por Geotrans y la solución exacta es inferior a 1 mm a una diferencia de longitud de 3 grados, que corresponde a una distancia de 334 km desde el meridiano central en el ecuador, pero solo 35 Km. en el límite norte de una zona UTM. Por lo tanto, la serie Krüger – n es mucho mejor que la serie Redfearn λ.
La serie Redfearn empeora a medida que la zona se ensancha. Karney habla de Groenlandia como un ejemplo instructivo. La masa terrestre delgada y larga se centra en 42W y, en su punto más ancho, no está a más de 750 km de ese meridiano, mientras que el tramo en longitud alcanza casi 50 grados. Krüger– n tiene una precisión de 1 mm, pero la versión Redfearn de la serie Krüger– λ tiene un error máximo de 1 kilómetro.
La serie de 8º orden (en n ) de Karney tiene una precisión de 5 nm dentro de los 3900 km del meridiano central.
Fórmulas para el Mercator esférico transversal [ editar ]
Mercator normal esférico revisado [ editar ]
Las proyecciones cilíndricas normales se describen en relación con un cilindro tangencial en el ecuador con un eje a lo largo del eje polar de la esfera. Las proyecciones cilíndricas se construyen de manera que todos los puntos de un meridiano se proyecten a puntos con x = aλ e y una función prescrita de φ . Para una proyección de Mercator normal tangente, las fórmulas (únicas) que garantizan la conformidad son: [26]
![{\ displaystyle x = a \ lambda \ ,, \ qquad y = a \ ln \ left [\ tan \ left ({\ frac {\ pi} {4}} + {\ frac {\ varphi} {2}} \ derecha) \ derecha] = {\ frac {a} {2}} \ ln \ izquierda [{\ frac {1+ \ sin \ varphi} {1- \ sin \ varphi}} \ derecha].](https://wikimedia.org/api/rest_v1/media/math/render/svg/47d199db07fc6cb9a3994a7f82e29c99382ca7dd)
La conformidad implica que la escala de puntos , k , es independiente de la dirección: es una función de la latitud solamente:
Para la versión secante de la proyección, hay un factor de k 0 en el lado derecho de todas estas ecuaciones: esto asegura que la escala sea igual a k 0 en el ecuador.
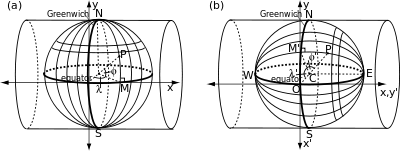
Retículas normales y transversales [ editar ]
La figura de la izquierda muestra cómo se relaciona un cilindro transversal con la retícula convencional en la esfera. Es tangencial a un meridiano elegido arbitrariamente y su eje es perpendicular al de la esfera. Los ejes xe y definidos en la figura están relacionados con el ecuador y el meridiano central exactamente como lo son para la proyección normal. En la figura de la derecha, una retícula rotada se relaciona con el cilindro transversal de la misma manera que el cilindro normal se relaciona con la retícula estándar. El 'ecuador', los 'polos' (E y W) y los 'meridianos' de la retícula rotada se identifican con el meridiano central elegido, los puntos en el ecuador 90 grados al este y al oeste del meridiano central, y los grandes círculos a través de esos puntos.
La posición de un punto arbitrario ( φ , λ ) en la retícula estándar también se puede identificar en términos de ángulos en la retícula rotada: φ ′(ángulo M′CP) es una latitud efectiva y - λ ′ (ángulo M′CO) se convierte en una longitud efectiva. (El signo menos es necesario para que ( φ ′ , λ ′) estén relacionados con la retícula rotada de la misma manera que ( φ , λ ) están relacionados con la retícula estándar). Los ejes cartesianos ( x ′, y ′ ) están relacionados con la retícula rotada de la misma manera que los ejes ( x , y ) están relacionados con la retícula estándar.
La proyección de Mercator de tangente transversal define las coordenadas ( x ′ , y ′ ) en términos de - λ ′ y φ ′ por las fórmulas de transformación de la proyección de Mercator Normal tangente:
![{\ displaystyle x '= - a \ lambda' \, \ qquad y '= {\ frac {a} {2}} \ ln \ left [{\ frac {1+ \ sin \ varphi'} {1- \ sin \ varphi '}} \ right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ec29e50c7aa771e9e79688ca1207e26663b4e2e)
Esta transformación proyecta el meridiano central a una línea recta de longitud finita y, al mismo tiempo, proyecta los círculos grandes a través de E y W (que incluyen el ecuador) a infinitas líneas rectas perpendiculares al meridiano central. Los paralelos y meridianos verdaderos (distintos del ecuador y el meridiano central) no tienen una relación simple con la retícula rotada y se proyectan en curvas complicadas.
La relación entre las retículas [ editar ]
Los ángulos de las dos retículas se relacionan mediante el uso de trigonometría esférica en el triángulo esférico NM′P definido por el meridiano verdadero a través del origen, OM′N, el meridiano verdadero a través de un punto arbitrario, MPN y el gran círculo WM′PE. Los resultados son: [26]
Fórmulas de transformación directa [ editar ]
Las fórmulas directas que dan las coordenadas cartesianas ( x , y ) siguen inmediatamente de lo anterior. Configurando x = y ′ e y = - x ′ (y restaurando los factores de k 0 para acomodar las versiones secantes)
![{\ displaystyle {\ begin {alineado} x (\ lambda, \ varphi) & = {\ frac {1} {2}} k_ {0} a \ ln \ left [{\ frac {1+ \ sin \ lambda \ cos \ varphi} {1- \ sin \ lambda \ cos \ varphi}} \ right], \\ [5px] y (\ lambda, \ varphi) & = k_ {0} a \ arctan \ left [\ sec \ lambda \ tan \ varphi \ right], \ end {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6980ee67020617f53a986c6eeb5d7af266381d9)
Las expresiones anteriores se dan en Lambert [1] y también (sin derivaciones) en Snyder, [13] Maling [27] y Osborne [26] (con todos los detalles).
Fórmulas de transformación inversa [ editar ]
Invirtiendo las ecuaciones anteriores da
![{\ displaystyle {\ begin {alineado} \ lambda (x, y) & = \ arctan \ left [\ sinh {\ frac {x} {k_ {0} a}} \ sec {\ frac {y} {k_ { 0} a}} \ right], \\ [5px] \ varphi (x, y) & = \ arcsin \ left [{\ mbox {sech}} \; {\ frac {x} {k_ {0} a} } \ sin {\ frac {y} {k_ {0} a}} \ right]. \ end {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d79354a0dad109450479ec16db488ad896d6d810)
Escala de puntos [ editar ]
En términos de las coordenadas con respecto a la retícula rotada, el factor de escala del punto viene dado por k = sec φ ′ : esto puede expresarse en términos de las coordenadas geográficas o en términos de las coordenadas de proyección:
![{\ displaystyle {\ begin {alineado} k (\ lambda, \ varphi) & = {\ frac {k_ {0}} {\ sqrt {1- \ sin ^ {2} \ lambda \ cos ^ {2} \ varphi }}}, \\ [5px] k (x, y) & = k_ {0} \ cosh \ left ({\ frac {x} {k_ {0} a}} \ right). \ End {alineado}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f258c8b8bf11cd3f37adf8a4d2372b9c9ea58b5a)
La segunda expresión muestra que el factor de escala es simplemente una función de la distancia desde el meridiano central de la proyección. Un valor típico del factor de escala es k 0 = 0.9996, de modo que k = 1 cuando x es aproximadamente 180 km. Cuando x es de aproximadamente 255 km yk 0 = 1.0004: el factor de escala está dentro del 0.04% de la unidad en una franja de aproximadamente 510 km de ancho.
Convergencia [ editar ]
El ángulo de convergencia γ en un punto de la proyección se define por el ángulo medido desde el meridiano proyectado, que define el norte verdadero, hasta una línea de la constante de la cuadrícula x , que define el norte de la cuadrícula. Por lo tanto, γ es positivo en el cuadrante al norte del ecuador y al este del meridiano central y también en el cuadrante al sur del ecuador y al oeste del meridiano central. La convergencia debe agregarse a una marcación de cuadrícula para obtener una marcación del norte verdadero. Para el secante Mercator transversal, la convergencia se puede expresar [26] en términos de coordenadas geográficas o en términos de coordenadas de proyección:
![{\ displaystyle {\ begin {alineado} \ gamma (\ lambda, \ varphi) & = \ arctan (\ tan \ lambda \ sin \ varphi), \\ [5px] \ gamma (x, y) & = \ arctan \ izquierda (\ tanh {\ frac {x} {k_ {0} a}} \ tan {\ frac {y} {k_ {0} a}} \ derecha). \ end {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4770e247d333c3a92fb819ff8d133cd20555aca0)
No hay comentarios:
Publicar un comentario