El uso de la proyección ortográfica en la cartografía se remonta a la antigüedad. Al igual que la proyección estereográfica y la proyección gnomónica , la proyección ortográfica es una proyección en perspectiva (o azimutal) , en la que la esfera se proyecta sobre un plano tangente o plano secante . El punto de perspectiva para la proyección ortográfica está a una distancia infinita . Representa un hemisferio del globo tal como aparece desde el espacio exterior , donde el horizonte es un gran círculo.. Las formas y áreas están distorsionadas , particularmente cerca de los bordes.
Historia [ editar ]
La proyección ortográfica se conoce desde la antigüedad, y sus usos cartográficos están bien documentados. Hiparco usó la proyección en el siglo II a. C. para determinar los lugares de ascenso de estrellas y de estrellas. Alrededor del 14 aC, el ingeniero romano Marcus Vitruvius Pollio utilizó la proyección para construir relojes de sol y para calcular las posiciones del sol. [2]
Vitruvio también parece haber ideado el término ortográfico (del griego orthos (= "straight") y graphē (= "drawing")) para la proyección. Sin embargo, el nombre analemma , que también significa un reloj de sol con latitud y longitud, fue el nombre común hasta que François d'Aguilon de Amberes promovió su nombre actual en 1613. [2]
Los primeros mapas supervivientes de la proyección aparecen como dibujos en madera de globos terrestres de 1509 (anónimo), 1533 y 1551 (Johannes Schöner), y 1524 y 1551 (Apian). Estos eran crudos. Un mapa altamente refinado, diseñado por el agente del Renacimiento Albrecht Dürer y ejecutado por Johannes Stabius,apareció en 1515. [2]
Las fotografías de la Tierra y otros planetas de naves espaciales han inspirado un renovado interés en la proyección ortográfica en astronomía y ciencia planetaria .
Matemáticas [ editar ]
Las fórmulas para la proyección ortográfica esférica se derivan utilizando trigonometría . Están escritos en términos de longitud ( λ ) y latitud ( φ ) en la esfera . Defina el radio de la esfera R y el punto central (y el origen ) de la proyección ( λ 0 , φ 0 ). Las ecuaciones para la proyección ortográfica en el plano tangente ( x , y ) se reducen a lo siguiente: [1]
Las latitudes más allá del rango del mapa deben recortarse calculando la distancia c desde el centro de la proyección ortográfica. Esto asegura que los puntos en el hemisferio opuesto no sean trazados:
- .
El punto debe recortarse del mapa si cos ( c ) es negativo.
Las fórmulas inversas están dadas por:
dónde
Para el cálculo de las fórmulas inversas (p. Ej., Utilizando C / C ++ , Fortran u otro lenguaje de programación ), se recomienda el uso de la forma atan2 de dos argumentos de la función tangente inversa (a diferencia de atan ). Esto asegura que el signo de la proyección ortográfica tal como está escrito sea correcto en todos los cuadrantes.
Las fórmulas inversas son particularmente útiles cuando se intenta proyectar una variable definida en una cuadrícula ( λ , φ ) en una cuadrícula rectilínea en ( x , y ). La aplicación directa de la proyección ortográfica produce puntos dispersos en ( x , y ), lo que crea problemas para el trazado y la integración numérica . Una solución es comenzar desde el plano de proyección ( x , y ) y construir la imagen a partir de los valores definidos en ( λ , φ ) utilizando las fórmulas inversas de la proyección ortográfica.
Ver Referencias para una versión elipsoidal de la proyección del mapa ortográfico. [3]
Proyecciones ortográficas sobre cilindros [ editar ]
En un sentido amplio, todas las proyecciones con el punto de perspectiva en el infinito (y, por lo tanto, líneas de proyección paralelas) se consideran ortográficas, independientemente de la superficie sobre la que se proyecten. Este tipo de proyecciones distorsionan los ángulos y las áreas cercanas a los polos. [ aclaración necesaria ]
Un ejemplo de una proyección ortográfica sobre un cilindro es la proyección cilíndrica de igual área de Lambert .
La proyección quincuncial de Peirce [1] es una proyección de mapa conformal desarrollada por Charles Sanders Peirceen 1879. La proyección tiene la propiedad distintiva de que se puede colocar en mosaico hasta el infinito en el plano, con cruces de bordes completamente lisos, excepto cuatro puntos singulares por azulejo. La proyección se ha visto en la fotografía digital para retratar vistas de 360 °. La descripción quincuncial se refiere a la disposición de cuatro cuadrantes del globo terráqueo alrededor del hemisferio central en un patrón cuadrado general. Normalmente, la proyección está orientada de tal manera que el polo norte se encuentra en el centro.
Historia [ editar ]
La maduración del análisis complejo condujo a técnicas generales para el mapeo conforme , donde los puntos de una superficie plana se manejan como números en el plano complejo . Mientras trabajaba en el US Coast and Geodetic Survey , el filósofo estadounidense Charles Sanders Peircepublicó su proyección en 1879 (Peirce 1879), [2] se inspiró en la transformación conformal de 1869 de HA Schwarz de un círculo en un polígono de n lados ( conocido como el mapeo de Schwarz-Christoffel). En el aspecto normal, la proyección de Peirce presenta el hemisferio norte en un cuadrado; laEl hemisferio sur está dividido en cuatro triángulos isósceles simétricamente que rodean al primero, similar a las proyecciones en forma de estrella. En efecto, todo el mapa es un cuadrado, inspirando a Peirce a llamar a su proyección quincuncional , después de la disposición de cinco elementos en un quincunce .
Después de que Peirce presentara su proyección, otros dos cartógrafos desarrollaron proyecciones similares del hemisferio (o toda la esfera, después de un reordenamiento adecuado) en un cuadrado: Guyou en 1887 y Adams en 1925. [3] Las tres proyecciones son versiones transversales entre sí. (Ver proyecciones relacionadas abajo).
Descripción formal [ editar ]
La proyección quincuncial de Peirce se "forma transformando la proyección estereográfica con un polo en el infinito, por medio de una función elíptica". [4] El Peirce quincuncial es realmente una proyección del hemisferio, pero sus propiedades de teselación (ver más abajo) permiten su uso para toda la esfera. La proyección mapea el interior de un círculo en el interior de un cuadrado por medio del mapeo Schwarz-Christoffel , de la siguiente manera: [5]
donde sd es la relación de dos funciones elípticas de Jacobi : sn / dn; w es el punto mapeado en el plano como un número complejo ( w = x + iy ); y r es la proyección estereográfica con una escala de 1/2 en el centro. Se puede usar una integral elíptica del primer tipo para resolver w . La notación de coma utilizada para sd (u, k) significa que 1 / √ 2 es el módulo para la relación de función elíptica, en oposición al parámetro [que se escribiría sd (u | m)] o la amplitud[que se escribiría sd (u \ α)]. El mapeo tiene un factor de escala de 1/2 en el centro, como la proyección estereográfica generadora.
Propiedades [ editar ]
Según Peirce, su proyección tiene las siguientes propiedades (Peirce, 1879):
- La esfera se presenta en un cuadrado.
- La parte donde la exageración de la escala equivale a duplicar la del centro es solo el 9% del área de la esfera, contra el 13% para la proyección de Mercator y el 50% para la proyección estereográfica.
- La curvatura de las líneas que representan grandes círculos es, en todos los casos, muy leve, sobre la mayor parte de su longitud.
- Es conforme en todas partes, excepto en las cuatro esquinas del hemisferio interno (por lo tanto, los puntos medios de los bordes de la proyección), donde el ecuador y los cuatro meridianos cambian de dirección bruscamente (el ecuador está representado por un cuadrado). Estas son singularidades donde falla la diferenciabilidad .
- Puede ser teselado en todas las direcciones.
Mapas quincunciales de azulejos de Peirce [ editar ]
La proyección tesela el plano; es decir, las copias repetidas pueden cubrir completamente (mosaico) un área arbitraria, las características de cada copia coinciden exactamente con las de sus vecinos. (Ver el ejemplo a la derecha). Además, los cuatro triángulos del segundo hemisferio de la proyección quincuncial de Peirce se pueden reorganizar como otro cuadrado que se coloca al lado del cuadrado que corresponde al primer hemisferio, lo que resulta en un rectángulo con una relación de aspecto de 2: 1; esta disposición es equivalente al aspecto transversal de la proyección del hemisferio en un cuadrado de Guyou . [6]
Usos conocidos [ editar ]
Como muchas otras proyecciones basadas en números complejos, el quincuncial de Peirce rara vez se ha utilizado con fines geográficos. Uno de los pocos casos registrados es en 1946, cuando fue utilizado por el mapa mundial de rutas aéreas de la Costa y el Estudio Geodésico de los Estados Unidos. [6]Recientemente se ha utilizado para presentar panoramas esféricos con fines prácticos y estéticos, donde puede presentar toda la esfera y la mayoría de las áreas son reconocibles [7]
Proyecciones relacionadas [ editar ]
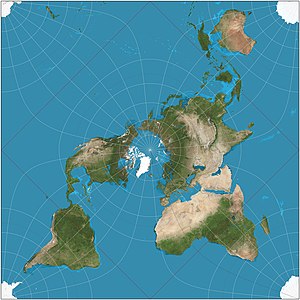
En el aspecto transversal , un hemisferio se convierte en la proyección del hemisferio en un cuadrado de Adams (el polo se coloca en la esquina del cuadrado). Sus cuatro singularidades se encuentran en el Polo Norte, el Polo Sur, en el ecuador a 25 ° W y en el ecuador a 155 ° E, en los océanos Ártico, Atlántico y Pacífico, y en la Antártida. [8] Ese gran círculo divide los hemisferios occidental y oriental tradicionales .
En el aspecto oblicuo (45 grados) de un hemisferio se convierte en la proyección hemisou-en-un-cuadrado de Guyou (el polo se coloca en el centro del borde del cuadrado). Sus cuatro singularidades se encuentran a 45 grados de latitud norte y sur en el gran círculo compuesto por el meridiano 20 ° W y los meridianos 160 ° E, en los océanos Atlántico y Pacífico. [8] Ese gran círculo divide los hemisferios tradicional occidental y oriental.











No hay comentarios:
Publicar un comentario