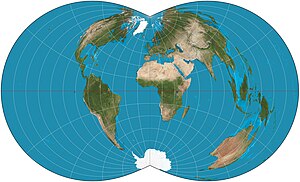
La proyección policónica rectangular es una proyección de mapa que fue mencionada por primera vez en 1853 por el US Coast Survey , donde se desarrolló y se usó para partes de los EE. UU. Que excedían aproximadamente un grado cuadrado. Pertenece a la clase de proyección policónica , que consiste en proyecciones de mapas cuyos paralelos son arcos circulares no concéntricos, excepto el ecuador, que es recto. A veces, el policónico rectangular se denomina proyección de la Oficina de Guerra debido a su uso por parte de la Oficina de Guerra Británica para mapas topográficos. [1] No se usa mucho en estos días, ya que prácticamente todos los sistemas de redes militares se han movido hacia sistemas de proyección conformal, típicamente modelados en laProyección transversal de Mercator.
Descripción [ editar ]
El policónico rectangular tiene una latitud especificable (junto con la latitud del signo opuesto) a lo largo de la cual la escala es correcta. La escala también es cierta en el meridiano central de la proyección. Los meridianos están espaciados de manera tal que se encuentran con los paralelos en ángulos rectos en el aspecto ecuatorial; Este rasgo da cuenta del nombre rectangular .
![{\ displaystyle {\ begin {alineado} x & = \ cot \ varphi \ sin E \\ y & = \ varphi - \ varphi _ {0} + \ left (1- \ cos E \ right) \ cot \ varphi \\ E & = 2 \ arctan \ left (A \ sin \ varphi \ right) \\ A & = \ tan \ left [{\ frac {1} {2}} \ left (\ lambda - \ lambda _ {0} \ right) \ sin \ varphi _ {1} \ right] \ csc \ varphi _ {1} \ end {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38535f7795ca9d5ad37b5e96c56a869929eade45)
dónde:
- λ es la longitud del punto a proyectar;
- φ es la latitud del punto a proyectar;
- λ 0 es la longitud del meridiano central,
- φ 0 es la latitud elegida para ser el origen a lo largo de λ 0 ;
- φ 1 es la latitud cuyo paralelo se elige para tener la escala correcta.
Para evitar la división por cero, las fórmulas anteriores se extienden de modo que si φ = 0, entonces x = λ - λ 0y y = - φ 0 .
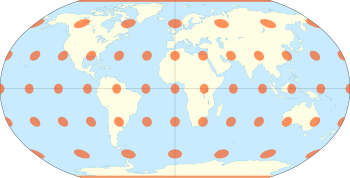
La proyección de Robinson es una proyección cartográfica de un mapa del mundo que muestra el mundo entero a la vez. Fue creado específicamente en un intento de encontrar un buen compromiso con el problema de mostrar fácilmente todo el globo como una imagen plana. [1]
La proyección de Robinson fue diseñada por Arthur H. Robinson en 1963 en respuesta a una apelación de la compañía Rand McNally , que ha utilizado la proyección en mapas mundiales de propósito general desde entonces. Robinson publicó detalles de la construcción de la proyección en 1974. La National Geographic Society (NGS) comenzó a usar la proyección de Robinson para mapas mundiales de propósito general en 1988, en reemplazo de la proyección de Van der Grinten . [2] En 1998, NGS abandonó la proyección de Robinson para ese uso a favor de la proyección de Winkel tripel , ya que esta última "reduce la distorsión de las masas de tierra cuando se acercan a los polos".
Fortalezas y debilidades [ editar ]
La proyección de Robinson no es de área equitativa ni conforme , abandonando ambos por un compromiso. El creador sintió que esto producía una mejor visión general de la que podría lograrse al adherirse a cualquiera de los dos. Los meridianos se curvan suavemente, evitando los extremos, pero estirando los polos en líneas largas en lugar de dejarlos como puntos. [1]
Por lo tanto, la distorsión cerca de los polos es grave, pero disminuye rápidamente a niveles moderados que se alejan de ellos. Los paralelos rectos implican una distorsión angular severa en las latitudes altas hacia los bordes exteriores del mapa, una falla inherente en cualquier proyección pseudocilíndrica. Sin embargo, en el momento en que se desarrolló, la proyección cumplió efectivamente con el objetivo de Rand McNally de producir representaciones atractivas de todo el mundo. [5] [6]
Formulación [ editar ]
| Latitud | X | Y |
|---|---|---|
| 0 ° | 1.0000 | 0.0000 |
| 5 ° | 0.9986 | 0.0620 |
| 10 ° | 0.9954 | 0.1240 |
| 15 | 0.9900 | 0.1860 |
| 20 ° | 0.9822 | 0.2480 |
| 25 ° | 0.9730 | 0.3100 |
| 30 ° | 0.9600 | 0.3720 |
| 35 ° | 0.9427 | 0.4340 |
| 40 ° | 0.9216 | 0.4958 |
| 45 ° | 0.8962 | 0.5571 |
| 50 ° | 0.8679 | 0.6176 |
| 55 ° | 0.8350 | 0.6769 |
| 60 ° | 0.7986 | 0.7346 |
| sesenta y cinco | 0.7597 | 0.7903 |
| 70 ° | 0.7186 | 0.8435 |
| 75 ° | 0.6732 | 0.8936 |
| 80 ° | 0.6213 | 0.9394 |
| 85 ° | 0.5722 | 0.9761 |
| 90 ° | 0.5322 | 1.0000 |
La tabla está indexada por latitud en intervalos de 5 grados; Los valores intermedios se calculan utilizando la interpolación . Robinson no especificó ningún método de interpolación en particular, pero se informa que él mismo usó la interpolación de Aitken . [10] La columna X es la relación de la longitud del paralelo a la longitud del ecuador; la columna Y se puede multiplicar por 0.2536 [11] para obtener la relación de la distancia de ese paralelo desde el ecuador hasta la longitud del ecuador. [7] [9]
donde R es el radio del globo terráqueo en la escala del mapa, λ es la longitud del punto a trazar, y λ 0 es el meridiano central elegido para el mapa (tanto λ como λ 0 se expresan en radianes ).
Las consecuencias simples de estas fórmulas son:
- Con x calculada como un multiplicador constante del meridiano en todo el paralelo, los meridianos de longitud están igualmente espaciados a lo largo del paralelo.
- Dado que y no tiene dependencia en la longitud, los paralelos son líneas horizontales rectas.
La red Schmidt es un método de dibujo manual para la proyección acimutal de áreas iguales de Lambert utilizando papel cuadriculado. Resulta en un hemisferio lateral de la Tierra con la cuadrícula de paralelos y meridianos . El método es común en las ciencias geofísicas.
Construcción [ editar ]
En la figura, la propiedad de preservación de área de la proyección se puede ver comparando un sector de cuadrícula cerca del centro de la red con uno en el extremo derecho de la red. Los dos sectores tienen la misma área en la esfera y la misma área en el disco. La propiedad que distorsiona el ángulo se puede ver al examinar las líneas de la cuadrícula; la mayoría de ellos no se intersecan en ángulos rectos en la red Schmidt. Una sola red de Schmidt solo puede representar un hemisferio de la tierra; normalmente se usa un par de redes Schmidt para representar ambos lados del globo.
Es relativamente sencillo volver a trazar un mapa cuadriculado del mundo en una red Schmidt si se elige el azimut para que sea la unión del ecuador con cualquier meridiano en particular de la cuadrícula del mapa del mundo. Cada cuadrícula que rodea esta longitud elegida se vuelve a trazar en la cuadrícula distorsionada correspondiente en la red de Schmidt. Los puntos de latitud-longitud se pueden trazar en relación con la longitud del acimut, interpolando entre las líneas de la cuadrícula en la red de Schmidt. Para mayor precisión, es útil tener una red con un espaciado más fino que 10 °; Las separaciones de 2 ° son comunes.
La red Schmidt no es una cuadrícula adecuada para representar el hemisferio norte o sur de la Tierra (porque las líneas no corresponderían a meridianos o paralelos en una proyección de este tipo). Sin embargo, se puede usar como un dispositivo de medición escalar para proyectar puntos de latitud-longitud en un círculo en blanco del mismo tamaño, para producir una proyección de áreas iguales de Lambert con el azimut en el polo norte o sur. La intersección de los paralelos con el círculo exterior se puede utilizar como un factotransportador para trazar la longitud de un punto como el ángulo en la proyección polar. El eje horizontal de la red Schmidt se puede utilizar como un dispositivo de medición escalar para convertir la latitud del punto (en relación con el polo) en una distancia radial desde el centro del círculo. Alternativamente, la red Schmidt podría reemplazarse por completo con una cuadrícula polar proyectada correctamente, y los cuadrados de cuadrícula de un mapa re-dibujados en este disco.
Utilizar [ editar ]
Los investigadores en geología estructural utilizan la proyección azimutal Lambert a parcela lineación y foliaciónen rocas, caras de fricción en los fallos , y otras características lineales y planas. En este contexto, la proyección se llama proyección hemisférica de igual área . La red Schmidt se usa a menudo para esbozar la proyección azimutal de Lambert para estos fines. [1] Por el contrario, la red Wulff ("proyección de ángulo igual") se utiliza para trazar ejes y caras cristalográficos .
No hay comentarios:
Publicar un comentario