PROYECCIONES DE MAPAS

proyección loximutal es una proyección de mapa introducida por Karl Siemon en 1935, e independientemente en 1966 por Waldo R. Tobler, quien la llamó. ^[1] Se caracteriza por el hecho de que los loxódromos(líneas de rumbo) de un punto central elegido (la intersección del meridiano central y la latitud central ) se muestran líneas rectas, correctas en acimut desde el centro, y son "verdaderas a escala" en el sentido de que las distancias medidas a lo largo de tales líneas son proporcionales a las longitudes de las líneas de rumbo correspondientes en la superficie de la tierra. No es una proyección de igual área.ni conformal .

Un loxódromo en la superficie de la tierra es una curva de rumbo constante: se encuentra con cada paralelo de latitud en el mismo ángulo. Supongamos que su rumbo es θ al norte del este, por lo que, por ejemplo, al este, es θ  = 0; hacia el norte es θ  = un ángulo recto; al oeste es θ  = un semicírculo. La longitud total del loxódromo a medida que va desde el polo sur al polo norte se ve con bastante frecuencia que es π R  csc  θ donde Res el radio de la tierra (en particular, si el loxódromo va directamente hacia el este, circunda la tierra infinitamente muchas veces sin acercarse a ninguno de los polos, por lo que su longitud es Let. Deje que un loxódromo pase a través del punto cuya longitud y latitud sean ambas 0 ; llame a esto el "punto central". Suponga que uno comienza en el punto central y recorre una cierta distancia en cierta dirección a lo largo de este loxódromo y llega a la ubicación geográfica. Sea f ( p ) el punto en el ( x ,  y ) - plano alcanzado al ir esa misma distancia en esa misma dirección desde el origen (0, 0). Por lo tanto, f ( p ) ∈  R  × [- π R/2 , π R/2 ]. Ese puntof(p) es la imagen depen el mapa. Más de un loxódromo va desde el punto central a p, pero hay uno único más corto: el que no cruza el meridiano de 180 ° en su camino desde el punto central a p. Si se incluyeran loxodromos que cruzan el meridiano de 180 °, se obtendrían infinitas imágenes de toda la Tierra, ocupando toda la franjaR × [-π R/2 , π R/2 ]. Usando solo el loxódromo más corto único desde el punto central hasta cada puntop Solo da una copia, ocupando una especie de óvalo.

Proyección loximutal del mundo, punto central = 0 ° E, 30 ° N. 15 ° gratícula.

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Proyección de Mercator del mundo entre 82 ° S y 82 ° N.

La proyección de Mercator con la indicatriz de deformación de Tissot .

Mapa del mundo de Mercator 1569 ( Nova et Aucta Orbis Terrae Descriptio ad Usum Navigantium Emendate Accommodation ) que muestra las latitudes 66 ° S a 80 ° N.

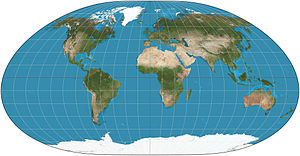
La proyección de Mercator es una proyección de mapa cilíndrica presentada por el geógrafo y cartógrafo flamenco Gerardus Mercator en 1569. Se convirtió en la proyección de mapa estándar para la navegación náutica debido a su capacidad para representar líneas de curso constante , conocidas como líneas de rumbo o loxodromes, como segmentos rectos. Que conserven los ángulos con los meridianos. Aunque la escala lineal es igual en todas las direcciones alrededor de cualquier punto, preservando así los ángulos y las formas de los objetos pequeños (haciéndolo una proyección de mapa conforme)), la proyección de Mercator distorsiona el tamaño de los objetos a medida que la latitud aumenta desde el ecuador hasta los polos, donde la escala se vuelve infinita. Así, por ejemplo, las masas de tierra como Groenlandia y la Antártidaparecen mucho más grandes de lo que realmente son, en relación con las masas de tierra cercanas al ecuador, como África Central.

Propiedades y detalles históricos [ editar ]

La edición 1569 de Mercator era un gran planisferio que medía 202 por 124 cm (80 por 49 pulgadas), impreso en dieciocho hojas separadas. Como en todas las proyecciones cilíndricas , los paralelos y los meridianos son rectos y perpendiculares entre sí. Para lograr esto, el inevitable estiramiento este-oeste del mapa, que aumenta a medida que aumenta la distancia del ecuador , se acompaña en la proyección de Mercator con un correspondiente estiramiento norte-sur, de modo que en cada punto la escala este-oeste es lo mismo que la escala norte-sur, lo que la hace una proyección de mapa conforme . Las proyecciones conformes conservan los ángulos alrededor de todas las ubicaciones.

Debido a que la escala lineal de un mapa de Mercator aumenta con la latitud, distorsiona el tamaño de los objetos geográficos lejos del ecuador y transmite una percepción distorsionada de la geometría global del planeta. En latitudes superiores a 70 ° norte o sur, la proyección de Mercator es prácticamente inutilizable, porque la escala lineal se vuelve infinitamente grande en los polos. Por lo tanto, un mapa de Mercator nunca puede mostrar completamente las áreas polares (siempre que la proyección se base en un cilindro centrado en el eje de rotación de la Tierra; consulte la proyección de Mercator transversal para otra aplicación).

Todas las líneas de rumbo constante ( rumbas o loxodromes, aquellas que forman ángulos constantes con los meridianos) están representadas por segmentos rectos en un mapa de Mercator. Las dos propiedades, conformidad y líneas rectas del rumbo, hacen que esta proyección sea especialmente adecuada para la navegación marítima : los cursos y los cojinetes se miden utilizando rosas de viento o transportadores, y las direcciones correspondientes se transfieren fácilmente de un punto a otro, en el mapa, con la ayuda de una regla paralela (por ejemplo).

El nombre y las explicaciones dadas por Mercator a su mapa del mundo ( Nova et Aucta Orbis Terrae Descriptio ad Usum Navigantium Emendata : "descripción nueva y aumentada de la Tierra corregida para uso de marineros") muestran que fue concebida expresamente para el uso de navegación marina . Aunque el método de construcción no está explicado por el autor, Mercator probablemente utilizó un método gráfico, transfiriendo algunas líneas de trazos previamente trazadas en un globo a una cuadrícula cuadrada (cuadrícula formada por líneas de latitud y longitud), y luego ajustando el espaciado entre los paralelos de modo que esas líneas se volvieron rectas, formando el mismo ángulo con los meridianos que en el globo.

El desarrollo de la proyección de Mercator representó un gran avance en la cartografía náutica del siglo XVI. Sin embargo, estaba muy adelantado a su tiempo, ya que las antiguas técnicas de navegación y topografía no eran compatibles con su uso en la navegación. Dos problemas principales impidieron su aplicación inmediata: la imposibilidad de determinar la longitud en el mar con la precisión adecuada y el hecho de que las direcciones magnéticas, en lugar de las direcciones geográficas , se utilizaron en la navegación. Solo a mediados del siglo XVIII, después de que se inventó el cronómetro marino y se conoció la distribución espacial de la declinación magnética , los navegadores pudieron adoptar la proyección de Mercator por completo.

Varios autores están asociados con el desarrollo de la proyección de Mercator:

• El alemán Erhard Etzlaub (c. 1460-1532), que había grabado "mapas de brújula" en miniatura (aproximadamente 10 × 8 cm) de Europa y partes de África, latitudes 67 ° –0 °, para permitir el ajuste de sus relojes de sol portátiles de bolsillo. , durante décadas se declaró que había diseñado "una proyección idéntica a la de Mercator".
• El matemático y cosmógrafo portugués Pedro Nunes (1502–1578), quien describió por primera vez el loxódromo y su uso en la navegación marina, y sugirió la construcción de un atlas náutico compuesto de varias hojas a gran escala en la proyección equidistante cilíndrica como una forma de minimizar la distorsión de direcciones. Si estas hojas se llevaran a la misma escala y se armaran, se obtendría una aproximación de la proyección de Mercator (1537).
• El matemático inglés Edward Wright (c. 1558–1615), quien publicó tablas precisas para su construcción (1599, 1610).
• Los matemáticos ingleses Thomas Harriot (1560–1621) y Henry Bond (c.1600–1678) que, independientemente (c.1600 y 1645), asociaron la proyección de Mercator con su fórmula logarítmica moderna, que luego se deduce por cálculo.

Usos [ editar ]

La proyección de Mercator muestra a Groenlandia como más grande que Australia; en realidad, Australia es más de tres veces y media más grande que Groenlandia.

Como en todas las proyecciones de mapas , las formas o los tamaños son distorsiones del verdadero diseño de la superficie de la Tierra. La proyección de Mercator exagera áreas alejadas del ecuador . Por ejemplo:

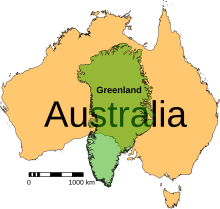
• Groenlandia parece más grande que África , cuando en realidad el área de África es 14 veces mayor y la de Groenlandia es comparable a la de Argelia . África también parece tener aproximadamente el mismo tamaño que Europa , cuando en realidad África es casi 3 veces más grande.
• Alaska tiene tanta área en el mapa como Brasil , cuando el área de Brasil es casi cinco veces mayor que la de Alaska.
• Finlandia aparece con una mayor extensión norte-sur que India , aunque la de India es mayor.
• La Antártida aparece como el continente más grande (y sería infinitamente grande en un mapa completo), aunque en realidad es el quinto en el área.

Una relación entre la proyección de Mercator y el tamaño real de cada país.

La proyección de Mercator todavía se usa comúnmente para la navegación. Por otro lado, debido a las grandes distorsiones del área terrestre, no es adecuado para los mapas mundiales generales. Por lo tanto, el propio Mercator usó la proyección sinusoidal de áreas iguales para mostrar áreas relativas. Sin embargo, a pesar de estas distorsiones, la proyección de Mercator fue, especialmente a finales del siglo XIX y principios del XX, quizás la proyección más común utilizada en los mapas mundiales, a pesar de ser muy criticada por este uso. ^{[1] [2] [3] [4]}Debido a su uso muy común, se supone que influyó en la visión que las personas tienen del mundo, ^[5]y debido a que muestra a los países cercanos al Ecuador como demasiado pequeños en comparación con los de Europa y América del Norte, se supone que debe hacer que las personas consideren a esos países como menos importantes. ^[6] Como resultado de estas críticas, la mayoría de los atlas modernos ya no usan la proyección de Mercator para mapas del mundo o para áreas alejadas del ecuador, prefiriendo otras proyecciones cilíndricas o formas de proyección de áreas iguales . Sin embargo, la proyección de Mercator todavía se usa comúnmente en áreas cercanas al ecuador, donde la distorsión es mínima.

Arno Peters provocó controversia cuando propuso lo que ahora se denomina usualmente Proyección de Peterscomo la alternativa a la de Mercator. La proyección que promovió es una parametrización específica de la proyección cilíndrica de áreas iguales . En respuesta, una resolución de 1989 por siete grupos geográficos de América del Norte dejó de lado el uso de proyecciones cilíndricas para mapas mundiales de propósito general, que incluirían tanto el Mercator como el Gall-Peters. ^[7]

Web Mercator [ editar ]

Artículo principal: Web Mercator

Muchos de los principales servicios de mapas de calles en línea ( Bing Maps , OpenStreetMap , Google Maps , MapQuest , Yahoo! Maps y otros) utilizan una variante de la proyección de Mercator para sus imágenes de mapa ^[8] llamada Web Mercator o Google Web Mercator. A pesar de su obvia variación de escala a pequeña escala, la proyección se adapta bien como un mapa del mundo interactivo que se puede ampliar sin problemas a mapas de gran escala (locales), donde existe una distorsión relativamente pequeña debido a la casi conformidad de la variante de proyección .

Los principales sistemas de mosaico de servicios de cartografía de calles en línea muestran la mayor parte del mundo en el nivel de zoom más bajo como una sola imagen cuadrada, excluyendo las regiones polares mediante el truncamiento en latitudes de φ _máx  = ± 85.05113 °. (Consulte a continuación .) Los valores de latitud fuera de este rango se asignan utilizando una relación diferente que no divergen en  φ  = ± 90 °. ^{[ cita requerida ]}

Matemáticas de la proyección de Mercator [ editar ]

El modelo esférico [ editar ]

Aunque la superficie de la Tierra está mejor modelada por un elipsoide de revolución oblato , para mapas a pequeña escala , el elipsoide es aproximado por una esfera de radio a . Existen muchos métodos diferentes para calcular a . Las más simples incluyen (a) el radio ecuatorial del elipsoide, (b) la media aritmética o geométrica de los semiejes del elipsoide, (c) el radio de la esfera que tiene el mismo volumen que el elipsoide. ^[9]El rango de todas las opciones posibles es de aproximadamente 35 km, pero para las aplicaciones a pequeña escala (región grande) la variación puede ignorarse, y se pueden tomar valores medios de 6,371 km y 40,030 km para el radio y la circunferencia, respectivamente. Estos son los valores utilizados para ejemplos numéricos en secciones posteriores. Solo la cartografía de alta precisión en mapas a gran escala requiere un modelo elipsoidal.

Proyecciones cilíndricas [ editar ]

La aproximación esférica de la Tierra con radio a puede ser modelada por una esfera más pequeña de radio R , llamada el globo en esta sección. El globo determina la escala del mapa. Las diversas proyecciones cilíndricasespecifican cómo se transfiere el detalle geográfico del globo a un cilindro tangencial hacia él en el ecuador. El cilindro se desenrolla para dar el mapa plano. ^[10] [11] La fracción R/a se llama fracción representativa (RF) o escala principalde la proyección. Por ejemplo, un mapa de Mercator impreso en un libro puede tener un ancho ecuatorial de 13,4 cm correspondiente a un radio de globo de 2,13 cm y una RF de aproximadamente 1/300M (M se usa como una abreviatura de 1,000,000 al escribir una RF), mientras que Mercator El mapa original de 1569 tiene un ancho de 198 cm correspondiente a un radio de globo de 31,5 cm y una RF de aproximadamente 1/20M .

Una proyección de mapa cilíndrica se especifica mediante fórmulas que vinculan las coordenadas geográficas de latitud  φ y longitud  λ a coordenadas cartesianas en el mapa con el origen en el ecuador y el eje x a lo largo del ecuador. Por construcción, todos los puntos en el mismo meridiano se encuentran en el mismo generador ^[12] del cilindro a un valor constante de x , pero la distancia y a lo largo del generador (medida desde el ecuador) es una función arbitraria ^[13] de latitud, y ( φ). En general, esta función no describe la proyección geométrica (como los rayos de luz sobre una pantalla) desde el centro del globo hasta el cilindro, que es solo una de las muchas formas ilimitadas de proyectar conceptualmente un mapa cilíndrico.

Dado que el cilindro es tangencial al globo en el ecuador, el factor de escala entre el globo y el cilindro es la unidad en el ecuador, pero en ninguna otra parte. En particular, dado que el radio de un paralelo, o círculo de latitud, es R  cos  φ , el paralelo correspondiente en el mapa debe haberse estirado por un factor de 1/cos φ = sec φ. Este factor de escala en el paralelo se denota convencionalmente por k y el factor de escala correspondiente en el meridiano se denota por  h . ^[14]

Geometría de elementos pequeños [ editar ]

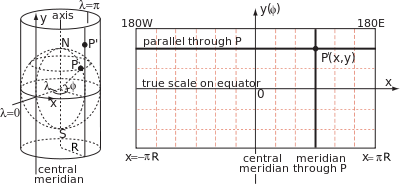
Las relaciones entre y ( φ ) y las propiedades de la proyección, tales como la transformación de los ángulos y la variación de la escala, se siguen de la geometría de los correspondientes pequeños elementos en el globo y el mapa. La siguiente figura muestra un punto P en la latitud  φ y la longitud  λ en el globo terráqueo y un punto cercano Q en la latitud φ  +  δφ y la longitud λ  +  δλ . Las líneas verticales PK y MQ son arcos de meridianos de longitud Rδφ . ^[15] Las líneas horizontales PM y KQ son arcos paralelos de longitud R (cos  φ ) δλ. ^[16] Los puntos correspondientes en la proyección definen un rectángulo de ancho  δx y altura  δy .

Para elementos pequeños, el ángulo PKQ es aproximadamente un ángulo recto y, por lo tanto,

$${\ displaystyle \ tan \ alpha \ approx {\ frac {R \ cos \ varphi \, \ delta \ lambda} {R \, \ delta \ varphi}}, \ qquad \ qquad \ tan \ beta = {\ frac {\ delta x} {\ delta y}},}

Los factores de escala mencionados anteriormente de globo a cilindro están dados por

factor de escala paralela     $${\ displaystyle \ quad k (\ varphi) \; = \; {\ frac {P'M '} {PM}} \; = \; {\ frac {\ delta x} {R \ cos \ varphi \, \ delta \ lambda}},}

factor de escala meridiana   $${\ displaystyle \ quad h (\ varphi) \; = \; {\ frac {P'K '} {PK}} \; = \ frac {\ delta y} {R \ delta \ varphi \,} }.}

Dado que los meridianos están asignados a líneas de constante x , debemos tener x = R ( λ - λ ₀ ) y δx  =  Rδλ , ( λ en radianes). Por lo tanto, en el límite de elementos infinitesimalmente pequeños

$${\ displaystyle \ tan \ beta = {\ frac {R \ sec \ varphi} {y '(\ varphi)}} \ tan \ alpha \ ,, \ qquad k = \ sec \ varphi \ ,, \ qquad h = { \ frac {y '(\ varphi)} {R}}.}

Derivación de la proyección de Mercator [ editar ]

La elección de la función y ( φ ) para la proyección de Mercator está determinada por la demanda de que la proyección sea conforme, una condición que se puede definir de dos maneras equivalentes:

• Igualdad de ángulos . La condición de que un curso de navegación de azimut α constante en el mundo se asigne a una cuadrícula constante con β en el mapa. El ajuste de α  =  β en las ecuaciones anteriores da y ′ ( φ ) =  R  sec  φ .
• Isotropía de factores de escala . Esta es la afirmación de que el factor de escala del punto es independiente de la dirección, de modo que la proyección conserva las pequeñas formas. Configuración h =  k en las ecuaciones anteriores de nuevo da y ' ( φ ) =  R  sec  φ .

Integrando la ecuación

$${\ displaystyle y '(\ varphi) = R \ sec \ varphi,}

con y (0) = 0, utilizando tablas integrales ^[17] o métodos elementales , ^[18] da y (y). Por lo tanto,

$${\ displaystyle x = R (\ lambda - \ lambda _ {0}), \ qquad y = R \ ln \ left [\ tan \ left ({\ frac {\ pi} {4}} + {\ frac {\ varphi} {2}} \ right) \ right].}

En la primera ecuación, λ ₀ es la longitud de un meridiano central arbitrario generalmente, pero no siempre, la de Greenwich (es decir, cero). La diferencia ( λ  -  λ ₀) está en radianes.

La función y ( φ ) se representa junto a φ para el caso R  = 1: tiende a infinito en los polos. Los valores del eje Y lineales generalmente no se muestran en los mapas impresos; en cambio, algunos mapas muestran la escala no lineal de los valores de latitud a la derecha. La mayoría de las veces, los mapas muestran solo una cuadrícula de meridianos y paralelos seleccionados

Transformaciones inversas [ editar ]

$${\ displaystyle \ lambda = \ lambda _ {0} + {\ frac {x} {R}}, \ qquad \ varphi = 2 \ tan ^ {- 1} \ left [\ exp \ left ({\ frac {y } {R}} \ derecha) \ derecha] - {\ frac {\ pi} {2}} \ ,.}

La expresión a la derecha de la segunda ecuación define la función gudermanniana ; es decir, φ  = gd ( y/R ): la ecuación directa se puede escribir como y  =  R · gd ⁻¹ ( φ ). ^[17]

Expresiones alternativas [ editar ]

Hay muchas expresiones alternativas para y ( φ ), todos ellos obtenidos mediante manipulaciones elementales. ^[18]

{\ displaystyle {\ begin {alineado} y & = & {& frac {R} {2}} \ ln \ left [{\ frac {1+ \ sin \ varphi} {1- \ sin \ varphi}} \ right] & = & {R} \ ln \ left [{\ frac {1+ \ sin \ varphi} {\ cos \ varphi}} \ right] & = R \ ln \ left (\ sec \ varphi + \ tan \ varphi \ derecha) \\ [2ex] & = & R \ tanh ^ {- 1} \ left (\ sin \ varphi \ right) & = & R \ sinh ^ {- 1} \ left (\ tan \ varphi \ right) & = R \ operatorname {sgn} (\ varphi) \ cosh ^ {- 1} \ left (\ sec \ varphi \ right) = R \ operatorname {gd} ^ {- 1} (\ varphi). \ end {alineado}}}

Los inversos correspondientes son:

$${\ displaystyle \ varphi = \ sin ^ {- 1} \ left (\ tanh {\ frac {y} {R}} \ right) = \ tan ^ {- 1} \ left (\ sinh {\ frac {y} {R}} \ right) = \ operatorname {sgn} (y) \ sec ^ {- 1} \ left (\ cosh {\ frac {y} {R}} \ right) = \ operatorname {gd} {\ frac {y} {R}}.}

Para ángulos expresados ​​en grados:

$${\ displaystyle x = {\ frac {\ pi R (\ lambda ^ {\ circ} - \ lambda _ {0} ^ {\ circ})} {180}}, \ qquad \ quad y = R \ ln \ left [\ tan \ left (45 + {\ frac {\ varphi ^ {\ circ}} {2}} \ right) \ right].}

Las fórmulas anteriores se escriben en términos del radio globo R . A menudo es conveniente para trabajar directamente con el mapa anchura W  = 2 π R . Por ejemplo, las ecuaciones de transformación básicas se convierten en

$${\ displaystyle x = {\ frac {W} {2 \ pi}} \ left (\ lambda - \ lambda _ {0} \ right), \ qquad \ quad y = {\ frac {W} {2 \ pi} } \ ln \ left [\ tan \ left ({\ frac {\ pi} {4}} + {\ frac {\ varphi} {2}} \ right) \ right].}

Truncamiento y relación de aspecto [ editar ]

La ordenada y de la proyección de Mercator se vuelve infinita en los polos y el mapa debe truncarse en una latitud inferior a noventa grados. Esto no necesita hacerse simétricamente. El mapa original de Mercator se trunca a 80 ° N y 66 ° S con el resultado de que los países europeos se movieron hacia el centro del mapa. La relación de aspecto de su mapa es 198/120 = 1,65. Incluso se han utilizado truncamientos más extremos: un atlas escolar finlandés se truncó a aproximadamente 76 ° N y 56 ° S, una relación de aspecto de 1,97.

La mayoría de los mapas basados ​​en la web utilizan una versión ampliable de la proyección de Mercator con una relación de aspecto de unidad. En este caso, la latitud máxima obtenida debe corresponder a y  = ± W/2 , o equivalentemente y/R  =  π . Cualquiera de las fórmulas de transformación inversa se puede usar para calcular las latitudes correspondientes:

$${\ displaystyle \ varphi = \ tan ^ {- 1} \ left [\ sinh \ left ({\ frac {y} {R}} \ rightarrow) = right] = \ tan ^ {- 1} \ left [\ sinh \ pi \ right] = \ tan ^ {- 1} \ left [11.5487 \ right] = 85.05113 ^ {\ circ}.}

Factor de escala [ editar ]

La figura que compara los elementos infinitesimales en el globo terráqueo y la proyección muestra que cuando α = β, los triángulos PQM y P′Q′M ′ son similares, de modo que el factor de escala en una dirección arbitraria es el mismo que el factor de escala paralelo y meridiano:

$${\ displaystyle {\ frac {\ delta s '} {\ delta s}} = {\ frac {P'Q'} {PQ}} = {\ frac {P'M '} {PM}} = k = { \ frac {P'K '} {PK}} = h = \ sec \ varphi.}

Este resultado es válido para una dirección arbitraria: la definición de isotropía del factor de escala de puntos. La gráfica muestra la variación del factor de escala con la latitud. Algunos valores numéricos se enumeran a continuación.

en la latitud 30 ° el factor de escala es   k  = s 30 ° = 1.15,

en la latitud 45 ° el factor de escala es   k  = seg 45 ° = 1.41,

en la latitud 60 ° el factor de escala es   k  = seg 60 ° = 2,

en la latitud 80 ° el factor de escala es   k  = seg 80 ° = 5.76,

en la latitud 85 ° el factor de escala es   k  = seg 85 ° = 11.5

Trabajar desde el mapa proyectado requiere el factor de escala en términos de la ordenada de Mercator y (a menos que el mapa tenga una escala de latitud explícita). Como las medidas de la regla pueden proporcionar la ordenada del mapa y el ancho W del mapa, entonces y/R  = 2 π y/W y el factor de escala se determina utilizando una de las formas alternativas para las formas de la transformación inversa:

$${\ displaystyle k = \ sec \ varphi = \ cosh \ left ({\ frac {y} {R}} \ right) = \ cosh \ left ({\ frac {2 \ pi y} {W}} \ right) .}

La variación con la latitud a veces se indica mediante múltiples escalas de barra como se muestra a continuación y, por ejemplo, en un atlas escolar finlandés . La interpretación de tales escalas de barra no es trivial. Vea la discusión sobre fórmulas de distancia a continuación.

Escala de área [ editar ]

El factor de escala del área es el producto de las escalas paralela y meridiana hk = sec ² φ . Para Groenlandia, tomando 73 ° como latitud media, hk = 11.7. Para Australia, tomando 25 ° como latitud media, hk = 1.2. Para Gran Bretaña, tomando 55 ° como latitud media, hk = 3.04.

Distorsión [ editar ]

Indicatrices de Tissot sobre la proyección de Mercator.

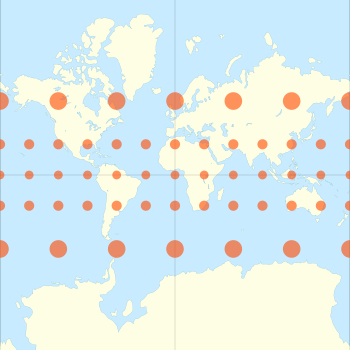
La forma clásica de mostrar la distorsión inherente a una proyección es usar la indicatriz de Tissot . Nicolas Tissot observó que los factores de escala en un punto en una proyección de mapa, especificado por el número h y k , definen una elipse en ese punto. Para proyecciones cilíndricas, los ejes de la elipse se alinean con los meridianos y paralelos. ^{[14] [19] [20]} Para la proyección de Mercator, h  =  k , por lo que las elipses degeneran en círculos con un radio proporcional al valor del factor de escala para esa latitud. Estos círculos se representan en el mapa proyectado con una variación extrema en el tamaño, indicativo de las variaciones de escala de Mercator.

Precisión [ editar ]

Una medida de la precisión de un mapa es una comparación de la longitud de los elementos de línea correspondientes en el mapa y el globo terráqueo. Por lo tanto, por construcción, la proyección de Mercator es perfectamente precisa, k  = 1, a lo largo del ecuador y en ninguna otra parte. En una latitud de ± 25 °, el valor de sec  φ es aproximadamente 1.1 y, por lo tanto, la proyección puede considerarse precisa dentro del 10% en una franja de ancho de 50 ° centrada en el ecuador. Las tiras más estrechas son mejores: sec 8 ° = 1.01, por lo que una tira de ancho 16 ° (centrada en el ecuador) tiene una precisión de 1% o 1 parte en 100. De manera similar, sec 2.56 ° = 1.001, así que una tira de ancho 5.12 ° (centrado en el ecuador) tiene una precisión de 0,1% o 1 parte en 1,000. Por lo tanto, la proyección de Mercator es adecuada para mapear países cercanos al ecuador.

Secante proyección [ editar ]

En una secante (en el sentido de corte) proyección de Mercator del globo se proyecta a un cilindro que corta la esfera en dos paralelos con latitudes ± φ ₁ . La escala ahora es verdadera en estas latitudes, mientras que los paralelos entre estas latitudes se contraen con la proyección y su factor de escala debe ser menor que uno. El resultado es que la desviación de la escala de la unidad se reduce en un rango más amplio de latitudes.

Un ejemplo de tal proyección es

$${\ displaystyle x = 0.99R \ lambda \ qquad y = 0.99R \ ln \ tan \! \ left ({\ frac {\ pi} {4}} + {\ frac {\ varphi} {2}} \ right) \ qquad k \; = 0.99 \ sec \ varphi.}

La escala en el ecuador es 0,99; la escala es k  = 1 en una latitud de aproximadamente ± 8 ° (el valor de φ ₁ ); la escala es k  = 1.01 a una latitud de aproximadamente ± 11.4 °. Por lo tanto, la proyección tiene una precisión del 1%, sobre una franja más ancha de 22 ° en comparación con los 16 ° de la proyección normal (tangente). Esta es una técnica estándar para extender la región sobre la cual una proyección de mapa tiene una precisión dada.

Generalización al elipsoide [ editar ]

Cuando la Tierra está modelada por un esferoide ( elipsoide de revolución), la proyección de Mercator debe modificarse para que siga siendo conforme . Las ecuaciones de transformación y el factor de escala para la versión no secante son ^[21]

{\ displaystyle {\ begin {alineado} x & = R \ left (\ lambda - \ lambda _ {0} \ right), \\ y & = R \ ln \ left [\ tan \ left ({\ frac {\ pi} {4}} + {\ frac {\ varphi} {2}} \ right) \ left ({\ frac {1-e \ sin \ varphi} {1 + e \ sin \ varphi}} \ right) ^ {\ frac {e} {2}} \ right], \\ k & = \ sec \ varphi {\ sqrt {1-e ^ {2} \ sin ^ {2} \ varphi}}. \ end {alineado}}}

El factor de escala es la unidad en el ecuador, como debe ser, ya que el cilindro es tangencial al elipsoide en el ecuador. La corrección elipsoidal del factor de escala aumenta con la latitud, pero nunca es mayor que e ² , una corrección de menos del 1%. (El valor de e ² es aproximadamente 0.006 para todos los elipsoides de referencia). Esto es mucho más pequeño que la imprecisión de la escala, excepto muy cerca del ecuador. Solo las proyecciones precisas de Mercator de las regiones cercanas al ecuador necesitarán las correcciones elipsoidales.

Fórmulas para distancia [ editar ]

La conversión de la distancia de la regla en el mapa de Mercator a la distancia verdadera ( gran círculo ) en la esfera es sencilla a lo largo del ecuador, pero en ningún otro lugar. Un problema es la variación de la escala con la latitud, y otro es que las líneas rectas en el mapa ( líneas de movimiento ), distintas de los meridianos o el ecuador, no corresponden a grandes círculos.

Mercator entendió claramente la distinción entre la distancia de rumbo (navegación) y la distancia de gran círculo (verdadero). (Vea Leyenda 12 en el mapa de 1569). Destacó que la distancia de la línea de rumbo es una aproximación aceptable para la distancia de círculo grande real para recorridos de corta o moderada distancia, particularmente en latitudes más bajas. Incluso cuantifica su enunciado: "Cuando las distancias del gran círculo que deben medirse cerca del ecuador no superan los 20 grados de un gran círculo, o 15 grados cerca de España y Francia, o 8 e incluso 10 grados en las partes norteñas. es conveniente utilizar distancias de línea de rumbo ".

Para una regla de medición de una línea corta , con el punto medio en la latitud  φ , donde el factor de escala es k  = sec  φ  =  1/cos  φ :

Distancia real = distancia de rumbo distance distancia de la regla × cos  φ / RF. (líneas cortas)

Con un radio y una circunferencia de círculo grande igual a 6,371 km y 40,030 km, respectivamente, un RF de 1/300M , para el cual R  = 2,12 cm y W  = 13,34 cm, implica que una regla de 3 mm. en cualquier dirección desde un punto en el ecuador corresponde a aproximadamente 900 km. Las distancias correspondientes para las latitudes 20 °, 40 °, 60 ° y 80 ° son 846 km, 689 km, 450 km y 156 km respectivamente.

Las distancias más largas requieren diversos enfoques.

En el ecuador [ editar ]

La escala es la unidad en el ecuador (para una proyección no secante). Por lo tanto, interpretar las medidas de la regla en el ecuador es simple:

Distancia verdadera = distancia de la regla / RF (ecuador)

Para el modelo anterior, con RF =  1/300M , 1 cm corresponde a 3,000 km.

En otros paralelos [ editar ]

En cualquier otro paralelo el factor de escala es sec φ para que

Distancia paralela = distancia de la regla × cos  φ / RF (paralelo).

Para el modelo anterior, 1 cm corresponde a 1,500 km a una latitud de 60 °.

Esta no es la distancia más corta entre los puntos finales elegidos en el paralelo porque un paralelo no es un gran círculo. La diferencia es pequeña para distancias cortas, pero aumenta a medida que λ , la separación longitudinal, aumenta. Para dos puntos, A y B, separados por 10 ° de longitud en el paralelo a 60 °, la distancia a lo largo del paralelo es aproximadamente 0,5 km mayor que la distancia del gran círculo. (La distancia AB a lo largo del paralelo es ( a  cos  φ )  λ . La longitud del acorde AB es 2 ( a  cos  φ ) sin  λ/2. Este acorde subtiende un ángulo en el centro igual a 2arcsin (cos  φ  sin  λ/2) y la gran distancia circular entre A y B es 2 una  arcosina (cos  φ  sin  λ/2 ). En el caso extremo en que la separación longitudinal es de 180 °, la distancia a lo largo del paralelo es la mitad de la circunferencia de ese paralelo. ; Es decir, 10,007.5 km. Por otro lado, la geodésica entre estos puntos es un arco de gran círculo a través del polo que subtiende un ángulo de 60 ° en el centro: la longitud de este arco es una sexta parte de la circunferencia del gran círculo, aproximadamente 6.672 km. La diferencia es de 3,338 km, por lo que la distancia de la regla medida desde el mapa es bastante engañosa incluso después de corregir la variación de latitud del factor de escala.

En un meridiano [ editar ]

Un meridiano del mapa es un gran círculo en el globo terráqueo, pero la variación de escala continua significa que la medición de la regla por sí sola no puede proporcionar la distancia real entre los puntos distantes del meridiano. Sin embargo, si el mapa está marcado con una escala de latitud precisa y bien espaciada desde la cual se puede leer directamente la latitud, como es el caso del mapa del mundo de Mercator 1569 (hojas 3, 9, 15) y todas las cartas náuticas posteriores, el meridiano la distancia entre dos latitudes φ ₁ y φ ₂ es simplemente

$${\ displaystyle m_ {12} = a | \ varphi _ {1} - \ varphi _ {2} |.}

Si las latitudes de los puntos finales no se pueden determinar con confianza, se pueden encontrar en cambio mediante el cálculo de la distancia de la regla. Al llamar a la regla las distancias de los puntos finales en el meridiano del mapa según se mide desde el ecuador y ₁ y y ₂ , la verdadera distancia entre estos puntos en la esfera se obtiene utilizando cualquiera de las fórmulas inversas de Mercator:

$${\ displaystyle m_ {12} = a \ left | \ tan ^ {- 1} \ left [\ sinh \ left ({\ frac {y_ {1}} {R}} \ derecha) \ right] - \ tan ^ {-1} \ left [\ sinh \ left ({\ frac {y_ {2}} {R}} \ right) \ right] \ right |,}

donde R puede calcularse a partir del ancho W del mapa mediante R  =  W/2 π . Por ejemplo, en un mapa con R  = 1, los valores de y  = 0, 1, 2, 3 corresponden a latitudes de φ  = 0 °, 50 °, 75 °, 84 ° y, por lo tanto, los intervalos sucesivos de 1 cm en el mapa Corresponde a intervalos de latitud en el globo terráqueo de 50 °, 25 °, 9 ° y distancias de 5,560 km, 2,780 km y 1,000 km sobre la Tierra.

En una rueca [ editar ]

Una línea recta en el mapa de Mercator en el ángulo α a los meridianos es una línea de rumbo . Cuando α  =  π/2 o 3 π/2 el rumor corresponde a uno de los paralelos; Sólo uno, el ecuador, es un gran círculo. Cuando α  = 0 o πcorresponde a un gran círculo meridiano (si se continúa alrededor de la Tierra). Para todos los demás valores, es una espiral de polo a polo en el globo que intersecta todos los meridianos en el mismo ángulo, y por lo tanto no es un gran círculo. ^[18] Esta sección discute solo el último de estos casos.

Si α no es ni 0 ni π , la figura anterior de los elementos infinitesimales muestra que la longitud de una línea de trazo infinitesimal en la esfera entre latitudes φ ; y φ  +  δφ es un  seg  α  δφ . Como α es constante en el rumbo, esta expresión se puede integrar para dar, para líneas de rumbo finitas en la Tierra:

$${\ displaystyle r_ {12} = a \ sec \ alpha \, | \ varphi _ {1} - \ varphi _ {2} | = a \, \ sec \ alpha \; \ Delta \ varphi.}

Una vez más, si Δ φ puede leerse directamente desde una escala de latitud precisa en el mapa, entonces la distancia de rumbo entre los puntos del mapa con latitudes φ ₁ y φ ₂ viene dada por lo anterior. Si no hay tal escala, entonces la regla distancia entre los puntos finales y el ecuador, y ₁ y y ₂ , da el resultado a través de una fórmula inversa:

$${\ displaystyle r_ {12} = a \ sec \ alpha \ left | \ tan ^ {- 1} \ sinh \ left ({\ frac {y_ {1}} {R}} \ right) - \ tan ^ {- 1} \ sinh \ left ({\ frac {y_ {2}} {R}} \ right) \ right |.}

Estas fórmulas proporcionan distancias de rumbo en la esfera que pueden diferir mucho de las distancias reales cuya determinación requiere cálculos más sofisticados.