En la cartografía , la cilíndrica proyección de áreas iguales es una familia de cilíndricas , de áreas iguales proyecciones de mapas .
Proyecciones cilíndricas [ editar ]
El término "proyección cilíndrica normal" se usa para referirse a cualquier proyección en la cual los meridianos se asignan a líneas verticales equidistantes y los círculos de latitud se asignan a líneas horizontales (o, mutatis mutandis , más generalmente, se asignan líneas radiales desde un punto fijo a líneas paralelas igualmente espaciadas y círculos concéntricos a su alrededor se mapean a líneas perpendiculares).
El mapeo de meridianos a líneas verticales puede visualizarse imaginando un cilindro (cuyo eje coincide con el eje de rotación de la Tierra) envuelto alrededor de la Tierra y luego proyectándose sobre el cilindro, y posteriormente desplegando el cilindro.
Por la geometría de su construcción, las proyecciones cilíndricas se extienden a distancias este-oeste. La cantidad de estiramiento es la misma en cualquier latitud elegida en todas las proyecciones cilíndricas, y está dada por la secante de la latitud como un múltiplo de la escala del ecuador. Las diversas proyecciones cilíndricas se distinguen entre sí únicamente por su estiramiento norte-sur (donde la latitud viene dada por φ ):
Las únicas proyecciones cilíndricas que preservan el área tienen una compresión de norte a sur, precisamente la recíproca del estiramiento este-oeste ( cos φ ): cilíndrica de igual área (con muchas especializaciones nombradas como la ortografía de Gall-Peters o Gall, Behrmann y la cilíndrica de Lambert -area ). Esto divide las distancias de norte a sur por un factor igual a la secante de la latitud, preservando el área pero distorsionando las formas.
Cualquier mapa cilíndrico de áreas iguales en particular tiene un par de latitudes idénticas de signo opuesto (o también el ecuador) en el que la escala este-oeste coincide con la escala norte-sur.
Descripción [ editar ]
Fórmulas [ editar ]
Todas las proyecciones cilíndricas de áreas iguales utilizan la fórmula:
donde λ es la longitud, λ 0 es el meridiano central, φ es la latitud y φ 0 es la latitud estándar, [1] todo expresado en radianes.
Algunos cartógrafos prefieren trabajar en grados, en lugar de radianes, y usan la fórmula equivalente:
Fórmula simplificada [ editar ]
Al eliminar la conversión de unidades y la escala uniforme, las fórmulas se pueden escribir:
Por lo tanto, la esfera se asigna a un cilindro vertical estirado. El factor de estiramiento S es lo que distingue las variaciones de la proyección cilíndrica de áreas iguales.
Discusión [ editar ]
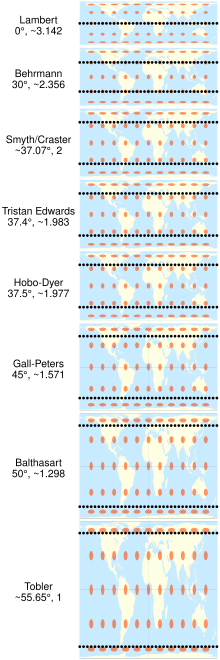
Las diversas especializaciones de la proyección cilíndrica de áreas iguales difieren solo en la relación entre el eje vertical y el horizontal. Esta relación determina el paralelo estándar de la proyección, que es el paralelo en el que no hay distorsión ya lo largo de la cual las distancias coinciden con la escala establecida. Siempre hay dos paralelos estándar en la proyección cilíndrica de áreas iguales, cada una a la misma distancia al norte y al sur del ecuador. Los paralelos estándar de Gall-Peters son 45 ° N y 45 ° S. Se han descrito, promovido o nombrado de otra forma varias otras especializaciones de cilindros cilíndricos de igual área. [2] [3] [4] [5] [6]
| Proyección | Imagen | Creador (año) | Estándar paralelos norte y sur | Relación de aspecto ancho-alto |
|---|---|---|---|---|
| Cilindro de igual área (proyección de base para todos los demás). | φ 0 | π (cos φ 0 ) 2 | ||
| Lambert | Johann Heinrich Lambert(1772) | Ecuador (0 °) | π ≈ 3.142 | |
| Behrmann |  | Walter Behrmann (1910) | 30 ° | 3 π4 ≈ 2.356 |
| Smyth igual superficie = Craster rectangular | Charles Piazzi Smyth(1870) | ≈ 37 ° 04′17 ″ | 2 | |
| Trystan Edwards | Trystan Edwards (1953) | 37 ° 24 ′ | 1.983 | |
| Hobo – Dyer | 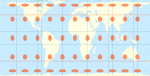 | Mick Dyer (2002) | 37 ° 30 ′ | ≈ 1.977 |
| Gall – Peters = Gall ortográfico = Peters | 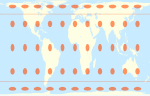 | James Gall (1855) Promovido por Arno Peters como su propio invento (1967) | 45 ° | π2 ≈ 1.571 |
| Balthasart | M. Balthasart (1935) | 50 ° | 1.298 | |
| El mundo de Tobler en una plaza. | Waldo Tobler (1986) | ≈ 55 ° 39′14 ″ | 1 |
Historia [ editar ]
La invención de la proyección cilíndrica de igual área de Lambert se atribuye al matemático suizo Johann Heinrich Lambert en 1772. [7] Las variaciones aparecieron a lo largo de los años por inventores que estiraron la altura del Lambert y comprimieron el ancho proporcionalmente en varias proporciones. Ver tabla de especializaciones nombradas .
La proyección hiperelíptica de Tobler , descrita por primera vez por Tobler en 1973, es una generalización adicional de la familia cilíndrica de igual área.
La proyección HEALPix es una combinación híbrida de igual área de: la proyección cilíndrica de igual área de Lambert, para las regiones ecuatoriales de la esfera; y una proyección de Collignon interrumpida, para las regiones polares.
El mapa Dymaxion o Fuller es una proyección de un mapa del mundo sobre la superficie de un icosaedro , que puede desplegarse y aplanarse en dos dimensiones. El mapa plano está muy interrumpido para preservar formas y tamaños.
La proyección fue inventada por Buckminster Fuller . La edición de la revista Life del 1 de marzo de 1943 incluyó un ensayo fotográfico titulado "La vida presenta R. El mundo de Dymaxion de Buckminster Fuller". El artículo incluyó varios ejemplos de su uso junto con una sección extraíble que podría ser ensamblada como una "aproximación tridimensional de un globo o como un mapa plano, con el cual el mundo puede ser unido y reorganizado para iluminar objetos especiales. Aspectos de su geografía ". [1] Fuller solicitó una patente en los Estados Unidos en febrero de 1944, la solicitud de patente muestra una proyección en un cuboctaedro . La patente fue emitida en enero de 1946. [2]
La versión de 1954 publicada por Fuller, hecha con el co-cartógrafo Shoji Sadao , el Mapa Mundial de Airocean , usó un icosaedro modificado pero en su mayoría regular como la base para la proyección, que es la versión más comúnmente mencionada en la actualidad. Esta versión describe los continentes de la Tierra como "una isla", o masas de tierra casi contiguas .
La proyección Dymaxion está diseñada solo para representaciones de todo el mundo. No es una proyección gnomónica , en la que los datos globales se expanden desde el punto central de una faceta tangente hacia los bordes. En su lugar, cada borde de triángulo del mapa Dymaxion coincide con la escala de un gran círculo parcial en un globo correspondiente, y otros puntos dentro de cada faceta se reducen hacia su centro, en lugar de agrandarse hacia las periferias. [3]
Propiedades [ editar ]
Fuller afirmó que su mapa tenía varias ventajas sobre otras proyecciones para los mapas mundiales.
Tiene menos distorsión del tamaño relativo de las áreas, especialmente cuando se compara con la proyección de Mercator ; y menos distorsión de las formas de las áreas, especialmente cuando se compara con la proyección de Gall-Peters . Otras proyecciones de compromiso intentan una compensación similar.
Más inusualmente, el mapa Dymaxion no tiene ningún "camino hacia arriba". Fuller argumentó que en el universo no hay "arriba" ni "abajo", o "norte" y "sur": solo "dentro" y "fuera". [4] Las fuerzas gravitacionales de las estrellas y los planetas crearon "en", que significa "hacia el centro gravitatorio", y "hacia afuera", que significa "lejos del centro gravitacional". Él atribuyó la presentación norte-arriba-arriba / sur-abajo-inferior de la mayoría de los otros mapas mundiales al sesgo cultural .
Fuller pretendía que el mapa se desplegara de diferentes maneras para enfatizar diferentes aspectos del mundo. [5] Alseparar las caras triangulares del icosaedro de una manera, se obtiene una red icosaédrica que muestra una masa de tierra casi contigua que comprende todos los continentes de la Tierra, no grupos de continentes divididos por océanos. La separación de los sólidos de una manera diferente presenta una visión del mundo dominada por océanos conectados rodeados de tierra.
Mostrar a los continentes como "una isla de la isla" también ayudó a Fuller a explicar, en su libro Critical Path , los viajes de los primeros navegantes, que utilizaron los vientos predominantes para circunnavegar esta isla del mundo.
Sin embargo, el mapa Dymaxion también puede resultar difícil de usar. Es, por ejemplo, confuso describir las cuatro direcciones cardinales y localizar coordenadas geográficas . La forma incómoda del mapa puede ser contraintuitiva para la mayoría de las personas que intentan usarlo. Por ejemplo, trazar un camino de la India a Chile puede ser confuso. Dependiendo de cómo se proyecte el mapa, las masas de tierra y los océanos a menudo se dividen en varias partes.
Impacto [ editar ]
Una pintura de Jasper Johns de 1967 , Map (basada en Dymaxion Airocean World de Buckminster Fuller) , que muestra un mapa de Dymaxion, cuelga en la colección permanente del Museo Ludwig en Colonia . [6] [7]
The World Game , un juego de simulación colaborativa en el que los jugadores intentan resolver problemas mundiales, [8] [9] se juega en un mapa Dymaxion de 70 x 35 pies. [10]
En 2013, para conmemorar el 70 aniversario de la publicación del mapa Dymaxion en la revista Life , el Instituto Buckminster Fuller anunció el "Dymax Redux", un concurso para diseñadores gráficos y artistas visuales para volver a imaginar el mapa Dymaxion. [11] [12] El concurso recibió más de 300 entradas de 42 países.











No hay comentarios:
Publicar un comentario